4. Линейные двоичные блочные коды

Линейными называют такие двоичные коды, в которых множество всех разрешенных блоков является линейным пространством относительно операции поразрядного сложения по модулю 2. Чтобы разрешенные блоки были линейным пространством, они должны содержать нулевой блок, т.е. блок, состоящий из n нулей, должен быть разрешенным, а сумма (поразрядная по модулю 2) любых разрешенных блоков должна быть также разрешенным блоком. Линейные коды называют также групповыми. Двоичный линейный код можно построить следующим образом. Среди всех 2ⁿ последовательностей кодовых символов можно выбрать различными способами n линейно-независимых. В частности, ими могут быть элементы, образующие ортогональный базис. Выберем из них k любых линейно-независимых блоков, которые обозначим ₁, ₂,..., _л (k < n), и образуем все линейные комбинации вида:

, (15)

где _il принимает значения 0 или 1, а суммирование - поразрядное по модулю 2. Множество {b_i} этих комбинаций образует линейное пространство, содержащее 2^k блоков, т.е. линейный код. Множество {b_i} содержит нулевой элемент, получающийся, когда все _il = 0 (l = 1,...k). Сумма любых двух элементов 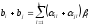представляет собой также элемент этого множества, поскольку_il + _jl принимает значения 0 или 1. Если записать k линейно-независимых блоков, используемых для построения линейного кода, в виде k строк, то получится матрица размером nk, которую называют порождающей или производящей матрицей кода G.

В общем случае производящая матрица двоичного кода записывается в виде:

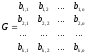(16)

b_ij - двоичный символ (0 или 1), находящийся в j-м разряде i-го кодового слова _i, входящего в выбранный базис.

Полученный таким образом код, содержащий 2^k блоков длиной n, обозначают (n,k). При заданных n и k существует много различных (n,k) - кодов с различными кодовыми расстояниями d, определяемых различными порождающими матрицами. Все они имеют избыточность Н_k = 1 - k/n или относительную скорость R_k = k/n.

Если две порождающие матрицы различаются только порядком расположения столбцов, то определяемые ими коды являются изоморфными пространствами. Такие коды называются эквивалентными. Они имеют одинаковые кодовые расстояния между соответствующими парами кодовых векторов и, следовательно, одинаковые способности обнаруживать и исправлять ошибки.

Чаще всего применяют систематические линейные коды, которые строят следующим образом. Сначала строится простой код длиной k, т.е. множество всех k -последовательностей двоичных символов, называемых информационными. Затем каждой из этих последовательностей приписывается r = n - k проверочных символов, которые получаются в результате некоторых линейных операций над информационными символами.

Простейший систематически код (n,n - 1) строится добавлением к комбинации из n - 1 информационных символов одного проверочного, равного сумме всех информационных символов по модулю 2.Легко видеть, что эта сумма равна нулю, если среди информационных символов содержится четное число единиц, и равна 1, если число единиц среди информационных символов нечетное. После добавления проверочного символа образуются кодовые комбинации, содержащие только четное количество единиц, т.е. комбинации с четным весом.

Такой код (n,n - 1) имеет d = 2, поскольку две различные кодовые комбинации, содержащие по четному числу единиц не могут различаться в одном разряде. Применяя этот код в схеме декодирования с обнаружением ошибок, можно обнаруживать все ошибки нечетной кратности. Для этого достаточно подсчитать число единиц в принятой комбинации и проверить, является ли оно четным. Такой код называют кодом одной проверки на четность.

Обозначим b_i символ кода (0 или 1), стоящий на i-м месте в кодовой комбинации. Тогда для систематического (n,k) - кода общего вида получаем следующее правило построения комбинаций (b₁,..., b_k, b_k+1, b_n); символы b₁,..., b_k выбирают в соответствии с передаваемой информацией, а b_i при i > k определяют так, чтобы удовлетворялось условие:

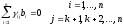, (17)

где _ij - коэффициенты (0 или 1), характеризующие данный код. Если набор всех коэффициентов _ij собрать в таблицу (матрицу), то получим так называемую проверочную матрицу кода Н размерности n(n - k):

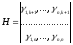(18)

Для рассмотренного примера кода (n,n - 1) с четным весом поверочная матрица вырождается в строку длиной n: , а порождающая матрица имеет вид:

(19)

Рассмотрим другой пример систематического кода - кода (7,4), заданного порождающей матрицей:

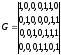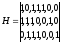(20). Или проверочной матрицей: (21)

Этот код имеет d = 3 и позволяет обнаруживать все одиночные и двойные ошибки или исправлять (по алгоритму Хэмминга) все одиночные ошибки.

Проверочная матрица может служить порождающей для другого линейного кода (n,n - k), называемого двойственным. Так, например матрица (21) является порождающей матрицей кода (7,3), имеющего d = 4. Матрица (20) является проверочной для этого кода.

Преимуществом линейных, в частности систематических, кодов является то, что в кодере и декодере не нужно хранить список из 2^k, блоков. Вместо этого достаточно хранить, например, n - k строк проверочной матрицы и при декодировании проверять выполнение n - k равенств (17). Так, например, при коде (100,50) нужно хранить 50 строк по 100 символов, а не 10¹⁷, как при табличном кодировании, и проверять 50 равенств, вместо перебора 10¹⁵ расстояний.

Обнаруживать и исправлять ошибки при систематическом коде можно следующим образом. В режиме обнаружения ошибок проверяют выполнение равенств (17) и если хотя бы одно из них не выполнено, принятый блок бракуют, как ошибочный. В режиме исправления ошибки, после проверки равенства 917) строится последовательность c(c₁, c₂,..., c_n-k), называемая синдромом, где c_j(j = 1,..., n - k) - двоичный символ, равный нулю, если j-e равенство в (17) выполнено, и единице, если оно не выполнено (термин “синдром” заимствован из медицины, где он обозначает сочетание симптомов, характерных для определенного заболевания. В данном случае синдром представляет сочетание результатов проверок равенств (17), характерное для определенной конфигурации ошибок).

Нулевой синдром указывает на то, что все проверки выполнены, т.е. принятый блок является разрешенным. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется. Так, например, для рассмотренного кода (7,4) в таблице представим ненулевые синдромы и соответствующие конфигурации ошибок.:

Синдром	001	010	011	100	101	110	111
Конфиг. ошибок	0000001	0000010	0100000	0000100	0001000	1000000	0010000

Из этого примера видно, что при декодировании систематического кода не требуется перебирать таблицу, содержащую 2^k кодовых комбинаций, и производить n - k сравнений. Декодер должен перебрать таблицу 2^{n - k} строк.

К наиболее простым двоичным систематическим кодам относят коды Хэмминга с d = 3. Для любого натурального числа r существует код Хэмминга при n = 2^r - 1 и k = n - r.