П2.3. Дифференциальные операции второго порядка
Результат дифференцирования скалярных и векторных полей – одна скалярная функция (дивергенция) и две векторные (градиент скалярного поля и ротор векторного). Второе применение операции дифференцирования даст одну векторную функцию (от скалярной) и по две скалярных и векторных функций от векторных. Таким образом, можно составить пять дифференциальных операторов второго порядка:
grad div 
,
rot grad U, rot rot
,
div grad U, div rot 
.
Число
независимых операций можно сократить.
Два первых оператора – тождественные
нули. Это rot grad U и
div rot 
.
Покажем это в прямоугольной системе
координат, пользуясь векторными и
дифференциальными свойствами вектора
.
rot grad U = 
U
= 0, (П2.22)
как векторное произведение двух параллельных векторов.
div rot
= 
[
]
= 0, (П2.23)
как скалярное произведение двух взаимно перпендикулярных векторов.
Рассмотрим оставшиеся три операции.
div grad U = 
U
= 
U
= U.
(П2.24)
Операция получила название оператора Лапласа.
rot rot 
=
=
(
)
–
(
)
= 
(
)
–
=
= grad div 
– 
.
(П2.25)
Рассматривать
оставшуюся операцию не нужно. Она
вошла в выражение для rotrot
.
Итак,
операции дифференцирования второго
порядка свелись к лапласиану от скалярной
и векторной величины и rotrot
.
Запишем лапласиан скалярного поля в обобщенных координатах:
.
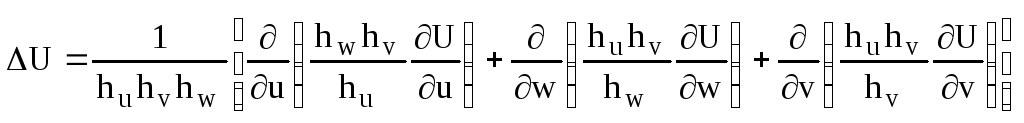В различных ортогональных системах координат лапласиан скалярной величины выглядит так:
; (П2.26)
;
(П2.27)
(П2.28)
Лапласиан векторного поля в обобщенной ортогональной системе координат имеет весьма сложную форму. Выражение для лапласиана приведено у Федорова. Здесь приведем выражение для лапласиана векторного поля в прямоугольной системе координат.
.
(П2.29)
П3. Интегральные теоремы, используемые при анализе электромагнитных полей
При анализе электромагнитных полей используют интегралы по объему и по поверхности, ограничивающей этот объем. Если величина, изменяющаяся в объеме, например, электрический заряд, может изменяться только за счет того, что изменяется поток этой величины из объема, то справедлива теорема Остроградского-Гаусса,которая связывает интеграл от дивергенции поля в замкнутом объеме и интеграл по поверхности, ограничивающей этот объем.
Эта теорема утверждает, что поток векторного поля через замкнутую поверхность равен сумме всех источников полей, порождаемых в этом объеме. Поле в объеме не может пропасть бесследно. Если оно изменяется, то это изменение происходит либо за счет того, что источники порождают дополнительное поле, либо за счет того, что поле просачивается через поверхность, ограничивающую объем.
(П2.30)
Аналогичная связь между интегралом от ротора векторного поля по некоторой поверхности и интегралом по кривой, ограничивающей эту поверхность, дает теорема Стокса.
По существу ротор векторного поля характеризует вращательные свойства векторного поля. Так, например, для равномерного вращения ротор линейной скорости равен удвоенной угловой скорости. Суммарное вращательное свойство поля, пронизывающего поверхность, описывается циркуляцией поля по контуру, ограничивающему эту поверхность.
(2.31)
Теорема Грина связывает свойства двух скалярных полей в объеме и на поверхности, ограничивающей этот объем.
.
(2.32)