П2.2. Дифференциальные операции первого порядка

Рассмотрим некоторые соотношения векторного анализа, которые необходимы при изучении электромагнитных волн. Пусть задана некоторая функция одного аргумента. Скорость изменения функции описывается с помощью производной. Производная находится дифференцированием заданной функции. Дифференциальные операции определены не только для функции одной переменной, но и для скалярных и векторных полей. Для скалярного поля обычно вводят одну дифференциальную операцию первого порядка – градиент. Для векторных полей две операции – дивергенция и ротор.

Градиент скалярного поляэто вектор, направленный по нормали к поверхности равного уровня в сторону возрастания функции и численно равный скорости изменения функции по этому направлению.

. (П2.1)

Черточку над символом градиента обычно не ставят. Градиент в обобщенной ортогональной системе координат u, v, wзаписывается в виде:

. (П2.2)

Воспользуемся таблицей коэффициентов Ляме (см. таб. П1.1) и запишем градиент в различных системах координат.

, (П2.3)

, (П2.4)

. (П2.5)

Дивергенцией векторного поляназывают удельный поток этого вектора из объемаVчерез поверхностьS, ограничивающую этот объем, приV, стремящемся к нулю.

. (П2.6)

Дивергенция – это скаляр, описывающий источники поля. Если из рассматриваемой точки идет поток вектора , то в этой точке есть источник или сток этого вектора. В противном случае, какой поток вектора войдет через поверхность в объем, такой и выйдет и суммарный поток будет равен нулю.

Дивергенция в обобщенной ортогональной системе координат u, v, wзаписывается в виде:

.

Воспользуемся таблицей коэффициентов Ляме и запишем дивергенцию вектора в различных системах координат.

(П2.8)

(П2.9)

(П2.10)

Ротором векторного поля называют циркуляцию этого вектора по замкнутому контуруℓ, поделенную на величину площадиS, охваченной этим контуром при стремленииSк нулю. Ротор – векторная величина. Он направлен по нормали к поверхностиS.

(П2.11)

Запишем проекции ротора векторана координатные оси в обобщенной системе координат.

;

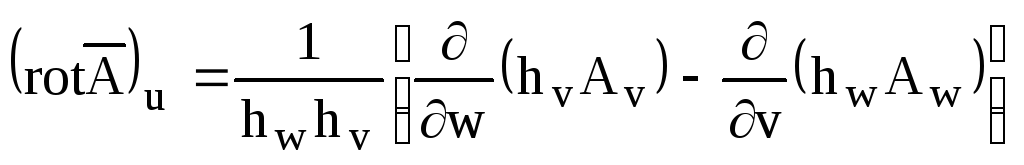
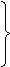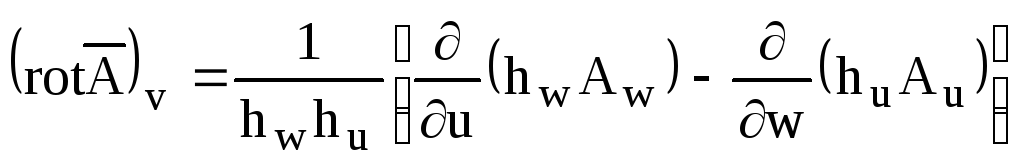; (П2.12)

.

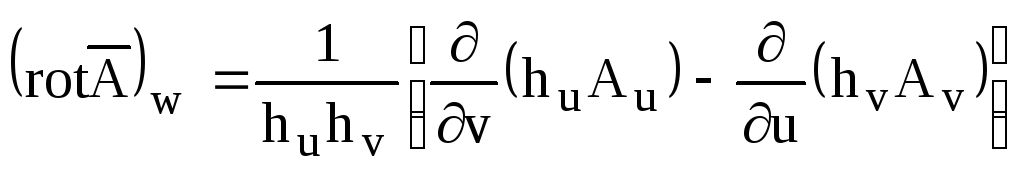Воспользуемся таблицей коэффициентов Ляме и запишем проекции ротора вектора в различных системах координат.

;;

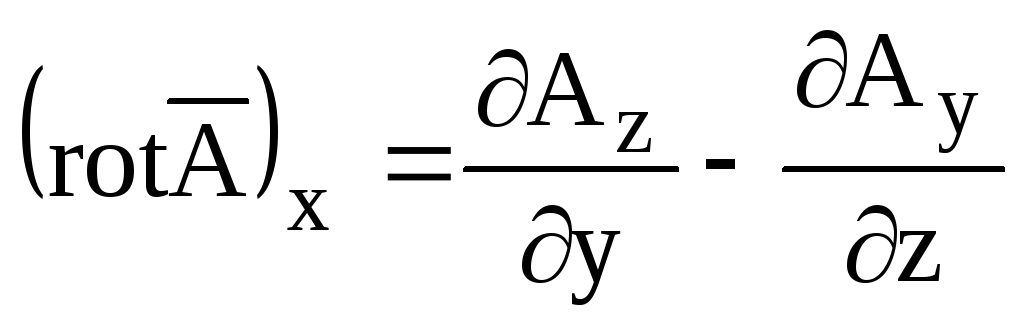
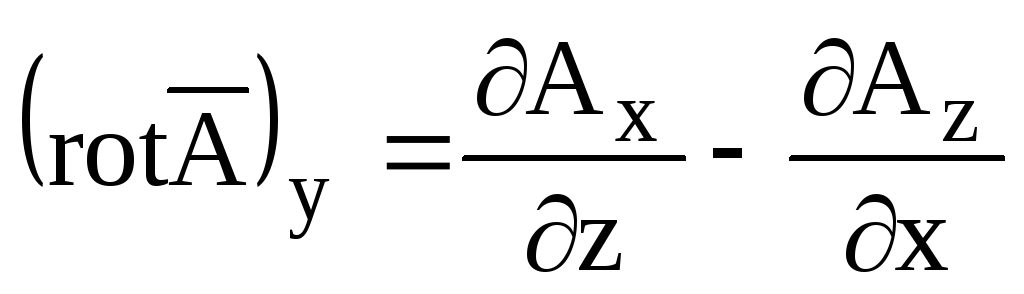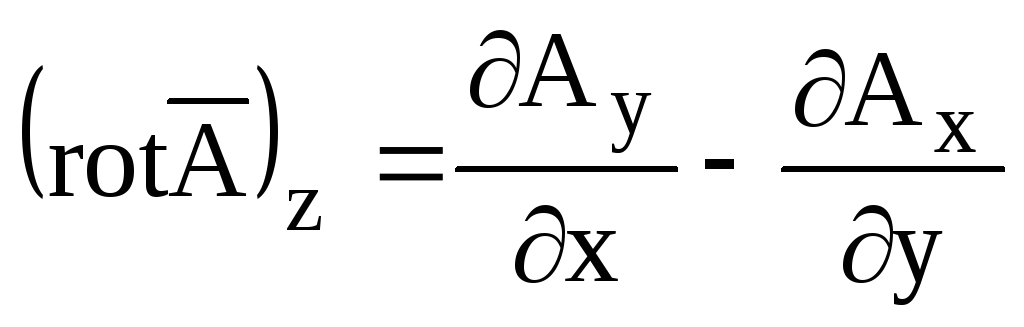. (П2.13)

;;

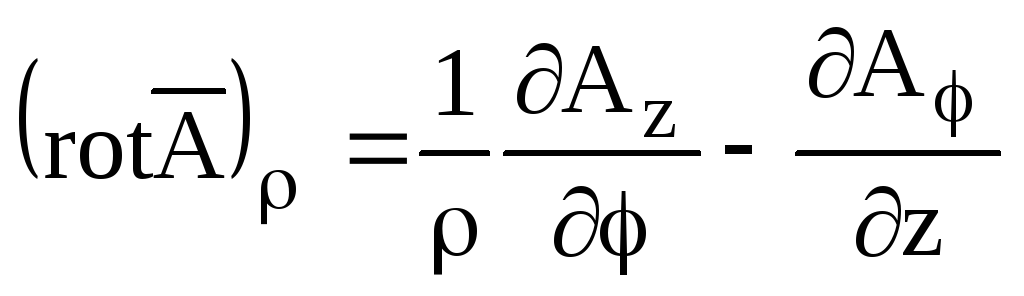
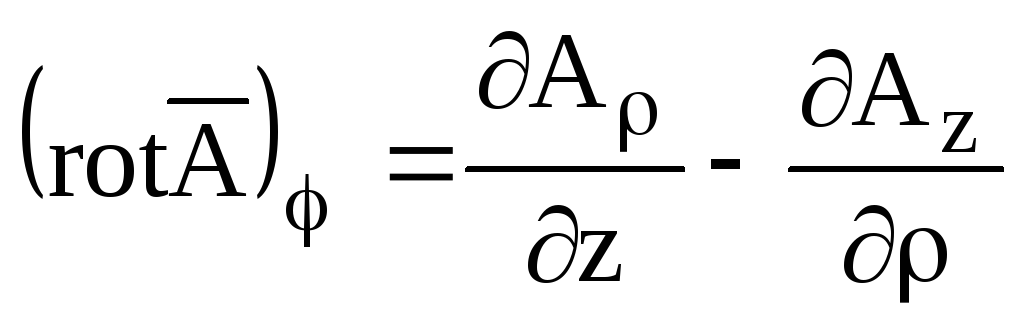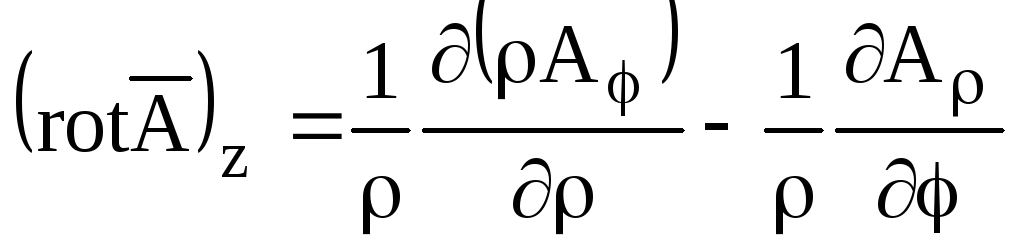. (П2.14)

;

;

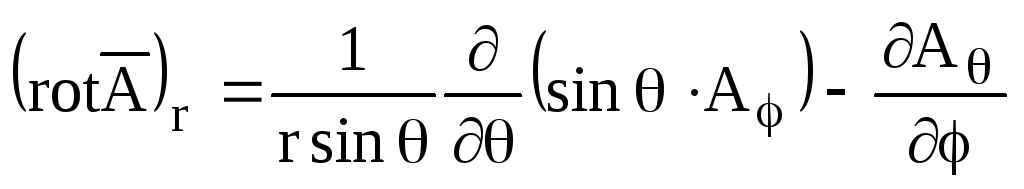
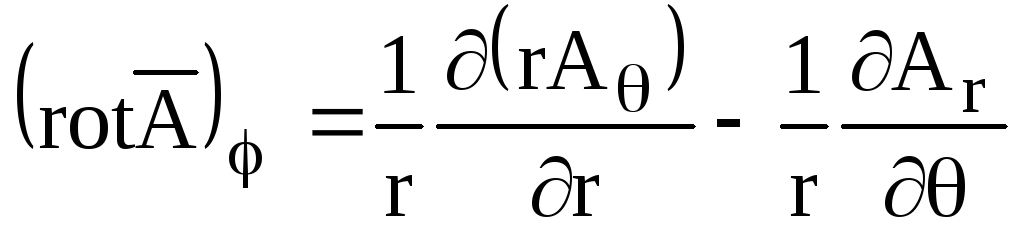
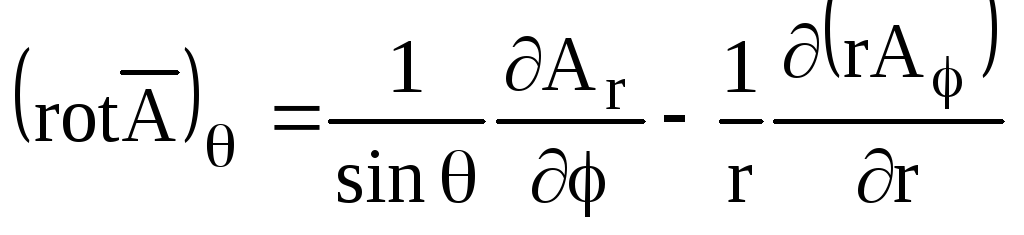. (П2.15)

В прямоугольной системе координат дифференциальные операции над полями принято представлять с помощью векторного оператора

. (П2.16)

Оказывается, что

grad U =U, div = (), rot= [].

В этих выражениях операторучаствует и как обычный вектор, и как оператор, выполняющий операции дифференцирования. Пользуясь, можно получить правила выполнения дифференциальных операций первого порядка над произведениями полей. Найдем, например, дивергенцию векторного произведения двух векторов.

. (П2.17)

Проведенные операции можно прокомментировать так. Сначала используются дифференциальные свойства оператора . Берется производная от произведения. Сомножители нельзя произвольно переставлять, так как в векторном произведении при перестановке сомножителей изменяется знак. Поэтому, сохраняя прежний порядок сомножителей, мы отмечаем символом «дуга» тот сомножитель, на который действует дифференциальный оператор. В одном из случаев дифференциальный оператор оказывается справа от сомножителя, на который он воздействует. Нужно переставить их местами. Так и делаем, но не забываем, что при этом знак произведения изменится. Получив окончательное выражение, заменяем операторградиентом, если он воздействует на скаляр; дивергенцией, если он участвует в скалярном произведении и ротором, если он участвует в векторном произведении.

Запишем еще ряд равенств, часто используемых при анализе электромагнитных полей.

grad (U) =(U) == grad U + U grad . (П2.18)

. (П2.19)

(П2.20)

(П2.21)