Переходные процессы при некорректных коммутациях

К числу задач с некорректными коммутациями относят задачи, в которых нарушаются основные законы коммутации:

u_C(0-)=u_C(0+); i_L(0-)=i_L(0+).

Такое название является чисто условным и в целом ряде практически важных задач указанное явление имеет место.

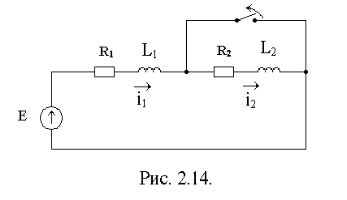
Рассмотрим цепь, представленную на рис. 2.14. Очевидно, что в данной цепи не может выполняться закон непрерывности тока в индуктивности, поскольку i₁(0+)=i₂(0+)=i(0+), а i₁(0-)¹i₂(0-)

Дифференциальное уравнение цепи для t ñ 0:

Его решение

(2.10)

Постоянная интегрирования A определяется по начальному значению тока после коммутации i(0+), которое в данном случае мы не можем определить, используя закон коммутации для ветви с индуктивностью, на основании выше сказанного. В нашем случае необходим другой подход. Рассмотрим его.

Дифференциальное уравнение цепи, запишем в виде:

В предположении, что коммутация происходит мгновенно (Dt®0), напряжение на каждой из индуктивностей неограниченно возрастает. При этом сумма должна оставаться конечной, т.к. все остальные слагаемые, входящие в уравнение, заведомо конечны.

Каждую из производных di_n/dt можно представить как предел отношения Di_n/Dt при Dt®0. Но Di₁=i₁(0+)-i₁(0-) и Di₂=i₂(0+)-i₂(0-). Поэтому:

.

Эта сумма остается конечной при Dt®0 только при условии, что

или

.

Последнее равенство выражает закон сохранения магнитного потокосцепления, представляющий обобщение закона коммутации: суммарное магнитное потокосцепление катушек индуктивности в момент коммутации не может измениться скачком.

Используем данный закон для определения i(0+).

До коммутации:

После коммутации:

Следовательно:

Подставив данное выражение в выражение (2.10), получим

Окончательно:

Пример некорректной коммутации в цепях с емкостными элементами представлен на рис. 2.15.

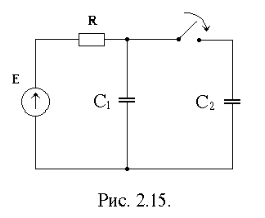
Действительно, начальные условия для двух емкостей c учетом закона коммутации:

Но сразу после коммутации напряжение на емкостях должно быть одинаковым, т.е.

В общем случае, при разных начальных напряжениях на емкостях, противоречие полученных равенств очевидно,.т.е. в данной цепи закон коммутации для емкостей не выполняется. Это объясняется тем, что при выводе законов коммутации предполагалось, что величина мощности (ui) c которой энергия передается от одного элемента цепи к другому конечна. Но если сопротивление проводов, соединяющих емкости C₁ и C₂, стремится к нулю, то протекающий ток стремится к бесконечности, пока напряжения на емкостях не станут равными. Это значит, что к такой цепи закон коммутации не применим. Нужно исходить из более общих законов, не зависящих от того, остается ли мощность конечной.

Таким более общим законом является закон сохранения заряда: суммарный заряд емкостей в момент коммутации не может измениться скачком.

Математическая запись закона применительно к нашей цепи:

,

т.е. сумма зарядов, существовавших на емкостях до коммутации равна их общему заряду сразу после коммутации, когда обе емкости имеют одинаковое напряжение u_C(0+).

Алгоритм расчета переходных процессов при некорректных коммутациях в цепях с емкостями в целом остается без изменений. Единственное отличие состоит в том, что при нахождении начальных значений u_C1(0+)=u_C2(0+)=u_C(0+) необходимо исходить не из закона непрерывности напряжения на емкостях, а из более общего закона сохранения их суммарного заряда.

22