Переходные процессы при мгновенном изменении параметров цепи.

Пример электрической цепи с коммутацией подобного рода приведен на рис. 2.8.

Определим ток в индуктивности в переходном режиме. Для этого составим уравнения по законам Кирхгофа.

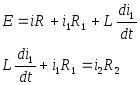
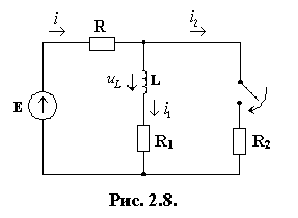
Из второго уравнения имеем:

Подставляя данное уравнение во второе уравнение исходной системы уравнений , с учетом первого, получим после соответствующих преобразований:

(25)

Решение для i₁ ищем в виде:

(2.6)

При t®µ i₁ =i_1ПР и , поскольку источником питания является источник постоянной э.д.с., а, следовательно, из уравнения (2.5) получим:

Решение для свободной составляющей тока:

_,

где p- корень характеристического уравнения

Отсюда

Постоянная интегрирования A определяется из уравнения (2.6.) для момента времени t=0₊ с учетом начальных условий и закона коммутации для ветвей с индуктивностью:

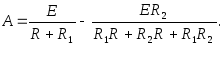
Переходные процессы в цепи с последовательно соединенными элементами r, l и c.

Пусть последовательно соединенные элементы R, L и C (рис. 2.9) включаются в цепь источника e(t).

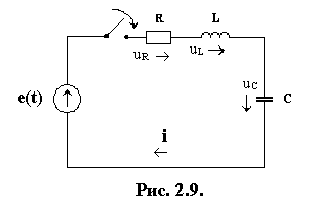
Дифференциальное уравнение цепи относительно тока:

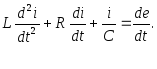
Решение ищем в виде

Характеристическое уравнение

Его корни

Следовательно

Общее решение

(2.7)

Поэтому

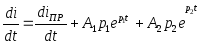(2.8)

Постоянные интегрирования А₁ и А₂ определим из начальных условий с учетом законов коммутации. При этом учтем, что

В результате получим

(2.9)

Принужденную составляющую тока и ее производную можно найти, если известен вид функции e(t). Поэтому полученная система уравнений позволяет определить постоянные интегрирования при заданных начальных условиях i(0-) и uC(0-).

Разряд конденсатора на rl цепь

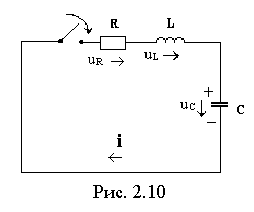
Пусть напряжение на конденсаторе в момент коммутации равноU0 , а положительные направления тока и напряжений на элементах цепи такие же как в предыдущем примере(рис. 2.10). В данном случае приложенное напряжение, а также ток установившегося режима ,равны нулю, т.е. e(t)=0 и i_ПР=0. Тогда из системы уравнений (2.9) получим:

,

откуда

Окончательно для тока имеем:

и ,соответственно, для напряжений на катушке и на конденсаторе получим:

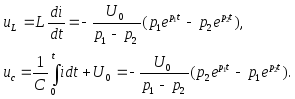
Последнее выражение получено с учетом того что

Характер процессов при разряде конденсатора зависит от характера корней характеристического уравнения.

Исследуем различные возможные случаи.

1) Корни характеристического уравнения вещественны, отрицательны и отличны друг от друга.

Это имеет место при условии . Так какp₁<0 и p₂<0 и, кроме того, êp₂ ê>êp₁ê, то при изменении t от 0 до µ разность всегда положительна. Следовательно, ток не меняет своего направления, т.е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называют апериодическим разрядом.

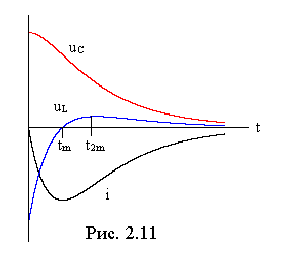
На рис. 2.11 изображены кривые i(t), u_C(t), и u_L(t). В интервале времени 0 < t< t_m ток по абсолютному значению возрастает и достигает максимума при . Значение t_m находится из условия , т.е. из условия. В интервале времениt_m < t < µ ток по абсолютному значению убывает, стремясь к нулю.

Напряжение на индуктивности достигает своего максимума U_{L max} при t=t_2m=2t_m, что находится из условия .

2) Корни характеристического уравнения вещественны, отрицательны и равны друг другу.

Данный случай, когда , имеет место при. При этом выражения для тока и напряжения становятся неопределенными из-за равенства нулю и числителя и знаменателя. Раскроем эти неопределенности по правилу Лопиталя, считая что p₁-переменная и стремится к p₂.

Получим:

Для напряжений соответственно получим:

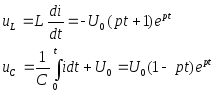
Характер процессов в этом случае не отличается от рассмотренного выше. Процесс также апериодический, причем данный случай является предельным случаем апериодического разряда, так как при дальнейшем уменьшении R ниже значения разряд становится колебательным.

3) Корни характеристического уравнения комплексные. Это имеет место при .

Введем обозначения:

Корни характеристического уравнения можем записать в виде

,

где угол лежит в пределах, так как

и .

Тогда выражение для тока примет вид

С учетом формулы Эйлера

получим

Для u_L и u_C :

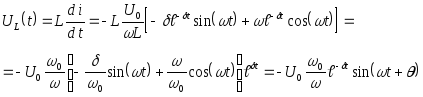
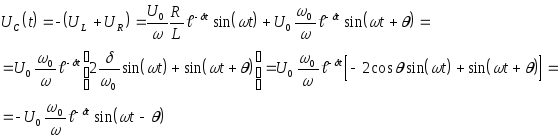
Кривые i, u_L и u_C представлены на рис 2.12.

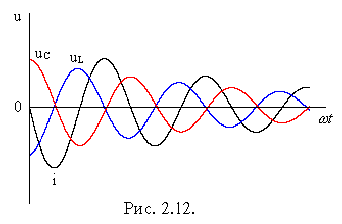
Из полученных выражений и кривых видно, что процесс в данном случае является колебательным. Амплитуда колебаний убывает по показательному закону, следовательно, в цепи совершаются затухающие колебания тока и напряжений. Угловая частота затухающих колебаний равна .Соответственно период затухающих колебаний определяется как. Быстроту затухания тока принято характеризовать так называемым декрементом колебаний равным отношению двух последующих амплитуд одного знака:,а также логарифмическим декрементом колебаний, равным .

В предельном случае R=0 и . В этом случае колебания будут незатухающими, так как энергия полей не рассеивается. Угловая частота незатухающих колебаний, как видим, равна резонансной частоте контура. Выражения для тока и напряжений принимают вид