15. Квадратурные формулы на основе интерполяций.

Пусть требуется вычислить интеграл:,(1)где-весовая функция ( абсолютно интегрируема нас весом(x))

Рассмотрим сначала случай.

Определение. Квадратурной формулой n-го порядка для интеграла (1) называется выражение вида:,(2)где- веса квадратурной формулы,- узлы ,(узел),-остаточный член квадратурной формулы. Начнем с рассмотрения простого примера.

Пример 1.Пусть ,- строго выпукла на этом отрезке,,().Заменимконстантой на. Как ее выбрать? (т.е. приблизить функцию полиномом нулевой степениQ₀(x)).1) Положим см. рисунок. Площадь-формула прямоугольника.

2) - что лучше?

3) Выберем таким образом, чтобы, причемmin в классе функций. Первый подход связан с приближением функции интерполяционным многочленом. Это наиболее простой путь получения квадратурных формул. Рассмотрим этот подход наиболее подробно. Положим, (3) где- многочлен Лагранжа, построенный по узлам, выбираемых пока произвольно. Как известно из теории интерполяции (Л-2), где (4)

(5)

- фундаментальные полиномы Лагранжа. Остаточный член интерполяционной формулы имеет вид (Л-2):,где

Из (3) и (4) (6)

Проинтегрируем формулу (6) по

Обозначим,(7)(8)

(7)-веса, (8)-остаточный член квадратурной формулы, интегралы в (7) легко вычисляются, как интегралы от полиномов. Рассмотрим некоторые частные случаи.

n=0 Нужна одна точка (узел) .Еслииспользуя формулы (5) и (7), получим формулу прямоугольников типа 1) из примера 1. Заметим, что исследование остаточного члена в виде (8) не совсем удобно, так как необходимо уточнить точку, которая определяется в соответствии с теоремой о среднем. Будем оценивать остаточный член по модулю:, (9) где.

Пример. Получить оценку остаточного члена для формулы прямоугольников.

Самостоятельно.Перейдем к выводу квадратурной формулы порядка 1.

n=1Узлы: . Согласно формулам (5), имеем

По формуле (7)

–формула трапеций(10)

Площадь под кривой y=f(x) приближается с помощью формулы - площадь трапеции.Геометрическая иллюстрация.

Оценим остаточный член формулы трапеций:

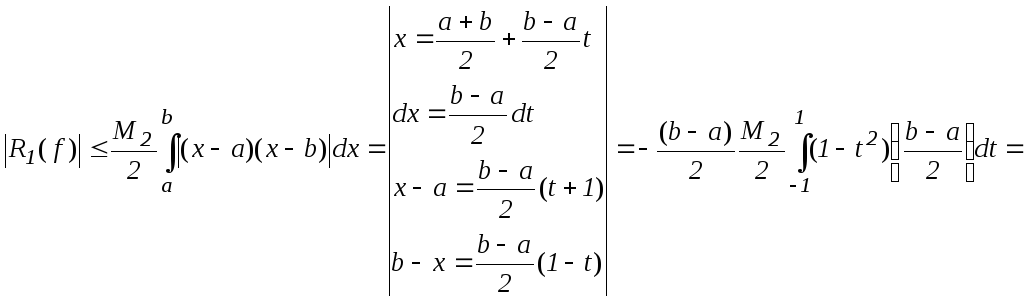
(11)

Формулы Ньютона-Котеса.

Для повышения точности формулы трапеций введем на более густую равномерную сетку с шагомh: ,,.Используя полученное разбиение, запишеми применим на каждом отрезкеформулу трапеций (10), (12) где, согласно (11).

Формула (12) носит название обобщенной формулы трапеций

Определение.Квадратурные формулы с равноотстоящими узлами носят название формул Ньютона-Котеса порядка n с (N+1) узлами, где n- порядок интерполяции.

(12) – формула Ньютона-Котеса порядка n=1 c (N+1) узлами.

Определение.Говорят, что данная квадратурная формула имеет алгебраическую точность , еслидля многочлена степени меньшей или равнойформула трапеций (10)-точна для многочлена, то есть, имеет алгебраическую точность 1.

18 Квадратурные формулы Гаусса-Кристоффеля.

Рассмотрим общую задачу численного интегрирования с весовой функцией . При построении квадратурных формул интерполяционного типа необходимо ввести дополнительно условие на весовую функцию:(1) Запишем квадратурную формулу для произвольного, но фиксированного распределения узлов:

. (2)

При построении квадратурных формул Ньютона-Котеса узлы распределялись равномерно по отрезку [a,b]. Очевидно, что такой способ выбора узлов становится невозможным для несобственных интегралов с бесконечными пределами.

Возникает вопрос: как выбрать систему узлов квадратурной формулы, чтобы формула (2) имела наивысшую возможную алгебраическую степень точности?

Напомним, что квадратурная формула имеет алгебраическую степень точности , если она точна для многочленов степени меньшей или равной.

Заметим, что формула (2) содержит всего 2n неизвестных параметров (n узлов и n весовых коэффициентов). Столько же коэффициентов содержит и произвольный многочлен степени 2n-1.

Таким образом, наивысшая алгебраическая степень точности формулы (2) не может быть больше 2n-1.