10. Классические ортогональные многочлены и их применение в задачах приближения функций.

Пусть H- гильбертово пространство со скалярным произведением <f,g> и, соответственно, нормой . Важным примером такого пространства является так называемое пространство- пространство функцийf(x), для которых конечен интеграл:

(1)

Здесь h(x)- так называемая весовая функция, удовлетворяющая условиям:1.h(x)0 на [a,b].

2.Если промежуток [a,b]- конечный, то существует и конечен;Если же [a,b]=(0,+), то должно выполняться условие:т.е. должны существовать любые моменты весовой функции.

Определение 1.Для определено скалярное произведение:

(2)

и соответственно норма:согласно условию (1).

Используя неравенство Коши – Буняковского - Шварца, получаем

Поэтому скалярное произведение существует для

Определение 2.Расстояние между элементами f и g определяется равенством:.

Возникает вопрос о том, как понимать нулевой элемент. Если норма , следует ли отсюда, чтоf=g? Вводится терминология:f=gпочти всюду, то есть они могут отличаться в конечном числе точек.

Определение 3.f и g ортогональны на отрезке [a,b] с весом h(x), если <f,g>=0 (кратко пишут ).Если в гильбертовом пространстве взять любую линейно независимую систему,i=0,1,2,…, то ее можно ортогонализировать.

Рассмотрим в качестве примера систему: Приконечный набор степенных функций линейно независим, поэтому на базе этой системы можно построить ортогональные полиномы. Известна следующая рекуррентная процедура ортогонализации (процедура Грама - Шмидта):(3)

Коэффициенты b_k+1,j определяются из условий ортогональности:Последовательно умножая (3) на получаем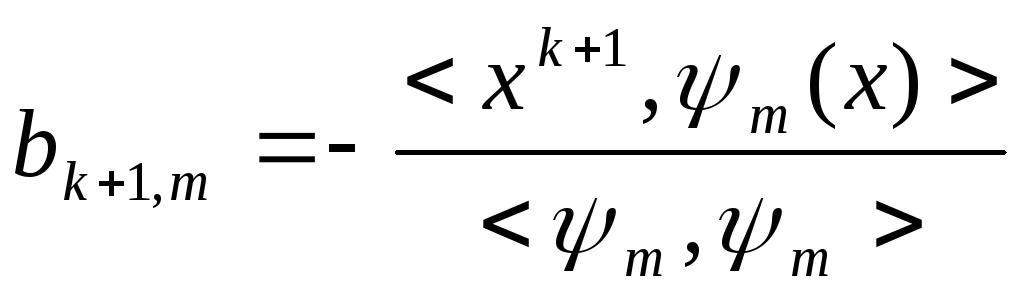(4)

11.Полиномы Лежандра. Построение и использование в задачах ср.Кв.Приближения.

Пусть h(x)1, [a,b]=[-1,1].Построить первые три ортогональных полинома по процедуре (3) - (4).(см 10)

Далее имеем:

,

следовательно,Действуя, аналогично далее, получаем:

Для системы ортогональных многочленов на отрезке [-1,1] с весом h(x)=1 справедлива формула Родрига: (5)

Из (5) последовательно получаем:

и т.д. Получаемые таким образом полиномы называются полиномами Лежандра.

Замечание. Найденные по процедуре (3) – (4) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по явной формуле Родрига (5).

Квадрат нормы у этих полиномов равен: То есть эти многочлены не нормированы, так какДля всех классических многочленов существует рекуррентная формула. Для полиномов Лежандра она имеет следующий вид:

(6)

Пусть Рассмотрим среднеквадратичное приближение:

где - среднеквадратичная ошибка аппроксимации,- отрезок ряда Фурье для функцииf(x) по системе ортогональных многочленов {P_k(x)}.В силу ортогональности многочленов Лежандра, система нормальных уравнений (2) из §1.5 становится диагональной, и ее решение приводит к следующим выражениям для коэффициентов c_k:

(7)

При этом то есть обеспечивается минимум нормы вL₂.

Распишем подробно ошибку аппроксимации

(8)

С другой стороны

в силу ортогональности.

Подставляя в (8), получим

. (9)

Пример 2.

Пусть f(x)=|x|.

Аппроксимировать f(x) на [-1,1] в среднеквадратичном многочленом второй степени. Вычислить среднеквадратичную ошибку.

Используем ортогональную систему Лежандра:

Коэффициенты c_k находим по формуле (7), учитывая вид полиномов Лежандра:

Далее вычисляем среднеквадратичную ошибку по формуле (9):