
- •1. Структура погрешности в численном анализе.
- •2.3.Округление.
- •4. Понятие близости в метрическом пространстве.
- •Примеры классов функций и соответствующих нормированных пространств.
- •Задача наилучшего приближения в нормированном пространстве.
- •Задача приближения полиномами.
- •Интерполяция.
- •Конечные разности.
- •7.Интерполяционный многочлен Ньютона.
- •6.Запись интерполяционного многочлена для равноотстоящих узлов.
- •9. Среднеквадратичное приближение функции.
- •10. Классические ортогональные многочлены и их применение в задачах приближения функций.
- •11.Полиномы Лежандра. Построение и использование в задачах ср.Кв.Приближения.
- •С другой стороны
- •12. Некоторые общие свойства ортогональных полиномов.
- •13. Многочлены Чебышева, их свойства .
- •14.Первые применения многочленов Чебышева к задаче интерполяции.
- •15. Квадратурные формулы на основе интерполяций.
- •Формулы Ньютона-Котеса.
- •18 Квадратурные формулы Гаусса-Кристоффеля.
- •19. Запишем квадратурную формулу для произвольного, но фиксированного распределения узлов :
- •21 .Принцип сжатых отображений.
- •23 Метод Ньютона.
- •24.Численные методы линейной алгебры.
- •27 Стационарные итерационные процедуры. Теоремы о сходимости.
- •33-34Численное дифференцирование.
- •35-36.Численные методы решения задачи Коши.
- •37-39.Методы Рунге-Кутта.
- •41.Постановка краевой задачи для оду второго порядка:
- •47.Аппроксимация, устойчивость и сходимость разностных схем.
1. Структура погрешности в численном анализе.
Основные источники погрешностей:
Погрешности математической модели.Любая задача есть модель какого-то явления. Всякая модель – это объект более простой, чем реальный. Модель – приближенное описание реального объекта, т.е. содержит погрешности.
Погрешности исходных данных.Данные могут оказаться неточными.
Погрешности метода решения.исленные методы заменяют задачу на близкую. Например, вместо интегрирования – суммирование, вместо дифференцирования – вычисление конечно разностного отношения и т.д. В результате вместо точного решения исходной задачи получаем приближенное решение преобразованной задачи.
Погрешности округлений при выполнении арифметических операций.
В рамках численных методов погрешности 1 и 2 считаются неустранимыми.
Рассмотрим подробнее пункт 4.
Пусть
![]() - приближенное представление числаX,
т.е.
- приближенное представление числаX,
т.е.![]() ,
,
где
![]() - погрешность.
- погрешность.
Определение
1.Величина
![]() называетсяабсолютной
погрешностью
представления числа X
с помощью числа
называетсяабсолютной
погрешностью
представления числа X
с помощью числа
![]() .Максимально
возможное значение
.Максимально
возможное значение![]() ,
т.е. число
,
т.е. число![]() ,
удовлетворяющее неравенству
,
удовлетворяющее неравенству![]() ,
называетсямаксимальной,
или предельной,
абсолютной
погрешностью
(ошибкой).
,
называетсямаксимальной,
или предельной,
абсолютной
погрешностью
(ошибкой).
Определение
2.Величина,
равная
![]() ,
называетсяотносительной
ошибкой
представления числа X
числом
,
называетсяотносительной
ошибкой
представления числа X
числом
![]() .Если
.Если![]() ,
то число
,
то число![]() называетсямаксимальной
предельной относительной ошибкой.
называетсямаксимальной
предельной относительной ошибкой.
2.3.Округление.
Обычно при вычислении
с плавающей запятой число X
представляется в нормализованном
виде.![]() ,гдеf
- мантисса числа X,
,гдеf
- мантисса числа X,
![]() ,
,
а
- основание системы счисления (а=2,8,10
и т.д.), L
– порядок числа,
![]() .
.
Кроме того,![]() ,
,![]() - цифра в k-ом разряде дробного числа,
- цифра в k-ом разряде дробного числа,![]() .
.
t – порядок числа - число используемых значащих цифр (характеристика вычислительного устройства).
Определение 3.Пусть число X записано в позиционной системе счисления. Значащими называются все цифры, начиная от первой слева не равной 0.Если число значащих цифр в представлении X превосходит t, то происходит округление.Ошибки округления распространяются дальше при выполнении арифметических операций.
Рассмотрим некоторые примеры.
Пример 1.Абсолютная погрешность суммы.
Пусть
![]() ,
,![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() .
.
Т.к.
![]() ,
то
,
то![]() ,
т.е. предельные абсолютные ошибки
складываются.
,
т.е. предельные абсолютные ошибки
складываются.
Пример 2.То же самое для разности. Предельные максимальные абсолютные погрешности аналогично складываются.
Пример 3.Относительные погрешности произведения.
![]() ,
где
,
где
![]() ,
,
![]() ,
где
,
где
![]() .
.
Считаем, что последнее слагаемое имеет второй порядок малости по сравнению с первыми двумя, и им пренебрегаем.
![]() ,
,
![]() ,
,
тогда
получаем![]() ,
т.е.
,
т.е.![]() .
.
При умножении относительные максимальные ошибки приближенно складываются.
Пример 4.Деление.
При делении относительные максимальные ошибки также складываются.
4. Понятие близости в метрическом пространстве.
Определение
1.Множество
X
элементов произвольной природы (не
обязательно числовое множество)
называется метрическим
пространством,
если любой паре элементов
![]() поставлено в соответствие число
поставлено в соответствие число![]() ,
(метрика, или расстояние) в соответствии
с аксиомами:А1.
,
(метрика, или расстояние) в соответствии
с аксиомами:А1.![]() тогда и только тогда, когдаx=y.А2.
тогда и только тогда, когдаx=y.А2.
![]() .
.
А3.
![]() – неравенство треугольника.
– неравенство треугольника.
Определение
2.Говорят,
что последовательность элементов
![]() метрического пространстваX
сходится к элементу
метрического пространстваX
сходится к элементу
![]() ,
если
,
если![]() .
.
Определение
3.Последовательность
![]() элементов метрического пространстваX
называется фундаментальной,
если
элементов метрического пространстваX
называется фундаментальной,
если
![]() .
.
Определение
4.Метрическое
пространство X
называется полным,
если любая фундаментальная последовательность
![]() его элементов сходится к некоторому
элементу этого пространства. Замечания.1Не
любое метрическое пространство является
полным.
его элементов сходится к некоторому
элементу этого пространства. Замечания.1Не
любое метрическое пространство является
полным.
Например, множество
всех рациональных чисел с метрикой
![]() не является полным, т.к., скажем,
последовательность
не является полным, т.к., скажем,
последовательность![]() - фундаментальная, но
- фундаментальная, но![]() - иррациональное число.2 Сходимость
большинства итерационных процессов
удается доказать только в полном
метрическом пространстве, следовательно,
полнота играет важную роль в числовом
анализе.
- иррациональное число.2 Сходимость
большинства итерационных процессов
удается доказать только в полном
метрическом пространстве, следовательно,
полнота играет важную роль в числовом
анализе.
Определение 5.Множество X называется нормированным линейным пространством, если
оно является линейным пространством, т.е. в нем определены операции сложения элементов и умножения элемента на число с известными свойствами.
любому элементу
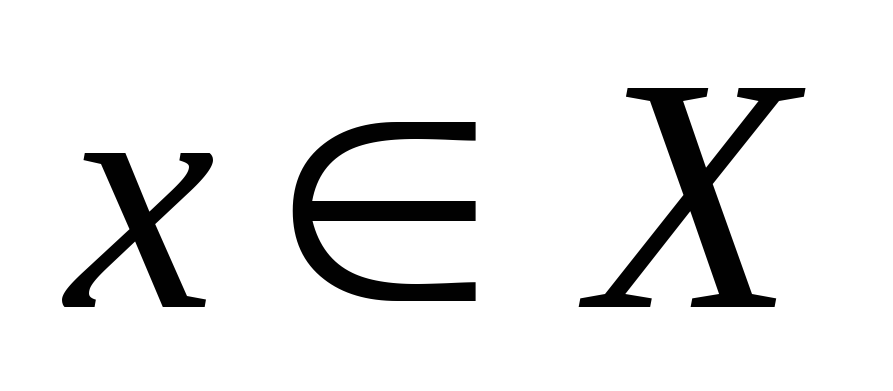 поставлено в соответствие число
поставлено в соответствие число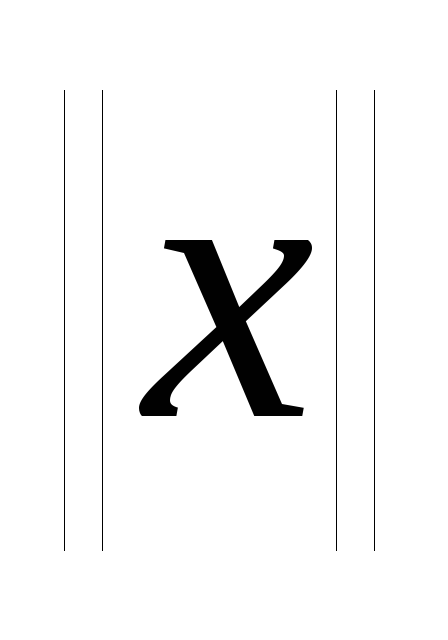 (нормаx),
удовлетворяющее аксиомам:А1.
(нормаx),
удовлетворяющее аксиомам:А1.
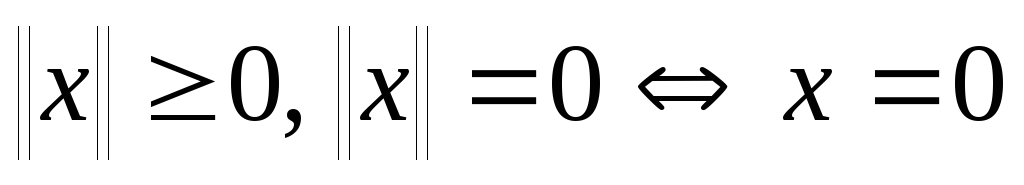 ,А2.
,А2.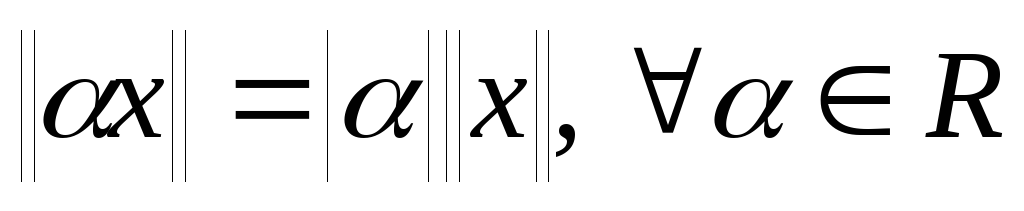
А3.
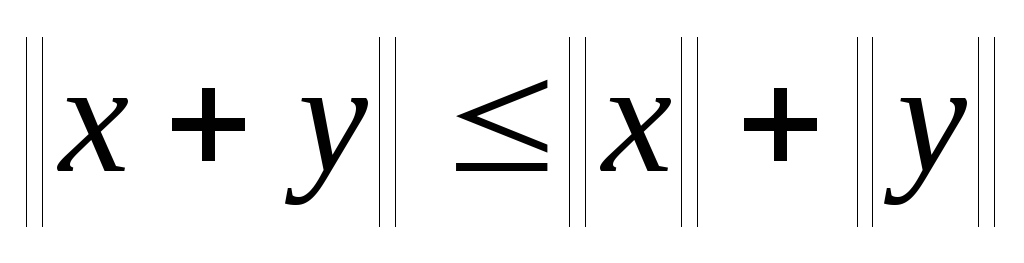 –
неравенство треугольника.
–
неравенство треугольника.
Замечание.Любое
нормированное линейное пространство
X
можно считать метрическим, введя метрику
по формуле![]() . (1)
. (1)
Если последовательность
![]() нормированного пространстваX
сходится в смысле метрики (1), то говорят
о сходимости по норме пространства X.
нормированного пространстваX
сходится в смысле метрики (1), то говорят
о сходимости по норме пространства X.
Нетрудно убедиться, что для метрики (1) выполняются все аксиомы метрики.
Приведем некоторые примеры классов функций и соответствующих линейных пространств.
