Применим окно Ханна для синтеза дискретного ФНЧ 32
порядка. S( f ) Hann window
0 |
|
|
|
|
|
20 |
|
|
|
|
|
40 |
|
|
|
|
|
60 |
|
|
|
|
|
80 |
|
|
|
|
|
1000 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
f/F |
|
|
Здесь результат получился лучше, чем для треугольного окна и |
|||||
окна Бартлетта, так уровень первого бокового лепестка в полосе |
|||||
задерживания равен –44 дБ. |
|
|
61 |
||
Окно Хэмминга
Отсчеты окна Хэмминга рассчитываются по формуле
w(k) 0.54 |
|
k 1 |
|
, 1 k n |
|
|
0.46 cos 2 |
|
|
|
(55) |
||
|
|
n 1 |
|
|
||
|
|
|
|
|
||
На рисунках показаны весовая функция окна Хэмминга, и ее спектр.
62
w( n ) Hamming
0.15 |
|
|
|
|
0.1 |
|
|
|
|
0.05 |
|
|
|
|
00 |
5 |
10 |
15 |
20 |
63
S( f ) Hamming
0 |
|
|
|
|
20 |
|
|
|
|
40 |
|
|
|
|
60 |
|
|
|
|
800 |
2 |
4 |
6 |
8 |
|
|
f/F |
|
|
|
Уровень бокового лепестка составляет –40 дБ. |
64 |
||
|
|
|
|
|
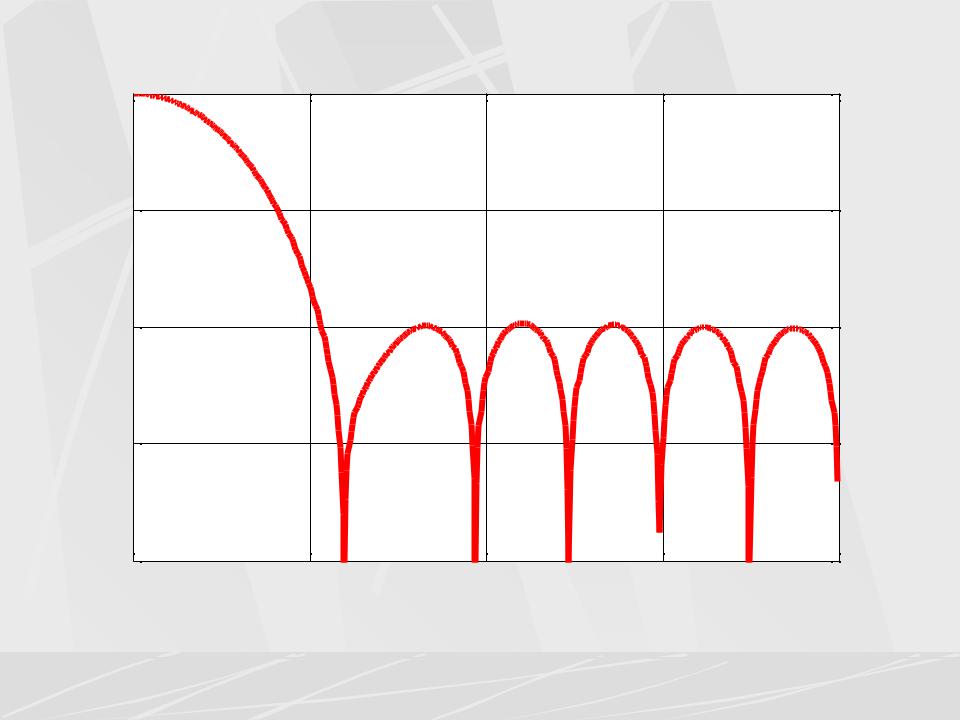
Применим окно Хэмминга для синтеза дискретного ФНЧ 32
порядка. |
S( f ) Hamming window |
|
0 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
40 |
|
|
|
|
|
|
60 |
|
|
|
|
|
|
800 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
|
f/F |
|
|
|
Окно Хэмминга дает еще лучший результат, так уровень первого |
||||||
бокового лепестка в полосе задерживания равен –53.6 дБ. |
65 |
|||||
Окно Блэкмена
Отсчеты окна Блэкмена рассчитываются по формуле .
w(k) 0.42 |
|
2 |
|
k 1 |
|
|
4 |
k 1 |
, |
(55) |
|
0.5 cos |
|
|
0.08 cos |
|
|
||||||
|
|
|
|
n 1 |
|
|
n 1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
1 k n
На рисунках показаны весовая функция окна Блэкмена, и ее спектр.
66
w( n ) Blackman
0.15
0.1
0.05
00 |
5 |
10 |
15 |
20 |
67
S( f ) Blackman
0 |
|
|
|
|
20 |
|
|
|
|
40 |
|
|
|
|
60 |
|
|
|
|
80 |
|
|
|
|
1000 |
2 |
4 |
6 |
8 |
|
|
f/F |
|
|
|
Уровень бокового лепестка составляет –58 дБ. |
68 |
||
|
|
|
|
|
Применим окно Блэкмена для синтеза дискретного ФНЧ 32 |
|||||
порядка. |
|
S( f ) Blackman window |
|
|
|
0 |
|
|
|
|
|
20 |
|
|
|
|
|
40 |
|
|
|
|
|
60 |
|
|
|
|
|
80 |
|
|
|
|
|
1000 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
f/F |
|
|
Окно Блэкмена дает лучший результат чем окно Хэмминга, так |
|||||
уровень первого бокового лепестка в полосе задерживания |
|||||
равен –75.3 дБ. Правда окно Хэмминга дает более узкую |
|||||
переходную полосу между полосой пропускания и полосой |
|||||
задерживания. |
|
|
|
|
69 |
Окно Кайзера
Отсчеты окна Кайзера рассчитываются по формуле :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 |
|
1 |
|
2k n 1 |
|
2 |
(56) |
||||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
w(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
1 k n |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
I0 ( ) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь I0 (z) - модифицированная функция Бесселя первого рода
нулевого порядка. Параметр может меняться от 0 до , но на практике используются значения от 4 до 9.
На рисунках показаны весовая функция окна Кайзера, и ее спектр для =9 .
70