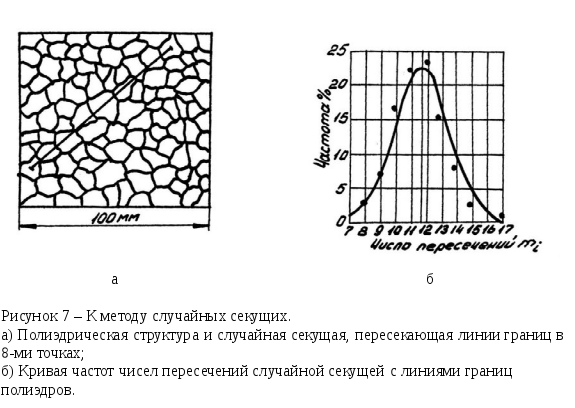
Пример:

Пусть имеется микрофотография травленного шлифа (увеличение 440). Проведём на ней 8 секущих отрезков: 4 по 70 миллиметров и 4 по 80 миллиметров. Получим соответствующее число пересечений каждой секущей с границами зёрен: 1-я – 17, 2-я – 22, 3-я – 20, 4-я – 21, 5-я – 20, 6-я – 22, 7-я – 25, 8-я – 23 пересечений. Тогда в соответствии с вышеописанной методикой средний размер зерна будет равен:

Ответ получился в микрометрах, так как длины секущих подставлялись в мм, а перед скобкой имелся множитель .

Метод Джеффриса-Салтыкова

По этому методу можно осуществлять первоначальную статистическую обработку микрофотографий. Метод заключается в следующем: подсчёт количества плоских зёрен производится на площади квадрата или прямоугольника. При этом предполагается, что линии, ограничивающие выбранный участок (), рассекают зерна на две в среднем равные половины. Между тем, прямые углы вершин квадрата или прямоугольника, попадая на площадь зерна, отсекают от него в среднем лишь одну четвёртую часть площади. Таким образом, расчёт приведённого количества зёрен проводится по формуле:

где z– количество целых зёрен внутри прямоугольника или квадрата;w– количество зёрен, пересечённых прямыми линиями контура, за вычетом 4-х угловых зёрен.

Число зёрен на 1 шлифа:

Средний размер зерна рассчитывают, исходя из выбора плоских сечений зёрен для 200-250 частиц, по формуле:

,

где - сумма средних значений плоских зёрен в мм;

z– количество целых зёрен внутри прямоугольника или квадрата;

1000 – коэффициент пересчёта в мкм;

N– увеличение.

Для керамической структуры наиболее целесообразно использовать значение среднего размера кристаллитов и дисперсию распределения частиц по размерам.

В спечённом материале распределение кристаллитов по размерам в большинстве случаев подчиняются нормальному закону:

,

где - математическое ожидание случайной величиныx;- среднеквадратичное отклонение.

Экспериментально установлено, что случайной величиной, подчиняющейся нормальному закону распределения, чаще всего является , а на начальной стадии спекания -. В последнем случае можно написать:

,

где - число частиц с размером;

- общее число частиц.

Следовательно, кривая накопления может быть представлена уравнением:

,

где - число частиц с;

.

Правая часть уравнения представляет собой интеграл вероятности, значения которого табулированы. Воспользовавшись соответствующими таблицами, по известным из экспериментальных данных величинам легко определить значения. Таким образом, при выполнении нормального закона распределения зависимость междуUиDлинейная. Тангенс угла наклона этой прямой равен, апри. Последнее реализуется при.

Когда линейная зависимость между переменными UиDотсутствует (т.е. кривыеимеют явно выраженную асимметрию), рассчитывают коэффициент ассиметрии А и эксцесса Е, количественно характеризующие степень отклонения от нормального закона распределения.

Таким образом, наиболее однородная керамическая структура характеризуется минимальным значением дисперсии распределения кристаллитов по размерам и условием .