Кодирование информации

УДК 681.3 (076)

ББК 32.811.4 я7 К 57

Одобрено секцией методических пособий научно-методического совета университета

Рецензент канд. техн. наук, доцент кафедры ТОР УлГТУ Б. Н. Романов

Изложены основные положения теории и методики построения эффективных кодов, оптимальных с точки зрения минимальной средней длины кодовых слов: код Шеннона-Фэно, Хаффмена, префиксные коды. Особое внимание уделено теории помехоустойчивого кодирования, построению корректирующих кодов. Рассмотрены способы обнаружения и исправления ошибок в групповых, циклических кодах, в коде Хемминга.

В ходе изложения теоретического материала рассмотрен ряд задач, что в значительной степени упрощает процесс усвоения. После каждого раздела даны задания.

Приведенный материал может быть использован при подготовке к практическим занятиям по курсу «Прикладная теория информации» студентами, обучающимися по специальностям 23020165 «Информационные системы и технологии» и 200103165 «Авиационные приборы и измерительновычислительные комплексы».

Методические указания подготовлены на кафедре ИВК.

УДК 681.3 (076) ББК 32.811.4 я7

© В. Д. Горбоконенко, В. Е. Шикина, составление, 2006 © Оформление. УлГТУ, 2006

Учебное издание

КОДИРОВАНИЕ ИНФОРМАЦИИ

Методические указания

Составители: ГОРБОКОНЕНКО Вера Дмитриевна ШИКИНА Виктория Евгеньевна

Редактор Н. А. Евдокимова

Подписано в печать 30.03.2006. Формат 60×84/16. Бумага офсетная. Печать трафаретная. Усл. печ. л. 3,03. Уч.-изд. л. 3,00. Тираж 100 экз.

Заказ .

Ульяновский государственный технический университет 432027, г. Ульяновск, ул. Сев. Венец, д. 32.

Типография УлГТУ, 432027, г. Ульяновск, ул. Сев. Венец, д. 32.

СОДЕРЖАНИЕ

55

РАЗДЕЛ 1. ЭФФЕКТИВНОЕ КОДИРОВАНИЕ

1.1. Общая характеристика эффективного кодирования

Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволяет уменьшить время передачи или объем запоминающего устройства.

Такое эффективное кодирование базируется на основной теореме Шеннона для каналов без шума.

Шеннон доказал, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.

1.2. Методика Шеннона – Фэно

При отсутствии статистической взаимосвязи между буквами конструктивные методы построения эффективных кодов были даны впервые Шенноном и Фэно. Их методики существенно не различаются, поэтому соответствующий код получил название кода Шеннона – Фэно.

Код строится следующим образом: буквы алфавита сообщений выписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей в каждой из групп были по возможности одинаковы. Всем буквам верхней половины в качестве первого символа приписывается 1, а всем нижним 0. Каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и т. д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Рассмотрим алфавит из восьми букв. Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется три символа.

Наибольший эффект сжатия получается в случае, когда вероятности букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии. Убедимся в этом, вычислив энтропию

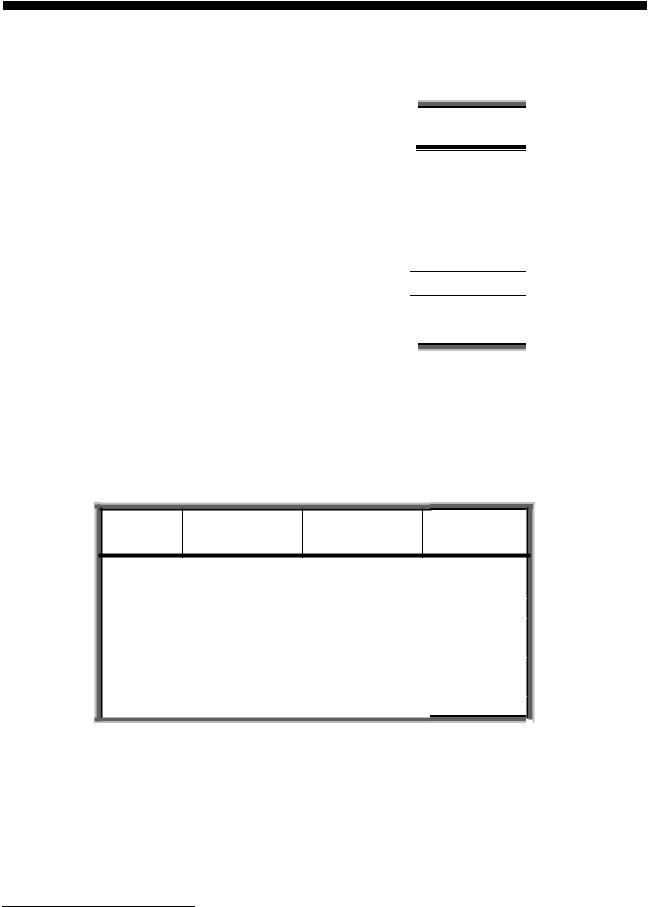
где n(zi) – число символов в кодовой комбинации1, соответствующей букве zi. Характеристики такого ансамбля и коды букв представлены в табл.1.1.

В более общем случае для алфавита из восьми букв среднее число символов на букву будет меньше трех, но больше энтропии алфавита H(z).

Для ансамбля букв, приведенного в табл. 1.2, энтропия равна 2,76, а среднее число символов на букву 2,84.

Табл. 1.2

Буквы Вероятности Кодовые Ступень комбинации разбиения

Следовательно, некоторая избыточность в последовательностях символов осталась. Из теоремы Шеннона следует, что эту избыточность также можно устранить, если перейти к кодированию достаточно большими блоками.

1 Число разрядов в кодовой комбинации здесь и в дальнейшем обозначено через п для того, чтобы избежать расхождения с общепринятой терминологией в области эффективного и помехоустойчивого кодирования.

4

1.3. Кодирование блоками

Рассмотрим сообщения, образованные с помощью алфавита, состоящего всего из двух букв z1 и z2 с вероятностями появления соответственно p(z1)=0,9 и p(z2)=0,1.

Поскольку вероятности не равны, то последовательность из таких букв будет обладать избыточностью. Однако при побуквенном кодировании никакого эффекта не получается.

Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна 0,47.

При кодировании блоков, содержащих по две буквы, получим коды, показанные в табл. 1.3.

Так как буквы статистически не связаны, вероятности блоков определяются как произведение вероятностей составляющих букв.

Среднее число символов на блок получается равным 1,29, а на букву

0,645.

Кодирование блоков, содержащих по три буквы, дает еще больший эффект. Соответствующий ансамбль и коды приведены в табл. 1.4.

5

Среднее число символов на блок равно 1,59, а на букву 0,53, что всего на 12% больше энтропии. Теоретический минимум Н(z)=0,47 может быть достигнут при кодировании блоков, включающих бесконечное число букв:

Следует подчеркнуть, что увеличение эффективности кодирования при укрупнении блоков не связано с учетом все более далеких статистических связей, так как нами рассматривались алфавиты с некоррелированными буквами. Повышение эффективности определяется лишь тем, что набор вероятностей, получающийся при укрупнении блоков, можно делить на более близкие по суммарным вероятностям подгруппы.

1.4. Методика Хаффмена

Рассмотренная нами методика Шеннона – Фэно не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу. Множество вероятностей, приведенных в табл. 1.2, можно было бы разбить иначе, например, так, как это показано в табл. 1.5.

При этом среднее число символов на букву оказывается равным 2,80. Таким образом, построенный код может оказаться не самым лучшим. При построении эффективных кодов с основанием m>2 неопределенность становится еще больше.

От указанного недостатка свободна методика Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Для двоичного кода методика сводится к следующему. Буквы алфавита сообщений выписываются в основной столбец в порядке убывания вероятностей. Две последние буквы объединяются в одну вспомогательную

6

букву, которой приписывается суммарная вероятность. Вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Методика поясняется примером, представленным табл. 1.6. Значения вероятностей приняты те же, что и в ансамбле табл. 1.2.

Табл. 1.6

Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода сообщения по строкам и столбцам таблицы.

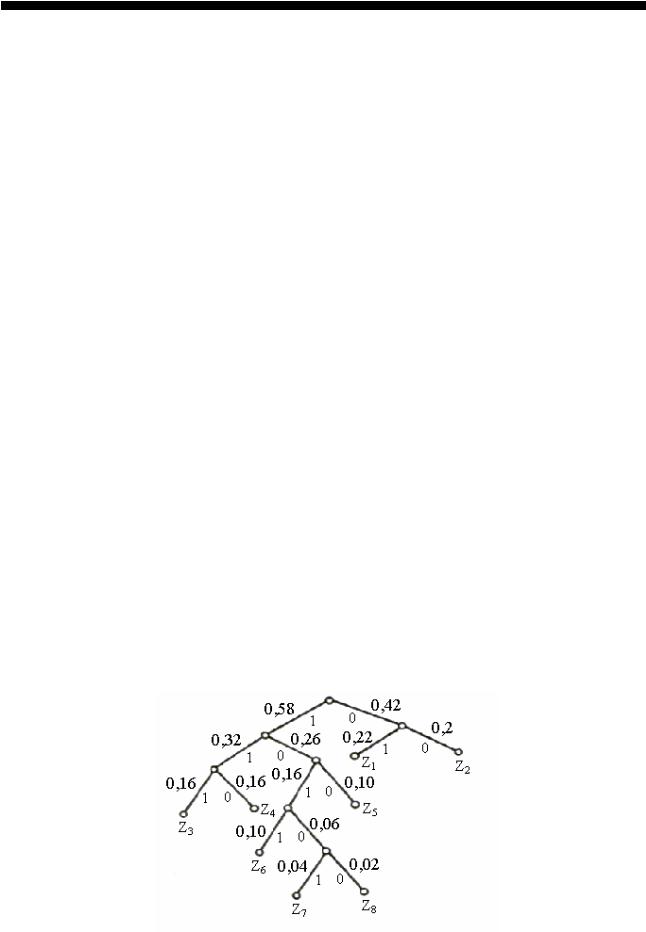
Для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваивается символ 1, а с меньшей 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждой буквы. Кодовое дерево для алфавита букв, рассматриваемого в табл. 1.6, приведено на рис. 1.1.

Рис. 1.1. Кодовое дерево, построенное по табл. 1.6, в соответствии с методом Хаффмена

7