1.5. Производящие функции и рекуррентные соотношения.

В результате выполнения алгебраических преобразований могут осуществляться определенные комбинаторные подсчеты. С этим мы уже встретились в 1.2 при выводе биномиальной формулы, когда комбинаторные объекты – числа сочетаний появились в новом качестве биномиальных коэффициентов при выполнении алгебраической операции возведения в степень. Рассмотрим еще примеры, иллюстрирующие эту связь между алгеброй и комбинаторикой.

Пусть в урне находятся 3 красных, 4 синих и 2 зеленых шара. Сколькими способами могут быть извлечены 6 шаров, если считать шары одного цвета между собой неразличимыми? Для ответа на этот вопрос достаточно по обычным алгебраическим правилам раскрыть скобки в выражении

,

привести подобные члены и взять коэффициент при . Здесь первая скобка соответствует красным шарам, вторая синим и третья  зеленым. При перемножении степеней буквы , взятых из различных скобок, показатели степеней складываются, поэтомувозникнет столько раз, сколько существует способов выбора 6 шаров. Это рассуждение справедливо не только для, но и для любой другой степени. Выполнив умножение, получаем многочлен

,

который называется производящей функцией для числа способов выбора, так как коэффициент при равен числу способов выборашаров. В частности, 6 шаров могут быть извлечены 9 способами.

Несколько видоизменим задачу. Пусть требуется найти число извлечений, содержащих нечетное число красных шаров, четное число синих и хотя бы один зеленый шар. В этом случае также легко выписать производящую функцию, дающую ключ к решению задачи:

.

Теперь 6 шаров могут быть извлечены лишь двумя способами.

Другой пример. Пусть требуется набрать денежную сумму 10 рублей, имея четыре монеты 1 рубль, три монеты  2 рубля, две монеты  5 рублей и одну монету  10 рублей. Сколькими способами это можно сделать?

Рассмотрим выражение

,

в котором каждая скобка соответствует одному из номиналов. Показатели степени, в которые возводится буква в скобке, равны произведению номинала монеты на число монет данного номинала, которое может быть включено в набираемую денежную сумму. Это число изменяется от нуля до количества имеющихся в распоряжении монет данного номинала. Так как при умножении показатели степени складываются, то ответ на вопрос задачи даст после перемножения скобок коэффициент при. Выполнив умножение, получим:

.

Таким образом, набрать 10 рублей можно пятью способами. Вот они:

.

Конечно, проще было бы решить задачу, просто указав 5 возможных вариантов, однако полученный в результате перемножения скобок степенной ряд позволяет для любого дать ответ на вопрос, сколькими способами может быть получена денежная сумма в количестверублей. Он является производящей функцией для числа способов набора денежных сумм.

Производящие функции берут свое начало в работах Муавра, Эйлера и Лапласа. Идея метода производящих функций состоит в том, чтобы сопоставить последовательности решений задачи функцию (степенной ряд), аналитические методы работы с которой оказываются проще и эффективнее комбинаторных методов работы с последовательностями.

Перейдем к формальным определениям. С каждой числовой последовательностью можно связать степенной рядкоторый называется производящей функцией последовательности. Если рядсходится в некоторой окрестности нуля, он является рядом Маклорена для функции. Поэтому знание производящей функции позволяет восстановить исходную последовательность:

.

Полезно знать производящие функции для простейших последовательностей.

Для последовательности, состоящей из единиц (), производящая функция

.

Это есть хорошо известная из школьного курса математики формула для суммы бесконечно убывающей геометрической прогрессии. Почленным дифференцированием из нее получаем, что производящая функция для последовательности () есть

С помощью (k-1) – кратного дифференцирования можно получить и более общую формулу, являющуюся производящей функцией для числа сочетаний с повторениями :

;

;

.

Полезно также следующее непосредственно проверяемое тождество

Теперь, вооруженные уже определенными техническими средствами, перейдем к задачам, решение которых методом производящих функций путем прямого перемножения скобок было бы достаточно утомительным.

Какова вероятность при бросании 4 игральных костей выбросить 14 очков? Эта вероятность равна отношению числа способов выбросить 14 очков к полному числу возможных выпадений 4 различных костей. Подсчет полного числа выпадений 4 различных костей не составляет труда. Так как каждая кость имеет 6 граней, то это число равно . Сложнее найти число способов, которыми может быть выброшено 14 очков. Ответом на этот вопрос является коэффициент прив выражении. Здесь каждая из четырех скобок, возникающих при записи степени в виде произведения, соответствует одной из игральных костей, а степени переменной числу возможных выпадений очков на ней. После выполнения алгебраических преобразований коэффициенты степенного ряда укажут число способов получения любой суммы от 4 до 24. Поэтому полученный степенной ряд (в данном случае конечный) называется производящей функцией для числа способов выпадения различных сумм в четырех бросаниях. Найдем эту производящую функцию.

=.

Легко видеть, что степень возникает в двух случаях: когда в первой сумме, а во второй, и когда в первой сумме, а во второй. Поэтому коэффициент приравен. Таким образом, искомая вероятность равна

.

Чтобы сравнить возможности различных подходов для решения задач перечисления, рассмотрим задачу из раздела 1.3., решенную там с помощью формулы включения и исключения, и решим её методом производящих функций.

Пусть требуется найти число целочисленных решений системы

Легко понять, что искомое число решений есть коэффициент при после раскрытия скобок в выражении

Более общё, можно сказать, что выписанное выражение является производящей функцией для числа решений системы

так как при любом целом коэффициент приравен числу решений. Найдем коэффициент при:

.

В коэффициент при дают вклад значения. Поэтому число решений равно

.

Производящие функции являются мощным средством для решения рекуррентных соотношений, т.е. определении последовательностей, последующие члены которых выражаются через предыдущие. Простейшими рекуррентными последовательностями являются арифметическая и геометрическая прогрессии, у которых каждый последующий член определяется предыдущим, а первый член задается.

Рассмотрим пример рекуррентной последовательности, у которой каждый член, начиная с третьего выражается через два предыдущих, а два первых члена заданы: ,,. С помощью рекуррентного соотношения, используя заданные значенияи, получаем,и т.д. Воспользовавшись методом производящих функций, найдем в явном виде формулу-го члена.

Домножив обе части рекуррентного соотношения на и просуммировав по, получим

.

Отсюда для производящей функции

имеем соотношение:

;

.

Разрешая его относительно , получаем

.

Воспользовавшись приведенным выше разложением для , перепишем формулу дляв виде

.

Это позволяет выписать формулу -го члена:

.

Рассмотрим теперь другой, более интересный пример, показывающий, как рекуррентные соотношения возникают в реальных перечислительных задачах. Пусть требуется найти число двоичных последовательностей длины, не содержащих двух единиц подряд. Приимеются две таких последовательности:и. Притаких последовательностей три:. Поэтому,.

Разобьем искомое множество последовательностей на 2 подмножества: последовательности, начинающиеся с 0, и последовательности, начинающиеся с 1. Последовательности первого типа не имеют каких-либо дополнительных ограничений на последующие символов. Поэтому их. Последовательности второго типа на второй позиции обязаны содержать 0, а на последующиесимволов нет каких-либо ограничений, поэтому их. Это приводит к рекуррентному соотношению

,

т.е. каждый член последовательности, начиная с третьего, равен сумме двух предыдущих членов. Положим . Тогда рекуррентное соотношение будет выполняться, начиная со второго члена. Вместе с начальными даннымиионо позволяет найти любой член последовательности. Вот перые семь членов: 1, 2, 3, 5, 8, 13, 21, … . Данная последовательность называется последовательностью Фибоначчи, по имени впервые её рассмотревшего итальянского математика 13 века. Она возникла в придуманной им своеобразной задаче о размножении кроликов.

Для получения формулы -го члена в явном виде домножим обе части рекуррентного соотношения наи просуммируем поот 2 до ∞:

.

Это позволяет для производящей функции

получить соотношение

.

Разрешая это соотношение относительно , получаем

.

Разлагаем данное рациональное выражение на простейшие дроби:

, где ,;

;

.

Подставляя , получаем

.

Подставляя , получаем

;

.

Отсюда находим

.

Несмотря на простоту исходного рекуррентного соотношения, формула общего члена оказалась не слишком простой. Во времена Фибоначчи в математике еще не было средств для её нахождения. Она была найдена значительно позже. Сам же Леонардо из Пизы наслаждался последовательным вычислением ежемесячного числа пар кроликов с помощью своего рекуррентного соотношения.

Заметим, что второй член в квадратных скобках с ростом стремится к нулю. Поэтому для нахождения-го члена последовательности достаточно найти вклад, даваемый первым членом в квадратных скобках, и округлить результат до ближайшего целого числа. Последовательность Фибоначчи обладает многими интересными свойствами и интенсивно изучалась математиками.

Завершая знакомство с производящими функциями, приведем еще два их важных свойства с примерами применения. Пусть  последовательность,  её производящая функция. Рассмотрим последовательность частичных сумм , где, с производящей функцией. Найдем связь между производящими функциямии. Для последовательностиимеет место очевидное рекуррентное соотношение:. Домножив обе его части наи просуммировав поотдо, получаем

;

.

Отсюда находим связь между производящими функциями:

.

Воспользовавшись полученным соотношением, найдем формулу для суммы квадратов первых натуральных чисел. Хорошо известно, что

.

Доказательство этой формулы является классическим примером применения метода математичкской индукции. Однако сама формула при этом должна быть как-то угадана. Метод производящих функций позволяет легко получить эту формулу и не требует никаких угадываний.

Пусть  производящая функция последовательности квадратов натуральных чисел:

.

Следовательно, производящая функция последовательности частичных сумм равна

.

Это дает искомую формулу:

.

Пусть теперь идве последовательности. Последовательностьназывается их сверткой. Перемножая производящие функциии, получаем

,

т.е. производящая функция свертки последовательностей является произведением их производящих функций.

Воспользовавшись полученным соотношением, решим задачу Эйлера о разбиении выпуклого многоугольника на треугольники диагоналями, не пересекающимися внутри многоугольника. Сколько существует подобных триангуляций? Обозначив число триангуляций -угольника через, имеем:,,,,. На рисунке представлены все 5 возможных триангуляций пятиугольника:

Найдем рекуррентное соотношение для . Пусть при некоторой триангуляции в один треугольник с вершинамиипопадает вершина. Найдем число таких триангуляций. Еслиили, то число триангуляций равно. Длячисло триангуляций равно произведению числа триангуляций-угольника на число триангуляций-угольника, т.е. равно. Таким образом, полагая, получаем длярекуррентное соотношение:

.

В правой части формулы стоит -ый член свертки последовательностис самой собою. Домножив обе части соотношения наи просуммировав поотдо, получим

.

Это дает для производящей функции соотношение

;

.

Решением квадратного уравнения, удовлетворяющим условию , является

.

Разложим в ряд. Имеем

.

Следовательно

.

Отсюда получаем

.

Числа возникают во многих задачах дискретной математики и поэтому имеют специальное название. Они называются числами Каталана по имени бельгийского математикаXIX века.

В качестве примера рассмотрим множество векторов длины , компонентами которых являютсяи, причем числоравно числу. Таких-векторов, очевидно,. Поставим теперь задачу найти среди них число тех векторов, у которых сумма любого числа первых компонент неотрицательна.

При имеем единственый такой вектор:. Притаких векторов два:и. Приподобных векторов 5:,,,и. Это есть начальные члены последовательности чисел Каталана. Покажем, что для любогочисло таких векторов равно.

Обозначим число векторов через и положим. Первая координата такого вектора всегда равна, а последняя . Поэтому число векторов, у которых для любого,, сумма первыхкоординат строго больше нуля, равно. Это число может быть записано как. Пусть для некоторого,, сумма первыхкоординат вектора первый раз обращается в нуль. Число таких векторов равно. Это позволяет записать рекуррентное соотношение

,

которое совпадает с рекуррентным соотношением для чисел Каталана. Отсюда следует, что

.

Вопросы для самопроверки.

1. Найти производящую функцию для числа способов выбрасывания 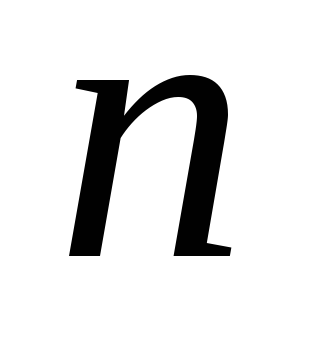очков при одновременном бросанииигральных костей.

а) ; б); в).

2. Найти производящую функцию последовательности .

а) ; б); в).

3. Сколькими способами можно расставить в очередь 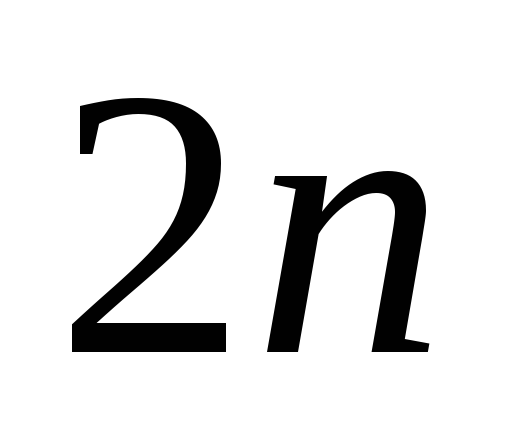человек,мужчин иженщин так, в любом начальном отрезке очереди число мужчин не превышало числа женщин? а); б); в)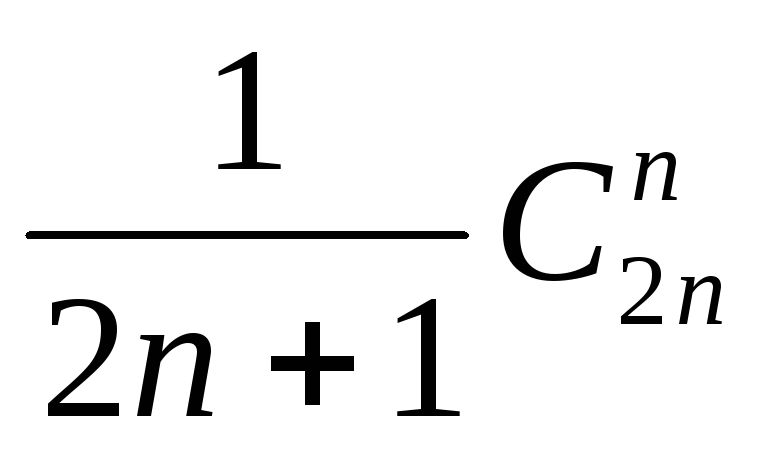.