3. Формула включения и исключения.

Чтобы найти мощность объединения двух непересекающихся множеств

нужно просто сложить их мощности: .

Если множества пересекаются,

то при сложении их мощностей каждый элемент пересечения будет посчитан дважды. Поэтому для правильного ответа необходимо из суммы мощностей вычесть мощность их пересечения: .При этом каждый элемент объединения будет посчитан ровно один раз.

Пусть теперь имеется три множества:

Теперь при сложении мощностей всех трех множеств каждый элемент, входящий ровно в два множества, будет посчитан дважды, а каждый элемент, входящий во все три множества, – трижды. Если из суммы мощностей вычесть мощности попарных пересечений, то по одному разу будут посчитаны элементы, входящие ровно в одно множество и ровно в два множества, но элементы, входящие во все три множества, не будут посчитаны ни разу. Поэтому для получения правильного ответа необходимо еще прибавить мощность пересечения всех трех множеств:

Аналогичная формула справедлива и в общем случае:

Докажем эту формулу, называемую формулой включения и исключения. Пусть элемент входит ровно вподмножеств. Вклад, который дает этот элемент в правую часть, равен

,

как это следует из тождества 4 для биномиальных коэффициентов (п. 1.2.). Поэтому вклад каждого элемента в правую часть будет равен единице, т.е. правая часть будет равна полному числу элементов, что и доказывает формулу.

В практических задачах часто имеется некоторое множество U и система его подмножеств U₁,…,U_m. Требуется найти число элементов множества U, не принадлежащих ни одному из множеств U₁,…,U_m . В этом случае формула включения и исключения выглядит следующим образом

.

Рассмотрим пример. В группе, состоящей из 20 человек, 6 знают немецкий, 7 – французский и 8 – английский язык, 3 человека знают немецкий и французский, 4 – немецкий и английский, 5 – французский и английский и один человек знает все 3 языка. Сколько человек не знают ни одного иностранного языка?

Решение: 20-(6+7+8)+(3+4+5)-1=10.

Другой пример. Пусть требуется найти число натуральных чисел, не превосходящих 100 и не делящихся ни на одно из чисел 3, 5, 7. Число чисел, делящихся на 3, равно [100/3]=33; на 5 – [100/5]=20; на 7 – [100/7]=14. Число чисел, делящихся на 3 и 5, равно [100/15]=6; на 3 и 7 – [100/21]=4, на 5 и 7 – [100/35]=2. Число чисел, делящихся на все три числа 3, 5 и 7, равно [100/105]=0. Поэтому искомое число равно 100­­–(33+20+14)+(6+4+2)–0=45.

Рассмотрим теперь пример посложнее. Пусть требуется найти число целочисленных решений системы

Формула включения и исключения оказывается полезной и здесь. Введем новые переменные ,,. Система перепишется в виде

Пусть U – множество решений системы

U₁ – множество решений системы

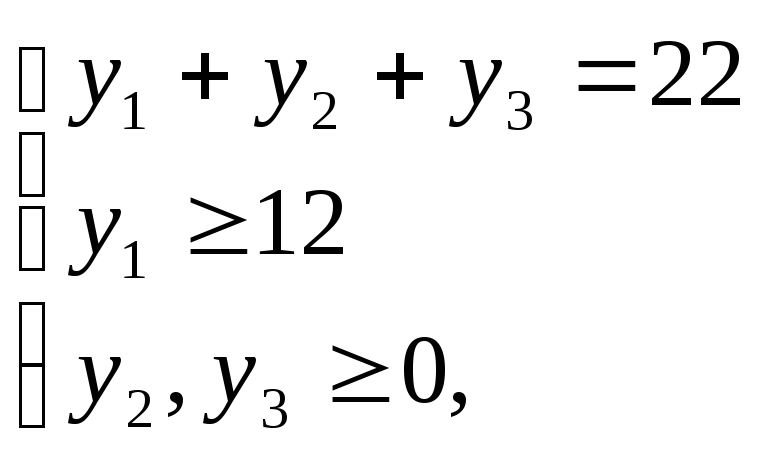
U₂ – множество решений системы

U₃ – множество решений системы

согласно п. 1.1.

Чтобы найти мощность множества U₁, достаточно в соответствующей системе сделать замену . Это дает

.

Аналогично, ,.

Далее, легко видеть, что

, ,.

Поэтому в соответствии с формулой включения и исключения число решений исходной системы равно

В качестве ещё одного примера рассмотрим известную задачу о беспорядках. Требуется найти число перестановок чисел 1,2,…,n, в которых никакое число i не стоит на i – ом месте. Всего перестановок . Перестановок, в которых числоi стоит на i – ом месте, Перестановок, в которых два различных числаi и j стоят на своих местах, и т.д. По формуле включения и исключения имеем

.

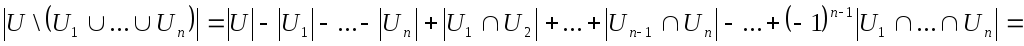
Отметим, что выражение в скобках с ростом стремится к.

Вопросы для самопроверки.

1. В группе 5 студентов не занимается ни в одной спортивной секции, 10 студентов занимается ровно в одной из спортивных секций, 6 судентов ходят в две секции и один студент занимается в трех секциях. Сколько всего студентов в группе?

а) 22; б) 20; в) 25.

2. В группе 25 студентов. Из них в бассейн ходят 10 человек, в гимнастический зал – 8 человек, в волейбольную секцию – 6 человек. При этом 4 человека ходят одновременно в бассейн и на гимнастику, 3 человека – в бассейн и на волейбол и 2 человека – на гимнастику и на волейбол. Один человек ходит во все три секции. Сколько студентов группы не занимается в спортивных секциях?

а) 12; б) 9; в) 11.

3. Сколько натуральных чисел, не превосходящих 100, не делятся на 2 и 3? а) 30; б) 33; в) 34.