!Оптика и квантовая механика / Задачи / 11 / zan14

Занятие 14.

№5.263

Имеется два абсолютно черных источника теплового излучения. Температура одного из них . Найти температуру другого источника, если длина волны, отвечающая максимуму его испускательной способности, на больше длины волны, соответствующей максимуму испускательной способности этого тела.

Решение:

Из закона смещения Вина для различных длин тел: и , тогда

■

№5.264

Энергетическая светимость абсолютно черного тела . Определить длину волны, отвечающей максимуму испускательной способности этого тела.

Решение:

Из закона Стефана-Больцмана:

Из закона смещения Вина: ■

№5.265

Излучение Солнца по своему спектральному составу близко к излучению абсолютно черного тела, для которого максимум испускательной способности приходится на длину волны. Найти массу, теряемую Солнцем ежесекундно за счет этого излучения. Оценить время, за которое масса Солнца уменьшится на 1%.

Решение:

Поскольку излучение Солнца близко к излучению абсолютно черного тела, то из закона смещения Вина: .

Из закона Стефана-Больцмана: .

Тогда найдем энергию, которую излучает Солнце за элементарное время , для этого нам понадобится площадь поверхности Солнца , где его радиус, значит

.

Из релятивистских соображений, убыль энергии Солнца, обусловленная потерей элементарной массы равна:

.

Приравняв выражения для излученной и потраченной на излучение энергии, получим:

,

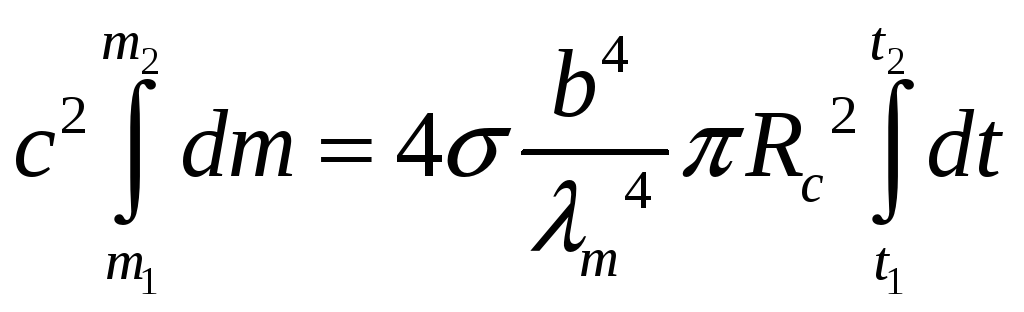
где . Необходимо оценить время, за которое Солнце потеряет 1% своей массы, тогда

,

где текущая масса Солнца, тогда

. ■

№5.267

Медный шарик диаметра поместили в откачанный сосуд, температура стенок которого поддерживается близкой к абсолютному нулю. Начальная температура шарика . Считая поверхность шарика абсолютно черной, найти, через сколько времени его температура уменьшится в раза.

Решение:

Изменение внутренней энергии шарика происходит за счет того, что он излучает. А т.к. стенки сосуда ничего не излучают, шарик ничего не поглощает. Тогда убыль внутренней энергии шарика выглядит следующим образом:

,

где - масса шарика, - удельная теплоемкость меди (ведь наш шарик именно из этого материала), - изменение температуры шарика. Из закона Стефана-Больцмана энергетическая светимость шарика . Зная площадь поверхности шарика можно найти энергию, которую излучает шарик за малый промежуток времени . Учитывая, что площадь поверхности шарика , получим:

Излученная энергия равна убыли внутренней энергии шарика:

.

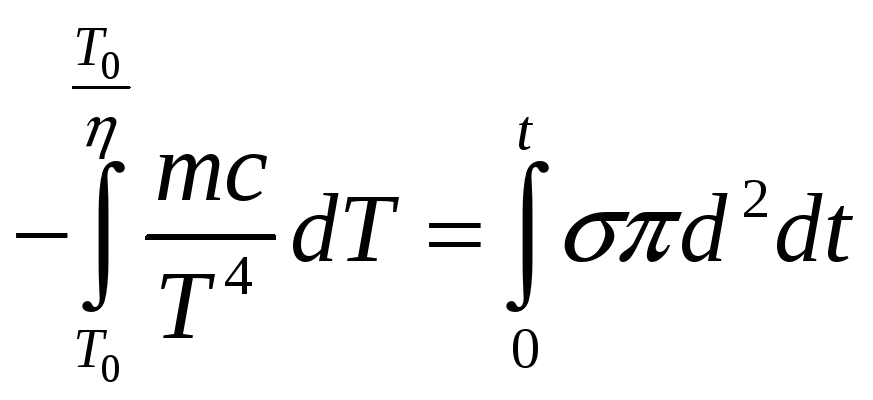
Мы знаем, что , где - плотность меди, тогда . ■

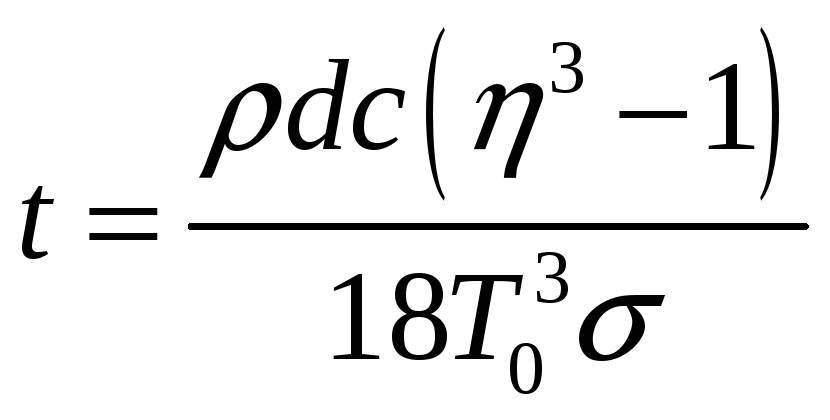№5.268

Т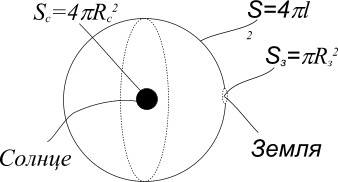емпература поверхности Солнца . Считая, что поглощательная способность Солнца и Земли равна единице и что Земля находится в состоянии теплового равновесия, оценить ее температуру.

Решение:

Из закона Стефана-Больцмана энергетическая светимость Солнца . Тогда Земля поглотит ту часть энергии, излучаемой Солнцем, которая приходится на телесный угол , в пределах которого Землю видно с Солнца:

,

где - энергия, достигшая Земли; - полная энергия, излучаемая поверхностью Солнца за элементарное время, - полный телесный угол. По определению,

,

где - расстояние от Земли до Солнца. Тогда за элементарное время Земля получит энергию:

.

Энергию, излучаемую всей поверхностью Солнца, можно найти по формуле:

,

тогда энергия, поглощаемая Землей за элементарное время равна:

.

Энергия, излучаемая Землей за этот же промежуток времени , из закона Стефана-Больцмана равна:

.

Так как Земля находится в состоянии теплового равновесия, то поглощаемая энергия равна излучаемой, тогда

. ■

№5.270

Полость объемом заполнена тепловым излучением при температуре . Найти:

а) теплоемкость ; б) энтропию этого излучения.

Решение:

а) По определению, теплоемкость - это

,

где - это энергия теплового излучения. Энергетическая светимость , где - плотность энергии теплового излучения. Так как полость равномерно заполнена излучением, то , тогда

.

Дифференцируя это выражение по , получаем:

■

б) Приращение энтропии:

,

так как объем остается постоянным, то , тогда

. ■

№5.275

Найти с помощью формулы Планка мощность излучения единицы поверхности абсолютно черного тела, приходящегося на узкий интервал длин волн вблизи максимума спектральной плотности излучения, при температуре тела .

Решение:

Поток энергии испускаемый единицей поверхности тела (энергетическая светимость тела) в интервале длин волн равняется , где - испускательная способность тела. Нас интересует интервал длин волн шириной , тогда

.

Энергетическая светимость абсолютно черного тела и плотность энергии излучения связаны соотношением: , так как это равенство должно выполнятся для каждой спектральной составляющей излучения, то

.

Воспользуемся формулой Планка:

.

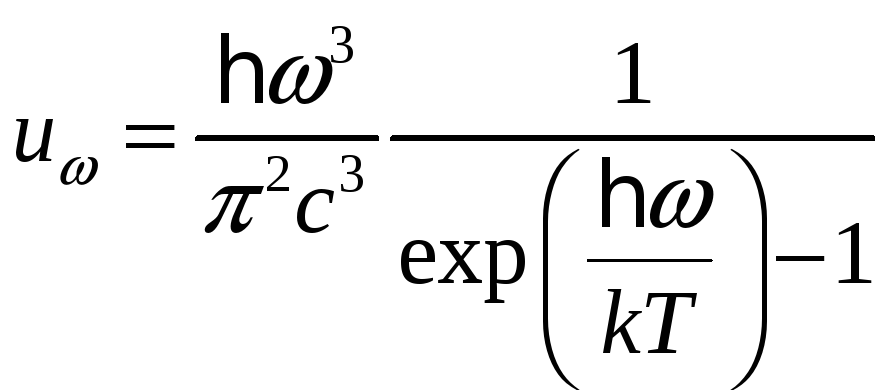Зная, как выражается частота через длину волны излучения (), получим:

.

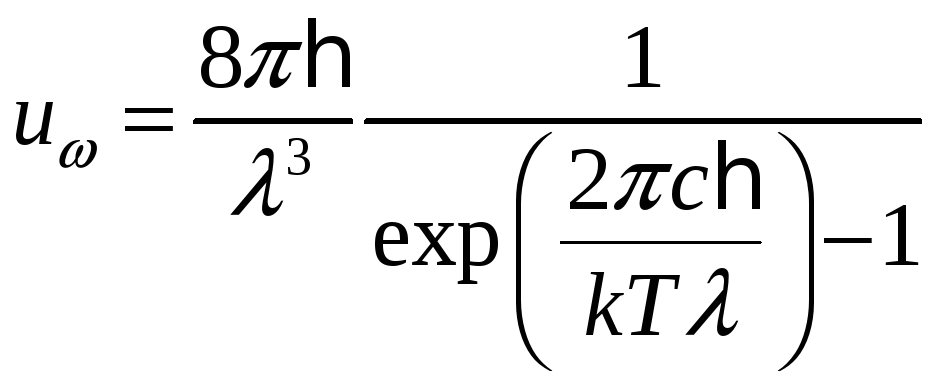Мы знаем, что , из формулы Планка получим:

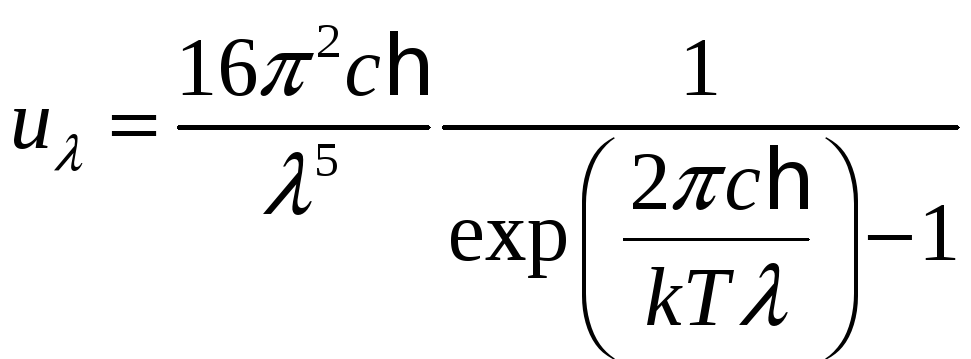
Поскольку мы рассматриваем узкий интервал длин воли вблизи максимума спектральной плотности изучения, то из закона смещения Вина:

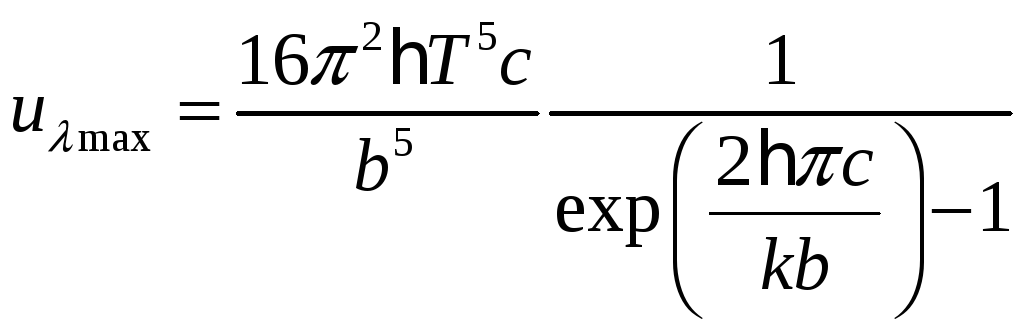
Таким образом, мы получили искомую максимальную плотность энергии излучения, тогда

■
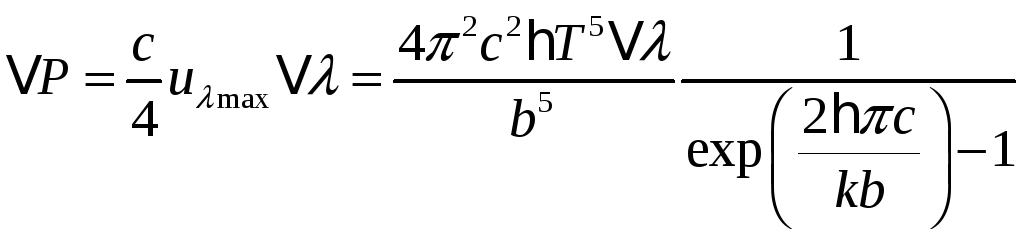