
!Оптика и квантовая механика / Задачи / 11 / zan23_24
.docЗанятия 23,24.
№ 6.113.
Найти возможные
значения полных механических моментов
атомов, находящихся в состояниях
![]() и
и
![]() .
.
Решение:
Полный механический момент атома находится по формуле:
![]() ,
,
где
![]() может принимать значения от
может принимать значения от
![]() до
до
![]() .
В первом случае (для атома, находящегося
в состоянии
.
В первом случае (для атома, находящегося
в состоянии
![]() ),
из общего обозначения
),
из общего обозначения
![]() находим:
находим:
![]() .
.
Тогда
![]() может принимать значения:
может принимать значения:
![]() ,
,
тогда полный механический момент может быть равен:
![]() .
.
Аналогично для атома, находящегося в
состоянии
![]() ,
получаем:
,
получаем:
![]() .
.
![]() может принимать значения:
может принимать значения:
![]() ,
,
тогда полный механический момент может быть равен:
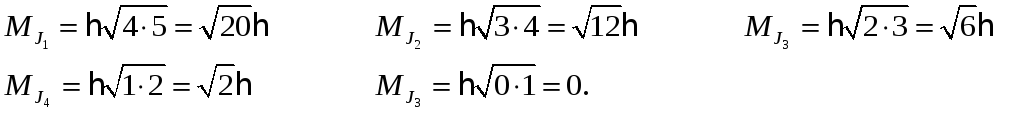
№ 6.116.
Атом находится в
состоянии, мультиплетность которого
равна трем, а полный механический момент
![]() .
Каким может быть соответствующее
квантовое число
.
Каким может быть соответствующее
квантовое число
![]() ?
?
Решение:
Полный механический момент атома находится по формуле:
![]()
![]()
![]() .
.
По определению, мультиплетность атома
![]() ,
тогда
,
тогда
![]()
![]()
![]() .
.
Вспомним, что представляет из себя
спектр значений
![]() :
:
![]() .
.
Из первого значения
![]() ,
получаем:
,
получаем:
![]()
![]()
![]() .
.
Рассмотрим последнее значение
![]() :
:
![]()
![]()
![]() ,
,
но т.к.
![]() может принимать только положительные
значения,
может принимать только положительные
значения,
![]() .
Очевидно,
.
Очевидно,
![]() может принимать и все промежуточные
значения между полученными нами крайними
значениями:
может принимать и все промежуточные
значения между полученными нами крайними
значениями:
![]() .
.
№ 6.117.
Определить
максимально возможный орбитальный
механический момент атома в состоянии,
мультиплетность которого равна пяти и
кратность вырождения по
![]() - семи. Написать спектральное обозначение
соответствующего терма.
- семи. Написать спектральное обозначение
соответствующего терма.
Решение:
По определению, кратность вырождения
по
![]() равна:
равна:
![]()
![]()
![]() .
.
По определению мультиплетности,
![]()
![]()
![]() .
.
Теперь легко найти максимальное значение
![]() из условия:
из условия:
![]()
![]()
![]() .
.
Тогда максимально возможный орбитальный механический момент равен:
![]() .
.
Спектрально обозначение соответствующего терма будет выглядеть следующим образом:
![]()
№ 6.122.
Установить, какие из нижеперечисленных переходов запрещены правилами отбора:
Решение:
Вспомним правила отбора:
![]()
![]()
![]() .
.
-
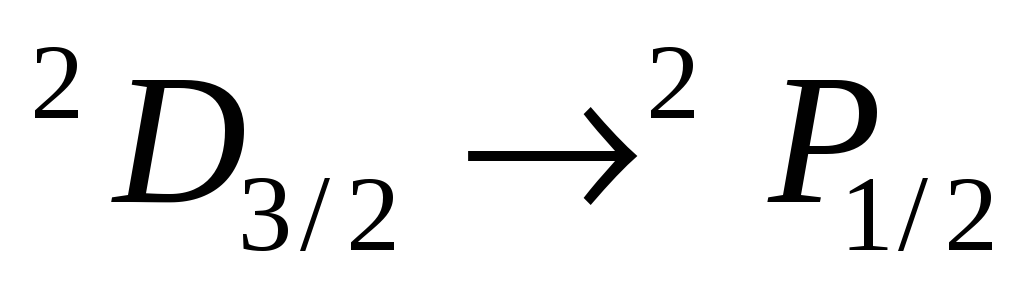 -
возможен:
-
возможен:
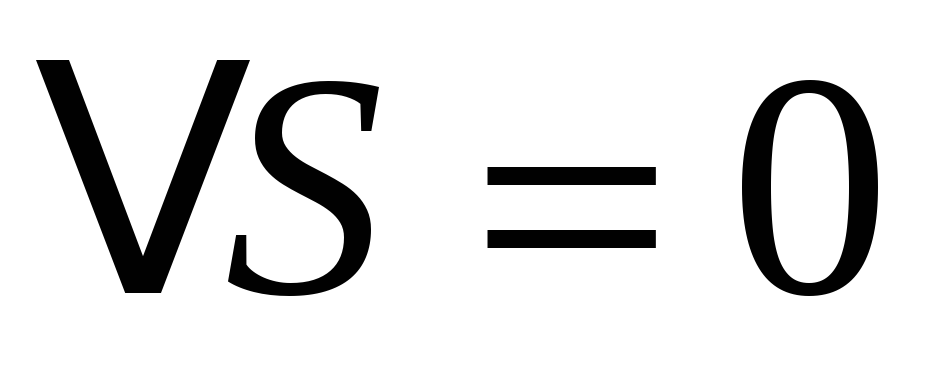 ,
,
 ,
,
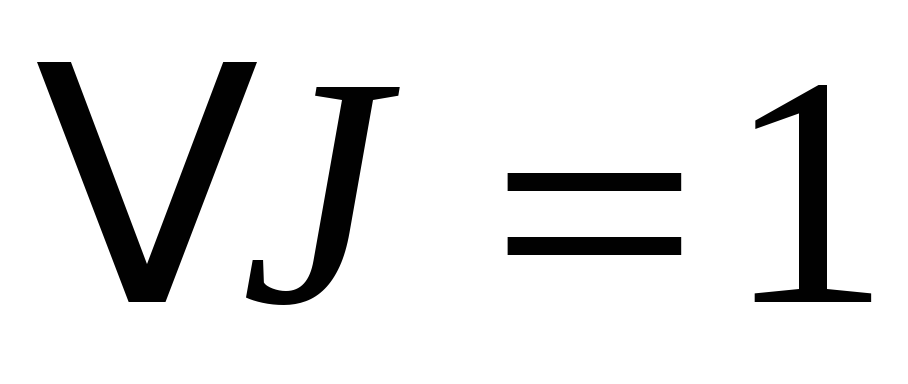 ;
; -
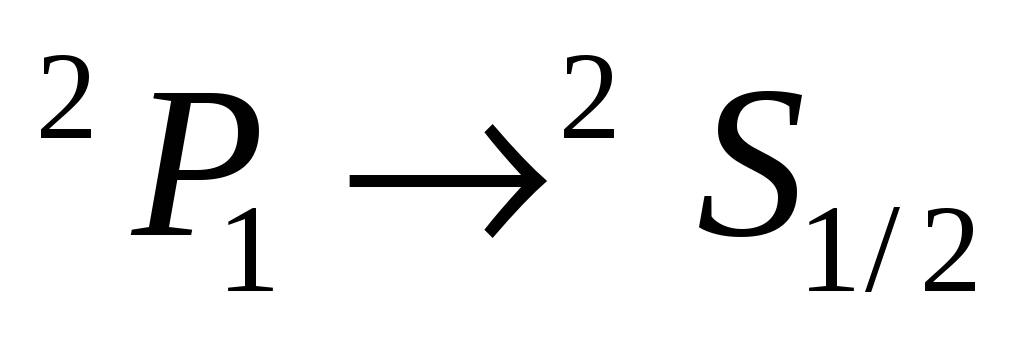 -
невозможен:
-
невозможен:
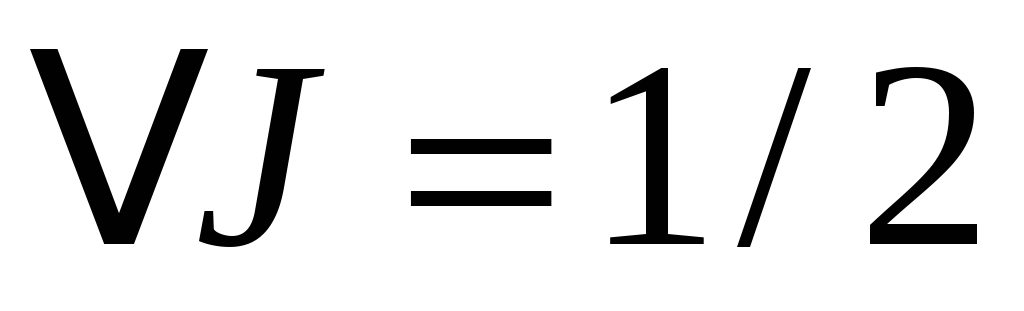 ;
; -
 -
невозможен:
-
невозможен:
 ;
; -
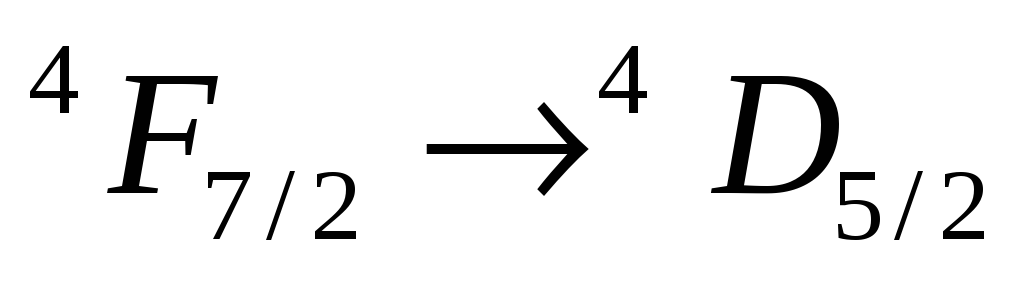 -
возможен:
-
возможен:
 ,
,
 ,
,

№ 6.123.
Определить суммарную
кратность вырождения
![]() -
состояния атома лития. Каков физический
смысл этой величины?
-
состояния атома лития. Каков физический
смысл этой величины?
Решение:
В задаче зафиксированы n
и l квантовые числа.
Значит, данное состояние будет вырождено
по
![]() и
и
![]() .
Иными словами, суммарная кратность
вырождения в нашем случае равна:
.
Иными словами, суммарная кратность
вырождения в нашем случае равна:
![]() ,
,
поскольку если указан спин, то его
проекция может принимать
![]() значений; если указан
значений; если указан
![]() ,
то его проекция может принимать
,
то его проекция может принимать
![]() значений. В нашей задаче
значений. В нашей задаче
![]() (поскольку атом лития имеет один
электрон),
(поскольку атом лития имеет один
электрон),
![]() .
Итак, имеем:
.
Итак, имеем:
![]()
![]() .
.
Тогда суммарная кратность вырождения равна:
![]()
№ 6.160.
Некоторый атом
находится в состоянии, для которого
![]() ,
полный механический момент
,
полный механический момент
![]() ,
а магнитный момент равен нулю. Написать
спектральный символ соответствующего
терма.
,
а магнитный момент равен нулю. Написать
спектральный символ соответствующего
терма.
Решение:
По условию, магнитный момент
![]() :
:
![]() .
.
Поскольку для полного механического момента имеем:
![]()
![]()
![]() ,
,
значит
![]() .
Приравняв фактор Ланде к нулю, получим:
.
Приравняв фактор Ланде к нулю, получим:
![]()
![]()
![]() .
.
Спектральный символ соответствующего
терма, для которого
![]() ,
,
![]() ,
,
![]() ,
имеет вид:
,
имеет вид:
![]()
№ 6.164.
Узкий пучок атомов
ванадия в основном состоянии
![]() пропускают по методу Штерна и Герлаха
через поперечное резко неоднородное
магнитное поле протяженностью
пропускают по методу Штерна и Герлаха
через поперечное резко неоднородное
магнитное поле протяженностью
![]() .
Расщепление пучка наблюдают на экране,
отстоящем от магнита на расстояние
.
Расщепление пучка наблюдают на экране,
отстоящем от магнита на расстояние
![]() .
Кинетическая энергия атомов
.
Кинетическая энергия атомов
![]() .
При каком значении градиента индукции
.
При каком значении градиента индукции
![]() магнитного поля расстояние между
крайними компонентами расщепленного
пучка на экране будет составлять
магнитного поля расстояние между
крайними компонентами расщепленного
пучка на экране будет составлять
![]() .
.
Решение:
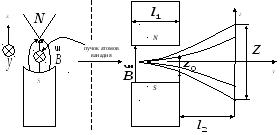
Схема опыта Штерна и Герлаха изображена на правой части рисунка. Теория говорит нам о том, что на нейтральные частицы, движущиеся в неоднородном поле, действует сила, направленная в сторону большей неоднородности (неоднородность поля достигается при помощи полюсов специальной формы, см. левую часть рисунка). Таким образом, частицы приобретают дополнительную энергию:
![]() .
.
Как известно, сила, действующая на частицы, может быть найдена по формуле
![]() .
.
Заметим, что в области неоднородности
поля, между полюсами магнита, отлична
от нуля только
![]() компонента
поля, тогда
компонента
поля, тогда
![]()
![]()
![]() ,
,
где
![]() - собственное значение оператора
- собственное значение оператора
![]() ,
может принимать значения от
,
может принимать значения от
![]() до
до
![]() .
Поскольку мультиплет атомов Ванадия
(по условию) -
.
Поскольку мультиплет атомов Ванадия
(по условию) -
![]() ,
где
,
где
![]() ,
пучок расщепится на 4 составляющие (
,
пучок расщепится на 4 составляющие (![]() ),
крайние составляющие будут, очевидно,
образованы пучками с
),
крайние составляющие будут, очевидно,
образованы пучками с
![]() и
и
![]() (т.е.
(т.е.
![]() ),
поскольку
),
поскольку
![]() .
.
Т.к. сила, действующая на каждую из
составляющих пучка, постоянна, движение
частицы в области между полюсами магнита
(вдоль оси
![]() )
является равноускоренным, при вылете
из области
)
является равноускоренным, при вылете
из области
![]() частица будет обладать
частица будет обладать
![]() составляющей
скорости
составляющей
скорости
![]() ,
где
,
где
![]() ,
,
![]() - отклонение частиц на участке
- отклонение частиц на участке
![]() .
На участке
.
На участке
![]() движение вдоль оси
движение вдоль оси
![]() является равномерным. Общее отклонение
частиц от начального направления
движения складывается из отклонений,
приобретенных на участках
является равномерным. Общее отклонение
частиц от начального направления
движения складывается из отклонений,
приобретенных на участках
![]() и
и
![]() :
:
![]()
![]()
![]()
![]()
![]() ,
,
где
![]() - проекция скорости движения частиц на
ось
- проекция скорости движения частиц на
ось
![]() ,
,
![]() - время движения частиц на участке
- время движения частиц на участке
![]() .
Т.к.
.
Т.к.
![]() составляющая
поля отсутствует, движение вдоль оси
составляющая
поля отсутствует, движение вдоль оси
![]() является равномерным на протяжение
всего движения частицы, тогда
является равномерным на протяжение
всего движения частицы, тогда

![]()
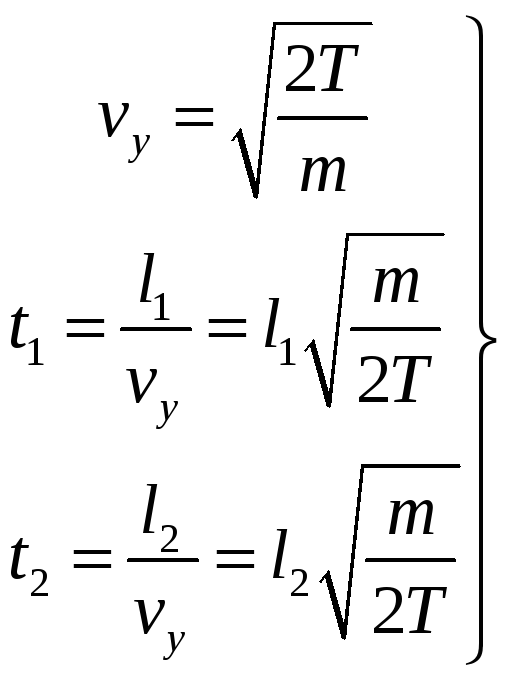 .
.
Подставляя все полученные результаты в выражение для общего смещения, получим:
![]()
![]()
![]()
![]()
![]() .
.
Подставляя в выражение для проекции
силы на ось
![]() ,
получим:
,
получим:
![]()
![]()
![]() .
.
№ 6.165.
На сколько подуровней расщепится в слабом магнитном поле терм:
Решение:
-
 ;
;
В общем случае, терм
![]() расщепляется на состояния с различными
расщепляется на состояния с различными
![]() ,
всего
,
всего
![]() состояний, за исключением случаев, когда
фактор Ланде = 0. Энергия взаимодействия
атома с внешним полем описывается
уравнением:
состояний, за исключением случаев, когда
фактор Ланде = 0. Энергия взаимодействия
атома с внешним полем описывается
уравнением:
![]() ,
, ![]() ,
где
,
где
![]() .
.
Итак, терм
![]() не расщепляется, поскольку
не расщепляется, поскольку
![]() .
.
-
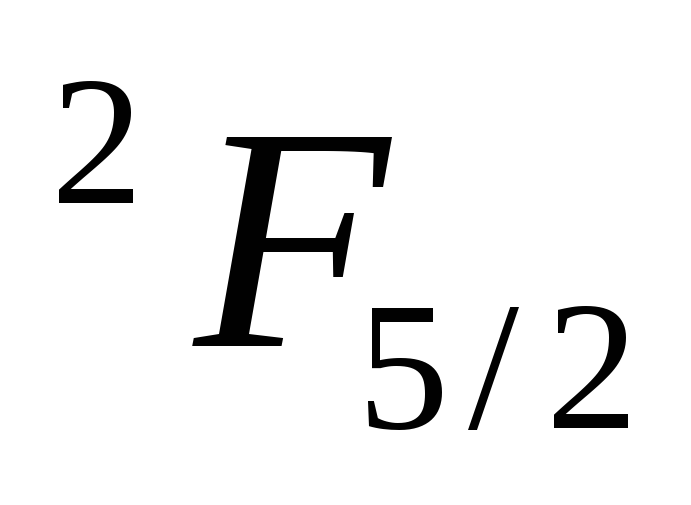 ;
;
Т.к. в случае, когда фактор Ланде равен нулю, терм не расщепляется, найдем фактор Ланде:
 ,
,
значит терм расщепляется на
![]() подуровней.
подуровней.
-
 ;
;
Т.к. в случае, когда фактор Ланде равен нулю, терм не расщепляется, найдем фактор Ланде:
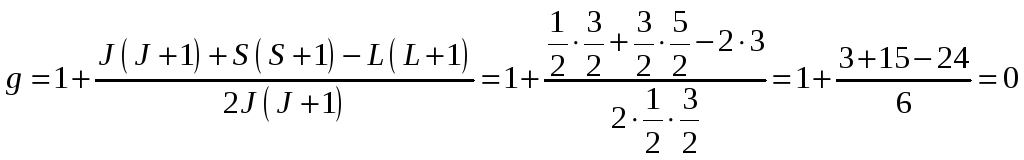 ,
,
значит терм не расщепляется.
№ 6.169.
Известно, что
спектральная линия
![]() атома обусловлена переходом между
синглетными термами. Вычислить интервал
атома обусловлена переходом между
синглетными термами. Вычислить интервал
![]() между крайними компонентами этой линии
в магнитном поле с индукцией
между крайними компонентами этой линии
в магнитном поле с индукцией
![]() .
.
Решение:
С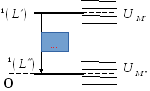 инглетным
называется терм, у которого
инглетным
называется терм, у которого
![]() ,
и, следовательно,
,
и, следовательно,
![]() и фактор Ланде
и фактор Ланде
![]() (в этом легко убедиться). Схема образования
спектральных линий при переходе между
синглетными термами в магнитном поле
изображена на рисунке. При погружении
в магнитное поле частицы приобретают
дополнительную энергию
(в этом легко убедиться). Схема образования
спектральных линий при переходе между
синглетными термами в магнитном поле
изображена на рисунке. При погружении
в магнитное поле частицы приобретают
дополнительную энергию
![]() и происходит расщепление уровней по
и происходит расщепление уровней по
![]() :
:
![]() ,
,
где
![]() может принимать значения от
может принимать значения от
![]() до
до
![]() (или в случае синглетного терма, от
(или в случае синглетного терма, от
![]() до
до
![]() ).
Если взять за нулевой уровень энергии
).
Если взять за нулевой уровень энергии
![]() ,
то относительно этого уровня, энергия
,
то относительно этого уровня, энергия
![]() ,
,
![]() .
.
В дальнейшем будем опускать фактор Ланде, поскольку он равен единице. Тогда спектральные линии, обусловленные переходами между этими энергиями, равны:
![]()
![]()
![]() .
.
По правилу отбора для проекции полного
момента,
![]() ,
тогда
,
тогда
![]() ,
, ![]() .
.
Найдем разность длин волн между этими спектральными линиями:
![]()
![]()
![]()
![]()

![]()
![]() .
.
№ 6.173.
Длины волн дублета
желтой линии натрия
![]() равны
равны
![]() и
и
![]() нм. Найти:
нм. Найти:
а) отношение
интервалов между соседними подуровнями
зеемановского расщепления термов
![]() и
и
![]() в слабом магнитном поле;
в слабом магнитном поле;
б) индукцию
![]() магнитного поля, при которой интервал
между соседними подуровнями зеемановского
расщепления терма
магнитного поля, при которой интервал
между соседними подуровнями зеемановского
расщепления терма
![]() будет в
будет в
![]() раз меньше естественного расщепления
терма
раз меньше естественного расщепления
терма
![]() .
.
Решение:
а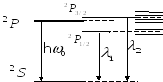 )
Схема перехода
)
Схема перехода
![]() изображена на рисунке. Как известно,
подуровень
изображена на рисунке. Как известно,
подуровень
![]() (
(![]() подуровень)
не расщепляется. В слабом магнитном
поле частицы приобретают дополнительную
энергию
подуровень)
не расщепляется. В слабом магнитном
поле частицы приобретают дополнительную
энергию
![]() .
.
Поскольку нас интересует отношение интервалов между соседними подуровнями зеемановского расщепления, то для данного мультиплета:

![]()
![]() .
.
Тогда искомое отношение имеет вид:
![]() .
.
Найдем факторы Ланде для
![]() и
и
![]() :
:
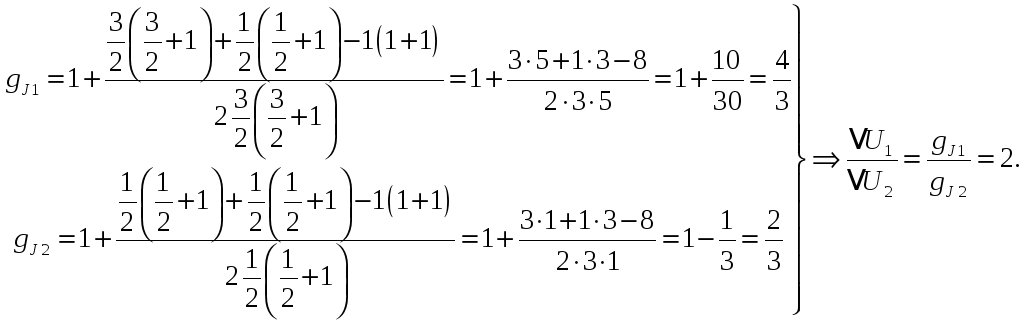
б) По условию,
![]() .
Как было найдено в пункте а) , интервал
между соседними подуровнями зеемановского
расщепления терма
.
Как было найдено в пункте а) , интервал
между соседними подуровнями зеемановского
расщепления терма
![]() имеет вид:
имеет вид:
![]() ,
,
где в данном случае
![]() .
Тогда
.
Тогда
![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
