!Оптика и квантовая механика / Задачи / 11 / zan18_19

Занятия 18, 19.

№6.50

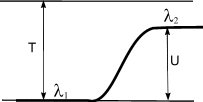
Частица движется слева направо в одномерном потенциальном поле, показанном на рисунке. Левее барьера, высота которого , кинетическая энергия частицы . Во сколько раз и как изменится дебройлевская длина волны при переходе через барьер? Решение:

Так как , барьер является низким, и можно найти дебройлевские длины волн и до и после барьера соответственно. Полная же энергия частицы до барьера равна ее кинетической энергии. Тогда получаем:

и , где и , тогда  №6.51

Какую энергию необходимо сообщить электрону, чтобы его дебройлевская длина волны уменьшилась от 100 до 50пм?

Решение: Электрон обладает энергией , тогда для данных длин волн: , .

Следовательно, 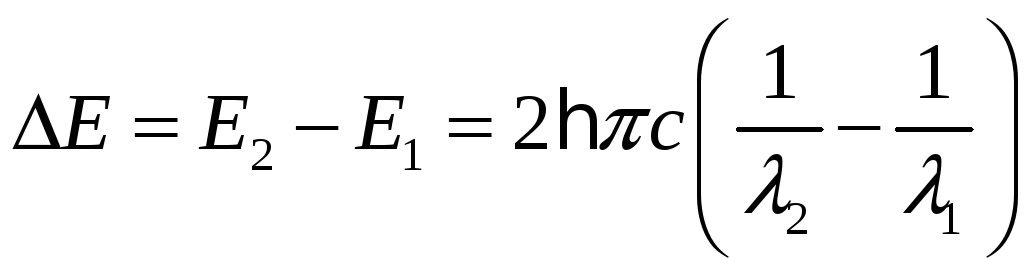.  №6.52

Нейтрон с кинетической энергией налетает на покоящийся дейтрон (ядро тяжелого водорода). Найти дебройлевские длины волн обеих частиц в системе отсчета их центра масс.

Решение: Перейдем в систему отсчета, связанную с центром масс системы частиц (Ц–систему). Пусть скорость центра масс = , тогда из классической механики:

или .

(После получения результата мы проверим, должны ли пользоваться релятивистскими формулами). По определению дебройлевской длины волны, длины волн частиц в Ц-системе будут выглядеть следующим образом:

и .

Поскольку дейтрон покоится, то в системе центра масс: ,а . Т.к. суммарный импульс системы в Ц–системе = 0, импульсы частиц будут одинаковы:

.

Учитывая, что , получаем , найдем искомые длины волн:

. 

Убедимся, что в условиях данной задачи нет смысла пользоваться релятивистскими формулами. Действительно, для скорости нейтрона имеем следующее выражение:

- значительно меньше скорости света. 

№6.57

При каком значении кинетической энергии дебройлевская длина волны электрона равна его комптоновской длине волны?

Решение:

Длина волны де Бройля: ; длина волны Комптона: .

Очевидно, из сравнения этих формул вытекает, что импульс электрона должен быть равен:

.

Т.к. скорость частицы равна скорости света, имеем дело с релятивистской частицей. Тогда для кинетической энергии электрона, имеем:

.  №6.58

Найти дебройлевскую длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра .

Решение: Причина рентгеновского спектра: электрон, подлетая к антикатоду, тормозит, т.е. движется с ускорением. А любая частица, движущаяся с ускорением, излучает. Причем длину волны коротковолновой границы будем наблюдать в том случае, когда электрон затормозит перед самой границей антикатода. Значит, кинетическая энергия электронов в трубке:

,

где - коротковолновая граница рентгеновского спектра. С другой стороны, кинетическая энергия релятивистской частицы:

.

Приравнивая правые части выражений для энергии и возводя их в квадрат, получим:

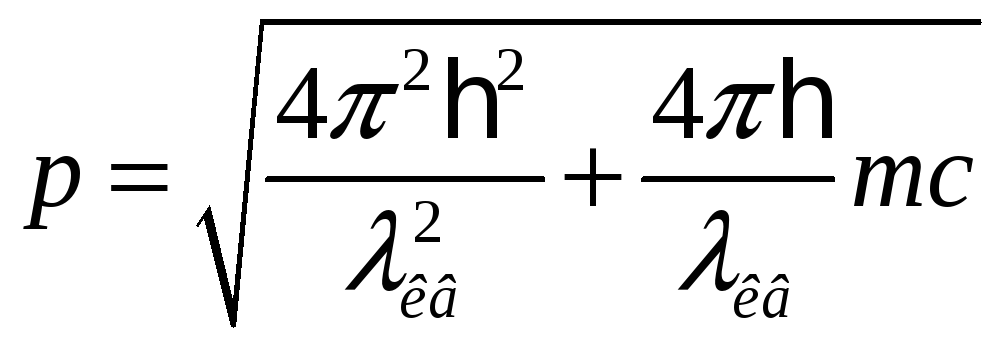
Тогда длина волны де Бройля:

. 

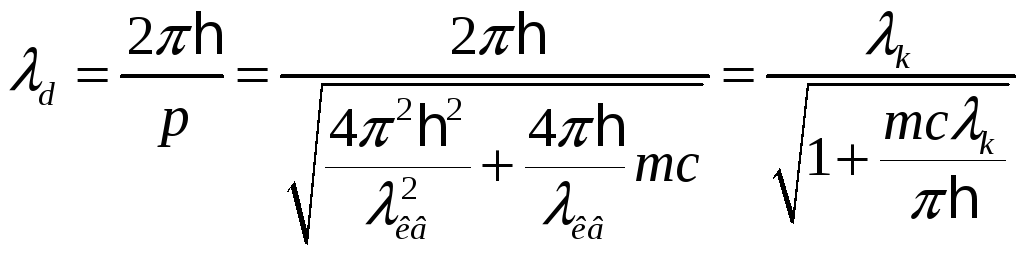№6.59

Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины . Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние , ширина центрального дифракционного максимума .

Решение: Условие минимума для дифракции Фраунгофера на щели: , нас интересует . Тогда . Т.к. угол можно считать малым, то и (т.к. ширина главного максимума равна удвоенному расстоянию от центра до первого минимума). С другой стороны:

. Следовательно, . 

№6.60

Параллельный пучок электронов, ускоренных разностью потенциалов , падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми . Определить расстояние между соседними максимума дифракционной картины на экране, расположенном на расстоянии от щелей.

Решение: Так как электроны ускоряются разностью потенциалов, то => Из условия максимума на решетке: , где нас интересует . Из-за малости углов можно считать: и . Вспоминаем результат, полученный при изучении схемы Юнга:

Тогда учитывая, что , получим:  №6.63

Узкий пучок электронов с кинетической энергией проходит через поликристаллическую фольгу, образуя на экране систему дифракционных колец. Вычислить межплоскостное расстояние, соответствующее отражению третьего порядка от некоторой системы кристаллических плоскостей, если ему отвечает дифракционное кольцо диаметра . Расстояние между экраном и фольгой .

Решение: Дифракционная картина на экране будет возникать из-за накопления разности хода между лучами, отраженными от атомов, расположенных в разных плоскостях кристаллической решетки вещества. Схема образования разности хода показана на правом рисунке. Условие Вульфа-Брэгга для дифракционных максимумов:

,

где d – искомое межплоскостное расстояние. В нашем случае , тогда

Из рисунка видно, что , тогда . Длина волны де Бройля:

,

тогда для межплоскостного расстояния окончательно получаем:



№6.72

Электрон с кинетической энергией локализован в области размером . Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.

Решение: Из соотношения неопределенностей получаем:

Поскольку и , получаем:



№6.73

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы . Оценить с помощью соотношения неопределенностей силу давления электрона на стенки ямы при минимально возможной энергии.

Решение: Давление на стенки ямы образуется из-за столкновения электронов со стенками. Тогда для нахождения силы давления мы можем воспользоваться законом сохранения импульса для электрона. Рассмотрим абсолютно упругий удар электрона о стенку (яма одномерная, поэтому записываем сразу в проекции на направление х):

.

При ударе импульс по модулю остается прежним, но меняет направление на противоположное, тогда . Для нахождения , воспользуемся соотношением неопределенностей. Полная энергия электрона в яме описывается выражением:

,

где в яме . Т.к. в условии сказано, что электрон обладает минимально возможной энергией, формальным минимумом выражения является . Тогда из закона сохранения импульса следует:

Из соотношениям неопределенностей имеем:

.

Т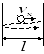еперь оценим время между двумя столкновениями. Если электрон движется со скоростью , то между двумя ближайшими столкновениями об один фиксированный участок стенки пройдет время (см. рисунок):

,

где мы воспользовались нерелятивистской формулой для импульса: . Из механики известно, что , тогда



№6.75

Частица массой движется в одномерном потенциальном поле (гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.

Решение: Полная энергия электрона в одномерном потенциальном поле описывается выражением:

.

Формальному минимуму этого выражения, очевидно, будут соответствовать следующие значения импульса и координаты:

, .

Тогда из соотношений:

.

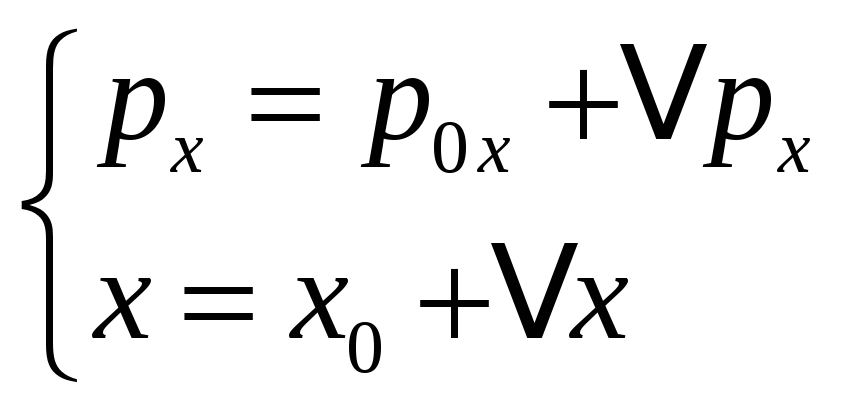
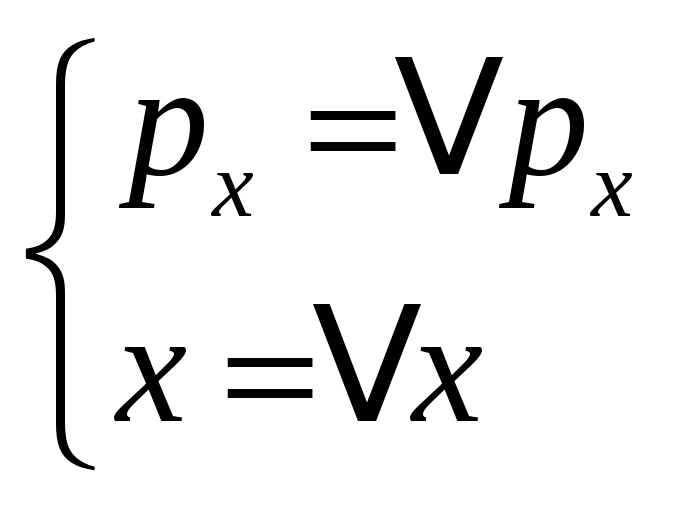Из соотношения неопределенностей, .

Тогда выражение для энергии приобретает следующий вид:

.

Продифференцируем для отыскания минимума функции:

Тогда подставив это значение в выражение для энергии, получим:

. 

№6.76

Оценить с помощью соотношения неопределенностей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.

Решение: Для энергии электрона, движущегося в потенциальном поле ядра атома, имеем:

,

Из соотношения неопределенностей, для получения значения минимальной энергии (см. предыдущую задачу) , тогда:

.

Продифференцируем для нахождения минимума:

.

Подставив в функцию для энергии, получим:

. 