!Оптика и квантовая механика / Задачи / 11 / zan13

Занятие 13.

№5.215

Свободный электрон находится в поле монохроматической световой волны. Интенсивность света , его частота . Найти:

А) амплитуду колебаний электрона и амплитуду его скорости;

Б) отношение , где и - амплитудные значения сил, действующих на электрон со стороны магнитной и электрической составляющих поля световой волны; показать также, что это соотношение равно , где -амплитуда скорости электрона, - скорость света.

Указание: В уравнении движения электрона можно не учитывать действие магнитной составляющей поля (как будет видно из расчета, оно пренебрежимо мало). В уравнении движения электрона можно не учитывать действие магнитной составляющей поля(составляющих поля свет00000000000000000

Решение:

А) Электрон совершает движение за счет электрической силы со стороны поля световой волны, тогда из второго закона Ньютона , где .

Тогда для малого промежутка времени получаем: .

Для получения выражения для радиус-вектора электрона проинтегрируем это равенство:

Выразим через интенсивность:

, где - вектор Пойнтинга.

Из равенства , учитывая, что в нашем случае , следует, что 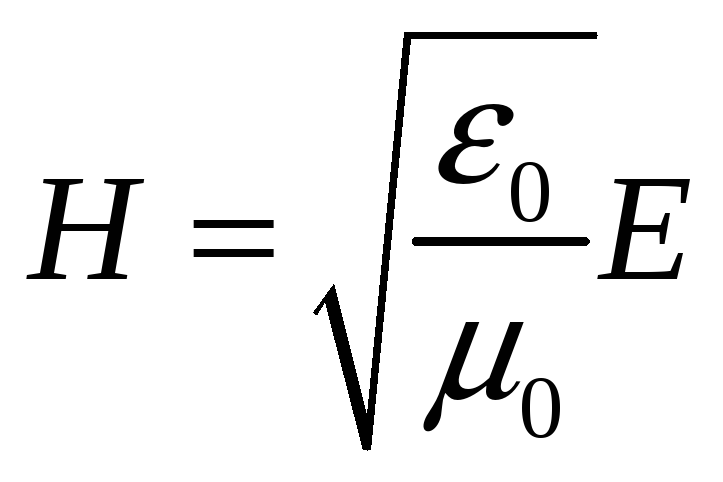. Тогда для интенсивности окончательно получаем, что .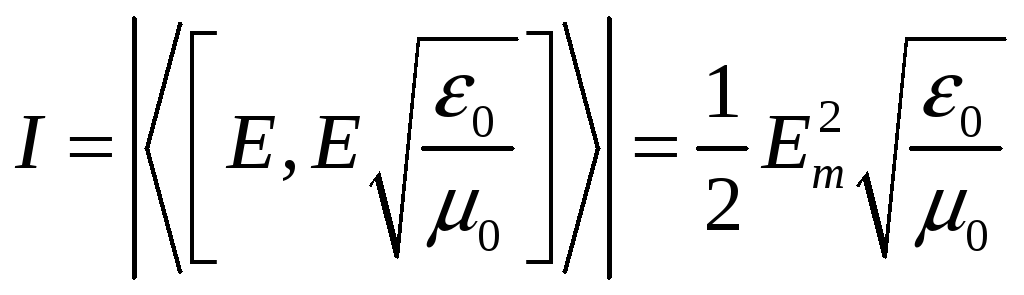

Зная, что , получаем .

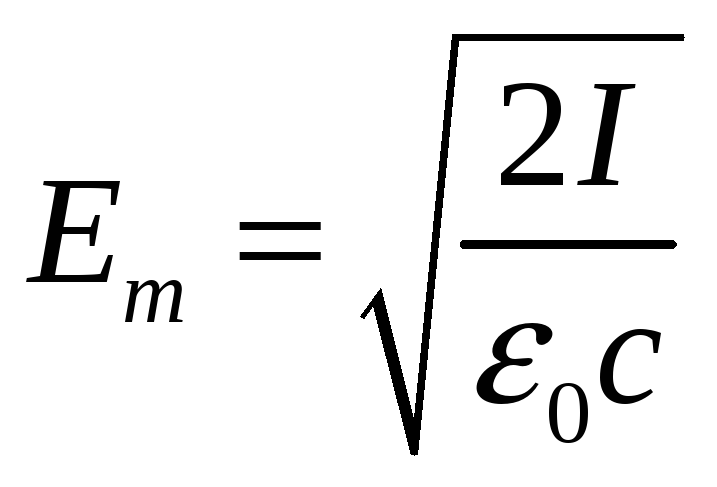Наконец подставим для получения окончательного ответа

и ■

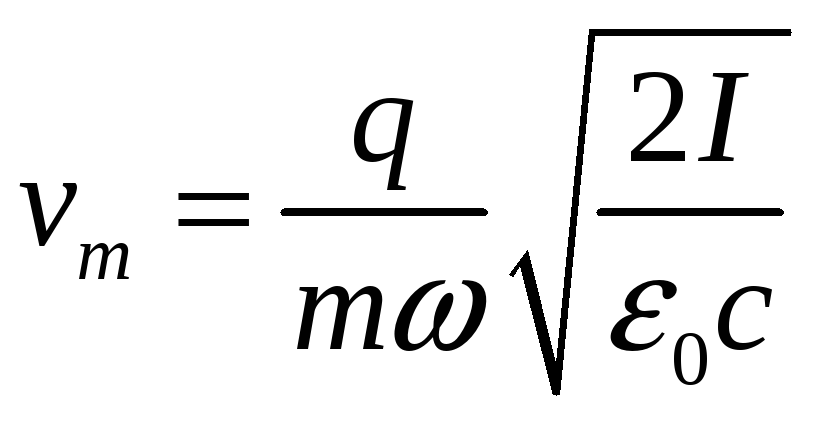№5.216

Электромагнитная волна с частотой распространяется в разреженной плазме. Концентрация свободных электронов в плазме равна . Пренебрегая взаимодействием волны с ионами плазмы, найти зависимость:

А) диэлектрической проницаемости плазмы от частоты;

Б) фазовой скорости от длины волны в плазме.

Решение:

А) Поскольку плазма разреженная, то электроны свободны и на них не действует квазиупругая возвращающая сила , тогда согласно элементарной теории дисперсии из получаем ■

Б) Как известно , также .

Элементарными преобразованиями получаем 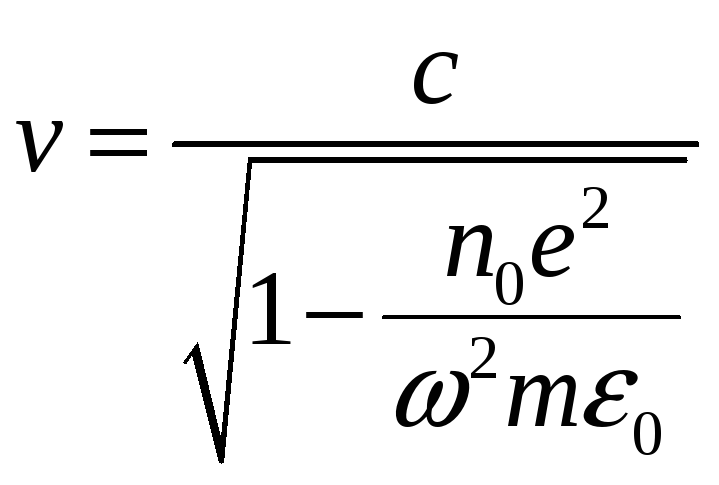, где ■

№5.217

Найти концентрацию свободных электронов ионосферы, если для радиоволн с частотой ее показатель преломления .

Решение:

По аналогии с предыдущей задачей, так как все электроны свободные, то . Таким образом , откуда легко получить, что ■

№5.218

Имея в виду, что для достаточно жестких рентгеновских лучей электроны вещества можно считать свободными, определить, на сколько отличается от единицы показатель преломления графита для рентгеновских лучей с длиной волны в вакууме .

Решение:

Поскольку электроны свободные, то опять же получаем, что .

Нам надо сравнить показатель преломления с единицей, тогда ,

Из-за малости второго слагаемого под корнем можно упростить,

■

№5.231

Монохроматический пучок света падает нормально на поверхность плоскопараллельной пластины толщины . Показатель поглощения вещества пластины линейно изменяется вдоль нормали к ее поверхности от значения до . Коэффициент отражения от каждой пластины равен . Пренебрегая вторичными отражениями, определить коэффициент пропускания пластины.

Решение:

Разделим пластину на тонкие слои, в пределах которых показатель поглощения можно считать постоянным. Рассмотрим один из таких слоев от до .

Убыль интенсивности в этом слое , где , так как показатель поглощения линейно изменяется от до .

Тогда мы можем проинтегрировать по всей толщине пластины

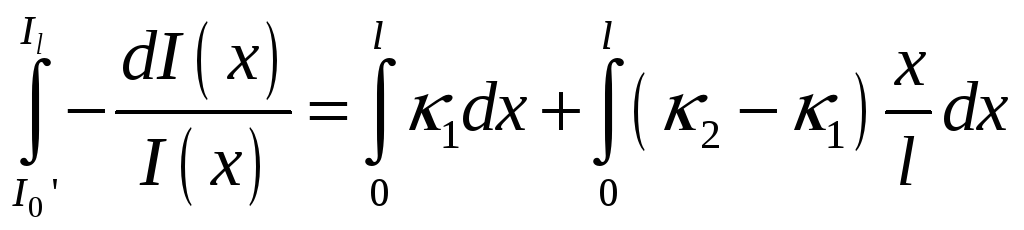
Так как коэффициент отражения равен , но вторичными отражениями нужно пренебречь, то внутрь пластины пройдет волна с интенсивностью и потери на отражении будут только при выходе волны из пластины.

Тогда интегрируя получаем ,что

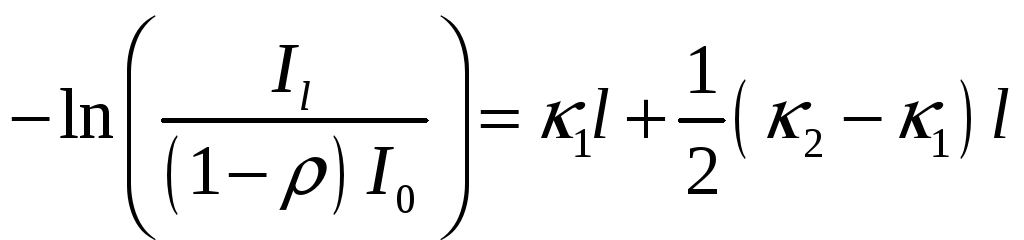
Учитывая, что при выходе мы теряем на отражении получаем, что

■

№5.235

Во сколько раз уменьшится интенсивность узкого пучка рентгеновского излучения с длиной волны при прохождении свинцовой пластинки толщины , если массовый показатель ослабления для данной длины волны ?

Решение:

Воспользуемся результатом предыдущей задачи, учтя, что в данном случае показатель ослабления не меняется с толщиной ( , где -это плотность свинца) и потерь при отражении нет (), тогда получим, что ■