!Оптика и квантовая механика / Задачи / 11 / zan03_04

Занятия 3,4.

№5.83

На тонкую пленку (n=1.33) падает параллельный пучок белого света. Угол падения . При какой толщине пленки зеркально отраженный свет будет наиболее сильно окрашен в желтый цвет (мкм)?

Решение:

Наиболее яркий окрас в желтый свет говорит о том, что отражаться будет свет с длиной волны мкм. И в условие максимумов нужно подставить именно это значение. Условие максимумов при интерференции света, отраженного от тонкой пластинки толщины b:

,

где - угол падения, k –целое число. Тогда

■

№5.85

Для уменьшения потерь света из-за отражения от поверхности стекла последнее покрывают тонким слоем вещества с показателем преломления , где n показатель преломления стекла. В этом случае амплитуды световых колебаний, отраженных от обеих поверхностей такого слоя, будут одинаковыми. При какой толщине этого слоя отражательная способность стекла в направлении нормали будет равна нулю для света с длиной волны ?

Р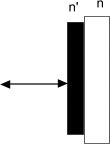ешение:

Угол падения равен 0, поэтому проходящий луч не преломляется. Из условия минимумов

.

Так как ,

,

где - оптическая разность хода. Приравнивая выражения для , получим:

, k=0,1,2…. ■

№5.86

Рассеянный монохроматический свет с =0,60 мкм падает на тонкую пленку вещества с показателем преломления n=1,5. Определить толщину пленки, если угловое расстояние между соседними максимумами, наблюдаемыми в отраженном свете под углами с нормалью, близкими к , равно .

Решение:

У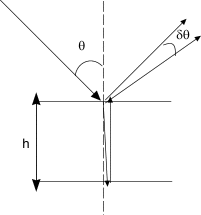словие максимумов при интерференции света, отраженного от тонкой пластинки толщины :

Где - угол падения, –целое число. Из условия расстояния между двумя максимумами получаем:

Найдем разность двух корней

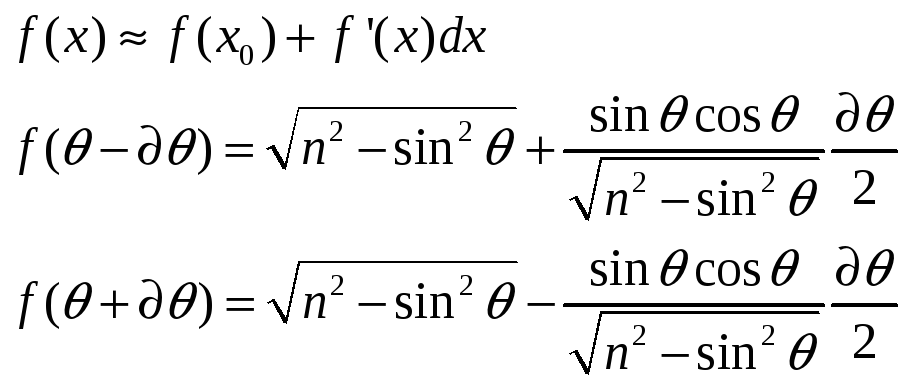
Подставив эти значения в расстояние между максимумами, получим:

. ■

№5.88

П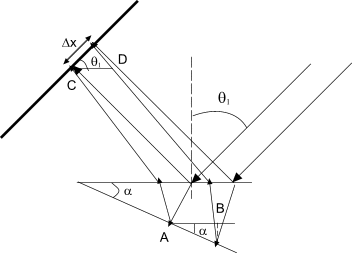лоская монохроматическая световая волна длины падает на поверхность стеклянного клина, угол между гранями которого . Плоскость падения перпендикулярна к ребру клина, угол падения . Найти расстояние между соседними максимумами интерференционных полос на экране, расположенном перпендикулярно к отраженному свету.

Решение:

Т.к. угол , будем считать клин плоскопараллельной пластиной, и для двух соседних максимумов можно записать условие их возникновения:

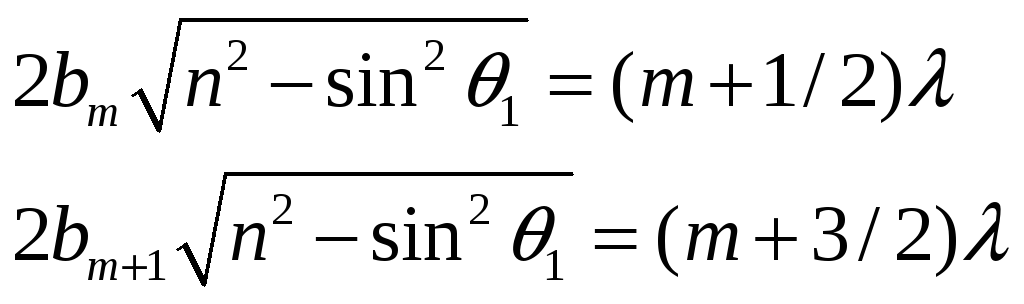
Вычтем из второго первое:

Заметим что это разность в толщине клина для двух падающих лучей. Т.к. мы считаем клин плоскопараллельной пластиной, можно считать, что , Тогда

Как видно из рисунка, . ■

№5.89

Свет с длиной волны мкм от удаленного точечного источника падает нормально на поверхность стеклянного клина. В отраженном свете наблюдают систему интерференционных полос, расстояние между соседними максимумами которых на поверхности клина мм. Найти:

а) угол между гранями клина;

б) степень монохроматичности света , если исчезновение интерференционных полос наблюдается на расстоянии см от вершины клина.

Решение:

а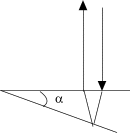) Воспользуемся результатом из предыдущей задачи. Записав условие максимумов для соседних максимумов и вычитая из второго уравнения первое, получим:

,

где =0, т.к. лучи падают на поверхность клина нормально. А . Получаем:

. ■

б) 1 способ:

Максимальный порядок интерференции можно найти, зная, что исчезновение полос начинается на расстоянии от вершины клина, и зная расстояние между соседними максимумами . В таком случае количество максимумов равно:

.

Нам также известно условие максимального порядка интерференции:

.

2 способ:

Из условия максимального порядка интерференции,

.

Максимальная оптическая разность хода, при которой еще наблюдается интерференция, она же – длина когерентности – равна:

.

С другой стороны, максимальная оптическая разность хода равна:

. ■

№5.90

Плоско-выпуклая стеклянная линза выпуклой поверхностью соприкасается со стеклянной пластинкой. Радиус кривизны выпуклой поверхности линзы R, длина волны света . Найти ширину кольца Ньютона в зависимости от его радиуса r в области, где .

Решение:

И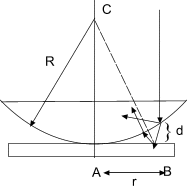з по теореме Пифагора: , из-за того, что расстояние между линзой и пластинкой очень мало можно пренебречь разницей между d и расстоянием, пройденным отраженным лучом от пластинки к линзе (которое по идее и должно стоять в теореме Пифагора), и можно ставить d- перпендикуляр от точки преломления луча из линзы и пластинкой в формулы. Получим 2Rd, так как можно пренебречь, 2-ой порядок малости. Тогда

.

2d - геометрическая разность хода (примерная) лучей, отраженных от пластинки и от выпуклой поверхности линзы. - оптическая разность хода,

,

Здесь мы еще прибавили полволны, так как происходит отражение от оптически более плотной среды. Итак,

Условие минимума:

,

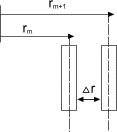
где - радиус темных колец. Для соседних колец имеем:

, .

,

здесь скобка , так как расстояния мало отличаются; (- ширина кольца Ньютона). Тогда

. ■

№5.91

Плоско-выпуклая стеклянная линза с радиусом кривизны R=40 см соприкасается выпуклой поверхностью со стеклянной пластинкой. При этом в отраженном свете радиус некоторого кольца r=2,5 мм. Наблюдая за данным кольцом, линзу осторожно отодвинули от пластинки на h=5,0 мкм. Каким стал радиус этого кольца?

Решение:

В начальный момент времени, аналогично предыдущей задаче, запишем теорему Пифагора:

(помним, что расстояние между линзой и пластинкой мало, поэтому возможно приближение к ; величинами 2-го порядка малости пренебрегаем):

Тогда геометрическая разность ходя выглядит следующим образом:

.

Из условия минимумов запишем выражение для оптической разности хода:

.

Здесь мы снова прибавляем полволны к 2, так как происходит отражение от оптически более плотной среды. Итак,

.

После передвижения опять записываем теорему Пифагора, только теперь расстояние, проходимое отраженным от пластины лучом, увеличивается на 2h.

,

(здесь опять используется приближение и пренебрежение очень малыми величинами).

Тогда геометрическая разность ходя выглядит следующим образом:

.

Оптическая разность хода:

.

Делая замену получаем:

. ■

№5.97

В двухлучевом интерферометре используется оранжевая линия ртути, состоящая из двух компонент =576,79 нм и =579,03 нм. При каком наименьшем порядке интерференции четкость интерференционной картины будет наихудшей?

Решение:

Четкость интерференционной картины будет наихудшей тогда, когда максимум от совпадет с минимумом от :

■

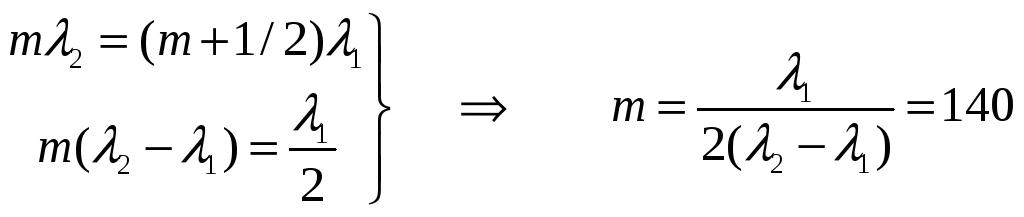№5.98

В интерферометре Майкельсона использовалась желтая линия натрия, состоящая из двух компонент с длинами волн =589,0 нм и =589,6 нм. При поступательном перемещении одного из зеркал интерференционная картина периодически исчезала (почему?). Найти перемещение зеркала между двумя последовательными появлениями наиболее четкой картины.

Решение:

Условие перехода от одной четкой картины к следующей: - условие максимумов, где m - некоторое целое число. Соответствующее перемещение зеркала определяется уравнением:

Умножаем на 2, так как луч проходит это расстояние дважды, и умножаем длину волны на целое число, так как нас интересуют максимумы.

.

Произведение , так как величины различаются очень незначительно. ■