Энергетический профиль ЭА |
|
||
Е |
X |
B |
|
A |
|
||
|
|
|
|
ЕХ |
|
|
|
АХ |
|
|
ВХ |
|
|
|
|
ЕА |
|
|
|
ЕВ |
ЕАВ |
|
|
|
|
|
|
Аи В — начальная и конечная химические формы
Х— переходное состояние (ПС) или активированный комплекс (АК)
ЕАВ — энергетический эффектАХ и ВХ — энергии активации
|
|
|
Константа равновесия |
|
|
|
NВ |
exp (– EВ |
/ kT ) |
K = —– = ——————— = exp (– Е / kT ) |
||||
|
|
NА |
exp (– EА |
/ kT ) |
|
|
|
Константы скорости |
|
kАВ |
~ |
exp (– АХ / kT ) |
Прямая реакция |
|
kВА |
~ |
exp (– ВХ / kT ) |
Обратная реакция |
|
kAB |
exp (– АХ / kT ) |
K = —— = ———————— = exp (– Е / kT ) |
|
kBA |
exp (– BХ / kT ) |
Стерический множитель (S) — доля траекторий, приводящих к вершине барьера
S = N / (N + N)
RHD |
А |
S << 1 |
|
||
|
|
|
|
N2 |
X |
В |
Скорость вылета |
газа |
||
|
RHH |
W ~ S/4 R2 |
0 |
|
|
|
|
Е |
|
АК |
|
+ Е |
– Е |
|
|
A
B
Трансмиссионный коэффициент (æ) — вероятность энергетической релаксации активированного комплекса
æ = 1 – 10–14
Теория абсолютных скоростей (ТАС)
Энергетический фактор |
РЕ |
|
Стерический фактор |
PS |
k ~ РЕ · PS · Pæ |
Релаксационный фактор |
Pæ |
|
Приближенные варианты
Цель: оценка высоты потенциального барьера, разделяющего исходную и конечую химические формы (энергии АК).
Два типа задач:
•сравнение реакционной способности серии реагентов в однотипной реакции,
•оценка селективностей превращения по нескольким альтернативным направлениям (каналам).
Принцип Белла-Эванса-Поляни (БЭП) |
|||
Молекула В – С реагирует с серией атомов Аi : |
|||
Аi |
+ В – С = Аi – В + С |
||
E |
|
B + C |
Кривая диссоциации |
|
связи В–С |
||
|
|
||
B–C |
εa |
[ Ai • • • B • • • C ] |
|
|
|||
Ai |
|
|
Энергетический |
|
|
|
профиль ЭА |
|
|
Ai –B |
Кривая образования |
|
|
|
|
|
|
|
связи Ai –B |
При постоянной верхней кривой, описывающей разрывающуюся связь, величина энергии активации будет тем меньше, чем ниже проходит вторая кривая, соответствующая образующейся связи.
Следовательно, чем больше суммарный выигрыш в энергии (энергетический эффект H ), тем меньше энергия активации.
Уравнение Эванса-Поляни
εа = а + b H
(позволяет оценить энергию активации через термодинамические характеристики реагентов)
Для газофазных реакций присоединения- элиминирования имеют место соотношения:
εа = 48 + 0,25 H |
(элиминирование) |
εа = 48 + 0,75 H |
(присоединение) |
Уравнение Сабо
εа = Di – Dj
где Di — энергии диссоциации разрушающихся связей, Dj — энергии диссоциации образующихся связей.
Метод молекулярной механики
|
dE1 |
dEn |
dE2 |
|
ds |
• 
•
• |
• |
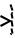• dE = min
dЕвал = (1/2) ( ki dri2 ) —
энергия валентных деформаций (растяжение химических связей);
dЕневал = (ae–br – c/r 6) –
– (ae–bro – c/ro6) —
энергия взаимодействия атомов, не связанных непосредственно химическими связями;
dЕ угл. = (1/2) ( fi d i2 ) —
энергия искажения валентных углов;
dЕторс = 1/2 k (1 + cos3 ) – 1/2 k (1 + cos3 o) —
энергия искажения невалентных углов;
dЕ = dЕвал + dЕневал + dЕугл + dЕторс + dЕспециф
Энергия активации для реакции замещения
R–Br + Br*– RBr* + Br–
R
H
CH3 i-Pr t-Bu
dЕ = dЕвал
эксперимент |
расчет |
0 |
0 |
7,1 |
7,5 |
16,3 |
15,0 |
25,1 |
23,0 |
+ dЕневал + dЕугл + dЕторс + dЕспециф
Вклад |
|
> 90 % |
( P 2 ) = min |
|
i |
|
CH= CH– CH3 |
|
( P 2 ) = 0,716 |
СН |
i |
|
|
Θ СН |
CH2 – CH= CH2 |
СН2 |
|
Na+ |
( Pi2 ) = 0,698 |
|