Классический предел по массе
Плотность уровней Ω ~ m
E 
В случае макроскопических частиц расстояния между уровнями становятся настолько малыми, что обнаружить их оказывается невозможно.
Вместо совокупности дискретных уровней образуется сплошная энегетическая зона.
m →
8
Влияние размера ящика |
E |
2 2 |
2 |
= ——– n |
|
||
E |
|
2mL2 |
|
E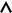 
n = 3
E
n = 3
n = 3
n = 2
|
n = |
2 |
|
|
|
|
|
|
|
n = 2 |
|
n = 1 |
n |
= |
1 |
n |
= 1 |
|
|||||
|
|
|
|
||
Молекула Н2 |
Молекула Н2 |
Молекула Н2 |
Классический предел по размеру
Плотность уровней Ω ~ L2
E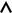 
В случае макроскопических размеров ящика расстояния между уровнями становятся настолько малыми, что обнаружить их оказывается невозможно.
Вместо совокупности дискретных уровней образуется сплошная энегетическая зона.
L →
8
Влияние размера ящика
Атом: L ≈ 10–10 м
E1 |
2 2 |
|
9,9 10–68 |
10 |
–17 |
Дж |
= ——– = ———————— ≈ 0,5 |
|
|||||
|
2mL2 |
2 |
9 10–31 10–20 |
|
|
|
Атомное ядро: L ≈ 10–15 м
E1 |
2 2 |
|
9,9 10–68 |
10 |
–7 |
Дж |
= ——– = ———————— ≈ 0,5 |
|
|||||
|
2mL2 |
2 |
9 10–31 10–30 |
|
|
|
Электрон не может длительное время (более чем 10–8 с) находиться внутри ядра
Давление и работа |
F |
2 2 |
2 |
|
= – ——– n |
|
|
E |
|
mL3 |
|
E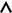 
W = ∫ F ∙ dL = – E
E
Работа над системой |
Работа над средой |
Два способа изменения энергии
4 |
4 |
2
3 |
3 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
2 |
|
|
|
|
1 |
1 |
работа 
теплота
Непрерывность Дискретность
Квантовое состояние |
Квантовое состояние |
сохраняется |
скачкообразно изменяется |
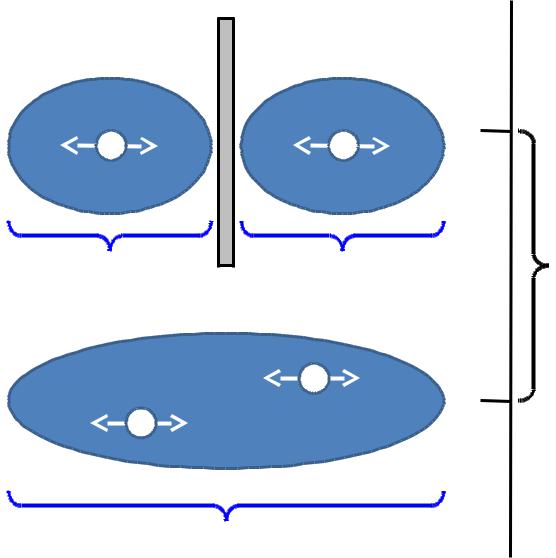
Природа химических связей
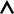Е
Два атома Н + Н
L |
L |
ΔЕ |
Молекула
Н—Н
≈ 2L
Влияние формы ящика
Расходящаяся |
Эквидистантная |
Сходящаяся |
система уровней |
система уровней |
система уровней |
Трехмерный ящик |
P = PX |
+ PY |
+ PZ |
Z |
nX |
nY |
nZ |
|
Z
L
L X
E = EX + EY + EZ
P
|
nX |
= 1, 2, 3, … |
|
Y |
nY |
= |
1, 2, 3, … |
|
nZ |
= |
1, 2, 3, … |
LY
X
= (x, y, z) = (x) (y) (z)
(nX, nY, nZ) |
n |
n |
Y |
n |
Z |
|
X |
|
|
Трехмерный ящик
P = |
nx |
ny |
nz |
| P | = 2mE |
— i |
+ — j + — k |
|||
|
Lx |
Ly |
Lz |
|
Е = Ex + Ey + Ez |
2 2 |
nx2 |
ny2 |
nz2 |
= —— —– + —– + —– |
||||
|
2m |
Lx2 |
Ly2 |
Lz2 |
(x, y, z) = (x) (y) (z) =
8 |
nx |
ny |
nz |
= — sin —— x sin —— y sin —— z |
|||
V |
Lx |
Ly |
Lz |
( V = Lx Ly Lz — объем ящика )
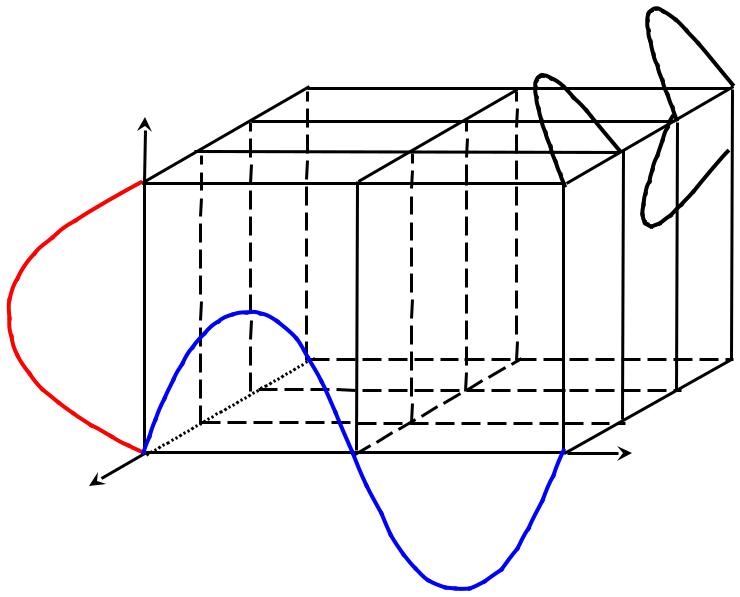
nX = 3 |
nY = 2 |
nZ = 1 |
|
|
+ |
z |
|
+ |
|
|
|
|
|
– |
+ |
|
|
|
+ |
|
x |
|
y |
|
– |