Общая методика решения КМ-задач
ЗАДАЧА: найти все возможные состояния объекта (векторы состояния или волновые функции Ф1, Ф2, …, Фn)
Уравнение
Шредингера
dФ(x, t)
–i ———— = H Ф(x, t) dt
Ф(x, t) = D1 1 + D2 2 + . . . + Dr r
волновые функции стационарных состояний (базисный набор)
Стационарный базис
Ф(x, t) = D1 1 + D2 2 + . . . + Dr r
1.Существует простой способ нахождения, так как функции стационарных состояний являются собственными для оператора Гамильтона:
Н (x) = Е (x)
2.Только стационарные состояния являются долгоживущими, поэтому все объекты, участвующие в медленных химических процессах (атомы, ионы, молекулы), заведомо находятся в стационарных состояниях.
3.Стационарные состояния удобно изучать экспериментально (большинство приборов действуют относительно медленно). При этом обеспечивается большая точность и надежность измерений.
Стандартный объект — «частица» (т.е. внутреннее строение объекта не учитывается), которая движтся как единое целое.
Характер движения зависит от внешних условий.
Потенциальная яма 
U = f(x)
Циклическое
движение
Х
Циклически движутся электроны в атомах и молекулах
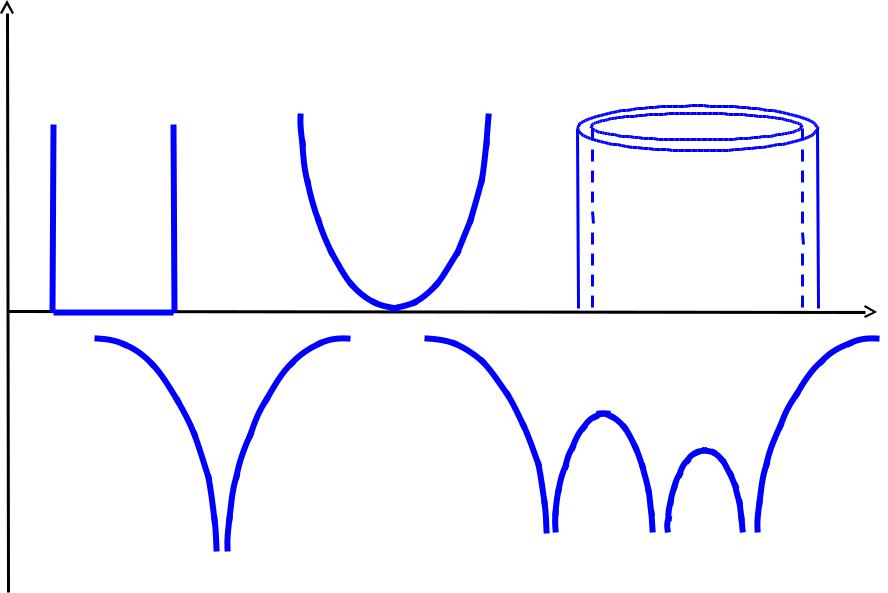
U = f(x) |
Разновидности ПЯ |
|
Ящик |
Осциллятор |
Ротатор |
Х
Атом |
Молекула |
Частица в «потенциальном ящике» (прямоугольной потенциальной яме)
U =8 |
U = 0 U =8 |
0 |
L |
X |
|
Возвратно-поступательное движение
Классическое описание
•ИМПУЛЬС, направленный вдоль оси Х, который может иметь
всего два возможных значения РХ = ± | Р |.
•ЭНЕРГИЯ Е = Т = Р 2/ 2m, имеющая определенное и постоянное значение, и всегда представляющей собой кинетическую энергию (за исключением точек возврата)
•ЧАСТОТА = | Р | / 2mL, имеющая смысл только для достаточно длинных промежутков времени.
P 
Вероятностная
функция
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
L |
||||
Адиабатический инвариант
Регулярные удары частицы о стенки ящика создают силу давления, уравновешиваемую внешними силами.
Если стенку ящика медленно перемещать, то эти силы будут совершать работу: над частицей (при уменьшении размера) или над окружающей средой (при увеличении размера).
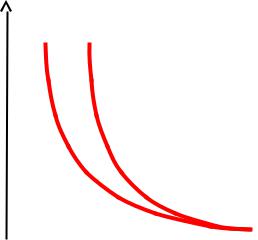
В итоге кинетическая энергия частицы и ее импульс будут зкономерно связаны с размером ящика:
T = f (L) |
Р = f (L) |
P T
Условие адиабатичности:
скорость перемещения стенки должна быть малой по сравнению со скоростью движения частицы
Vстенки << Vчастицы
L
Адиабатический инвариант |
Ai = Р L = const |
Р = Ai / L |
Т = Ai2 / 2mL2 |
Чем меньше размер ящика, тем больше импульс и кинетическая энергия (и наоборот)
Если уменьшить размер ящика в два раза, то импульс и скорость увеличаться вдвое, а энергия — вчетверо.
Частота ( = Р/2mL ) также возрастет вчетверо (увеличение
скорости в 2 раза и уменьшение длины пути в цикле в 2 раза).
|
Т = Ai |
|
|
|
E = h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
классическая механика |
квантовая механика |
||||||
Квантовомеханическое описание
Задача: найти все возможные состояния (способы движения) частицы в ящике;
для каждого состояния установить вид волновой функции и допустимые значения наблюдаемых:
φ(x, t) = ? E = ? P = ?
(x, t) = D1 1 + D2 2 + . . . + Dr r
Стационарные волновые функции
(собственные функции оператора Гамильтона)
E |
|
i — t |
= (x) еi t |
(x, t) = (x) е |
2 |
d 2 (x) |
– —— ———– = Е (x) |
|
2m |
dx2 |
(х) = А е ikx + В e–ikx
Уравнение на собственные значения для Н
Общее решение
В |
Любая точка окружности |
|
|
|
А2 + В2 = 1 |
А |
изображает возможное |
|
решение (при постоянном |
|
значении Е) |