3. Двойственные полиномы

P*(x) – полином двойственный P(x)

P*(x)=x^mP(1/x), где m – степень P(x).

Пример:

P(x)=x⁴+x+1

P*(x)=x⁴P(1/x)=x⁴(1/x⁴+1/x+1)=x⁴+x³+1.

Свойства двойственности:

а) Полином двойственный неприводимому полиному является также неприводимым;

б) Полином двойственный примитивному является также примитивным. P(x)= x⁴+x³+1.

Восьмеричное представление двоичных многочленов

Для удобства и компактности записи двоичные многочлены представлены в восьмеричном виде:x⁸+x+1  100 000 011  403

4 0 3

726  111 010 110  x⁸+x⁷+x⁶+x⁴+x²+x+1

Используя представление двоичных кодов в виде полиномов, дадим следующее определение циклического кода.

Циклический код образуется путем умножения информационного k-значного кода, выраженного в виде полинома Q(x) степени k-1, на некоторый образующий полином G(x) степени (n-k = r).

Q(x)=1010(x³+x); G(x)=(x³+x+1); E(x)=(x⁶+x³+x²+x).

1. Отсюда, основное свойство циклического кода: многочлен E, выражающий разрешенную кодовую комбинацию циклического кода, будет делиться на образующий многочлен без остатка.

2. С другой стороны: ни один многочлен, соответствующий запрещенной кодовой комбинации, на образующий многочлен G(x) без остатка не делится. То есть остаток – это проверочный синдром.

Это основное свойство позволяет определить наличие ошибки в кодовой комбинации.

Отсюда следующее:

1. Процедура кодирования состоит в умножении кодовой комбинации из информационных символов на образующий многочлен G(x).

2. Процедура декодирования состоит в делении принятой кодовой комбинации, выраженной в E(x) на образующий полином G(x) и определения остатка R(x).

Если R(x)=0 – нет ошибки,

Если R(x)0 – есть ошибка, и ее надо определить по виду R(x).

Требования к образующему g(X).

Корректирующие свойства циклического кода определяются в основном образующим полиномом G(x). Поэтому, выбор образующего полинома – важнейший этап построения циклического кода.

Процедура кодирования (получения кодовой комбинации без остатка делящейся на G(x)) может быть реализована тремя путями:

1. E₁(x)= Q(x)*G(x)

Исходная 

кодовая комбинация

Достоинство: простота

Недостаток: информационные и проверочные разряды перемешались, что усложняет процесс дешифрирования.

2. E₂(x)= Q(x)*x^n-k+ R(x), где R(x)- частное от деления Q(x)*x^n-k/ G(x)

Можно показать, что

F₂(x) делится без остатка на G(x)

Q(x) R(x)

Структурная схема

k r

Достоинство: полезная информация Q(x) отделена от проверочной R(x).

Требования к образующему полиному.

1) Для того, чтобы разрешенная кодовая комбинация при циклическом сдвиге влево (т.е. при «x» наx) оставалась разрешенной, т.е. делилась без остатка наG(x) необходимо, чтобыG(x) являлся сомножителемxⁿ-1.

Цикл. сдвиг



F₁(x)- разрешенная кодовая комбинация; E₂=E₁=E₁*x-C(xⁿ-1),

где C=0, если степеньE₁*x  n;

C=1, если степень E₁*x > n.

Отсюда, G(x) является сомножителем двучлена (xⁿ-1).

2) Из определения циклического кода – степеньG(x)= r = n-k

3) Циклический код принадлежит к линейным кодам. Циклический код, являясь линейным, способен различать и исправлять количество ошибок равное количеству различных комбинаций проверочного синдрома.

По аналогии: корректирующая способность циклического кода будет тем выше, чем больше остатков может быть образовано при делении многочленов (запрещенных с одиночными ошибками, или, что то же самое, различных векторов ошибок) на образующий полиномG(x).

Наибольшее количество остатков, равное 2^r-1 (т.е. равное n  2^r>n, т.е. числу векторов одиночных ошибок) может обеспечить только примитивный многочлен.

G(x) должен быть примитивным полиномом (специальные таблицы), т.е. являясь делителем двучленаxⁿ-1, не входит в разложениеx^+1,гдеn  представление в «свернутой» форме.

Пояснение: выбрать образующий полином кода (15,11)

(x¹⁵+1)

(x+1)(x²+x+1)(x⁴+x+1)(x⁴+x³+1)(x⁴+x³+x²+x+1)

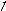
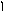
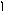
<3 =3 3

степень4 степень = 4

(x⁴+x+1) и (x⁴+x³+1) – можно выбрать в качестве G(x).

!!! Циклические коды, образованные с помощью двойственных многочленов – эквивалентные.

(x⁴+x³+x²+x+1) – нельзя выбрать какG(x), потому что:

1. формально, он входит x⁵+1515

2. фактически, дает не 2^r-1 (15 остатков), а только 5 остатков.

Операции кодирования – построение циклического кода с помощью образующей матрицы.

1. Для исключения (каждый раз) операция деления на практике построения циклического кода осуществляется при помощи образующей матрицы G_n,k(аналогично групповым кодам).

1

. Набор остатков от деления строже

. единичной матрицы, сдвинутой влево на

. Rij r разрядов, на P(x). При этом, вес каждого

1 остатка _Ri  d_min-1, что гарантировано

1 условием выбораP(x).

1

1

единичная, но

транспонированная матрица

Пример (*) _r

Выбрать образующий многочлен для случая n= 15 , m= 4. Двучлен x¹⁵+1 = x^{2 -1} +1 можно записать в виде произведения всех неприводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1,2,4.

В таблице неприводимых многочленов находим,

1 многочлен первой степени x+1

1 многочлен второй степени x²+x+1

3 многочлена четвертой степени x⁴+x+1, x⁴+x³+1, x⁴+x³+x²+x+1

x¹⁵+1 = (x+1) *(x²+x+1) *(x⁴+x+1) *(x⁴+x³+1) *(x⁴+x³+x²+x+1)

Один из сомножителей (x⁴+x+1), (x⁴+x³+1) может быть взят за образующий многочлен.

2. После построения образующей матрицы процедура определения проверочных разрядов аналогична этой процедуре линейных групповых кодов:

k

b_j = p_ij a_j , i = 1,2,3, …r

i=1