Лекции / Линейные коды

Лекция № .

Линейные коды.

Самый большой класс разделимых блочных кодов составляют систематические или линейные коды.

k r

a1

a2

a3

ai

…

ak

b1

b2

bi

br

n

Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.

Для двоичных кодов в качестве линейной операции используются сложение по mod 2.

b_j = a_i

(основаны на применении мат. аппарата алгебры Жегалкина (

Основное свойство линейного кода: сумма(разность) кодовых комбинаций является также разрешённой кодовой комбинацией.

Пример: [ ] - разрешённая



[ ] - разрешённая

=

[ ] - разрешённая

Отсюда – сумма(разность) произвольного числа разрешённых кодовых комбинаций является разрешённой кодовой комбинацией.

Линейные коды образуют алгебраическую группу по отношению к операции сложения по mod 2. В этом смысле они являются групповыми кодами.

Свойство группового кода: (d_min) Минимальное кодовое расстояние между векторами линейного кода равно линейному весу ненулевых кодовых векторов.

Для построения групповых кодов (т.е. перехода от информационных разрядов к полному кодовому слову, включающему также и проверочные разряды, целесообразно использовать специальные матрицы: n _* k = (k + r) _* k/

Порождающая матрица может быть представлена в виде 2^х матриц И(информационной) и П(проверочной) ||G|| = |[И]| |[П]|

a₁₁ a₁₂ … a_1k p₁₁ p₁₂ … p_1r

G_n,k = a₂₁ a₂₂ … a_2k p₂₁ p₂₂ … p_2r k

k ……………… ………………..

a_k1 a_k2 … a_kk p_k1 p_k2 … p_kr

k r

n

Получение кодовой комбинации осуществляется путём суммирования элементов ||И|| и параллельного суммирования строк ||П||.

1). На практике установлено, что в качестве информационной матрицы ||И|| удобно брать единичную матрицу в канонической форме:

100…0

I_и = 010…0

………

000…1

2). Строчки образуют матрицы ||C|| = ||И|| ||П|| представляют собой “К” комбинаций(разрешённых) искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы.

Пример

a₁ 1 1000 111 011 Необходимо закодировать

a₂ 0 0100 110 101 информационную комбинацию:

a₃ 1 0010 101 110 1011

a₄ 1 0001 011 111

Полученное значение проверочных

1011 001 разрядов.

В общем случае: a₁, a₂, a₃, a₄ – информационная кодовая комбинация в общем виде:

a₁ a₂ a₃ a₄ b₁ b₂ b₃ b₁ = a₁ a₂  a₃ Для заданной образующей матрицы

b₂ = a₁ a₂  a₄

b₃ = a₁ a₃  a₄

В самом общем случае алгоритм образования проверочных символов b₁…b₂ по известной информационной части a₁, a₂, … a_k может быть записан следующем образом :

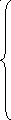_k

b₁ = p₁₁a₁  p₂₁a₂  …  p_k1a_k = p_i1a_i

ⁱ⁼¹

_k

b₂ = p₁₂a₁  p₂₂a₂  …  p_k2a_k = p_i2a_i

ⁱ⁼¹

----------------------------------------------

_k

bj = p_1ja₁  p_2ja₂  …  p_kja_k = p_ija_i

ⁱ⁼¹

----------------------------------------------

_k

b_r = p_1ra₁  p_2ra₂  …  p_kra_k = p_ira_i

ⁱ

Рассмотрим теперь метод построения образующей матрицы

Из свойств группового следует, что

W  d_min

С другой стороны W_i = Wн_i + Wпi  d_min

W_п  d_min – Wн

Т.к. вес всех сторон ||Н|| : W₁₁=1, то имеем

Wп  d_min – 1, d_min  t+1 d_min –1  t

Wп  d_min – 1  t  Wп  t

Необходимые и Отсюда: для кодов, обнаруживающих t – кратные ошибки:

достаточные требования W_{п (строки)}  t

для построения проверочной для кодов, исправляющих t – кратные ошибки :

матрицы W_{п (строки)}  2t

Рассмотрим частные случаи:

1.) Коды, обнаруживающие одиночную ошибку.

d_min = 2 ( N=15, t=1 )

W_п  1

Единая матрица для d_min  2

100…0 1 _{k k}

010…0 1 b₁ = a_ip_1i = a_i Не что иное, как

001…0 1 ^{i=1 i=1} проверка на четность.

000…1 1

И П

Во всех комбинациях построенного кода – четное.

Для d_min  3 проверочная матрица не может быть представлена в общей (единой) форме, т.к. для d_min  3  r зависит от k.

Построение кодовой комбинации E в матричной форме имеет вид:

образующая матрица

E = IG_n,k , где I – вектор длины k, компонентами которой являются

информационные разряды.

кодовый вектор информационный

вектор

Пример

Построить образующую матрицу и кодовую комбинацию для линейного кода, исправляющие одиночные ошибки при передаче собщений.

1. t = 1; N = 16;

2. d_min = 3; W_п = 2; k = [ log15] = 4; 2^r > k + r  r = 3;

3. G_п,к = G_7,4 =

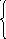a₁ ..a₄ b₁.b₃

1000 011 b₁ = a₂  a₃  a₄

0100 101 b₂ = a₁  a₃  a₄

0010 110 b₃ = a₁  a₂  a₄

1. 111

4. E = IG_п,к = 0 100.101

Рассмотрим этап депозирования  S₁, S₂ … S_r;

а.) В процессе депозирования осуществляются проверки, идея которых в общем случае может быть представлена следующем образом :

_k

S_j = b_j  p_ija_i  S_j = b_j  b_j’; j1r;

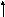
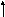
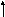
ⁱ⁼¹

новый старый из канала до передачи

проверочные символы

б.) S_j – называется проверочным синдромом или синдромом ошибок и имеет число разрядов равное: r ( S₁­, S₂ …S_r )

Если w(S_j’) = 0, но нет ошибок;

w(S_j)  0, есть ошибки.

в.) Рассмотрим процедуру исправления ошибки по виду S_j (из предыдущего примера

E = 0101.101)

Групповой код построен по матрице

1000.011

0100.101 = G_7,4

0010.110

0001.111

Покажем процесс исправления ошибки в произвольном разряде корректирующего кода.

1. Согласно правилу построения проверочного синдрома

S₁’ = (b₁,a₂,a₃,a₄)

S₂ = (b₂,a_1,a₃,a₄)

S₃ = (b_3,a_1,a_2,a₄)

Определим соответствие между ошибкой в определенном разряде принятой комбинации и видом проверочного синдрома. (Напоминаю, что для удобства полученную кодовую комбинацию будем рассматривать как суперпозицию (данном случае, как сумму по mod2) правильной (разрешенной, передаваемой) кодовой комбинации A и вектора одиночной ошибки _e).

2. Пусть информация принята верно, т.е. ни один из разрядов a_i, b_j не исказился. В этом случае b₁= a₂  a₃  a₄ сохранится равенство для всех трех строчек, а следовательно S_i = 0. Это подтверждает необходимый и достаточный признак принятия правильной информации.

3. Строем проверочную матрицу H, для которой строки – возможные вектора ошибок, а столбцы – проверочные синдромы соответствующие данной ошибке.

e₁ S₁

e₂ S₂

. .

. .

. .

e_n S_n

1 0 0 0 0 0 0 0 1 1 Корректирующая матрица H:

ошибка 0 1 0 0 0 0 0 1 0 1 i^ая строка корректирующей

в информационном 0 0 1 0 0 0 0 1 1 0 матрицы H содержит синдром,

разряде 0 0 0 1 0 0 0 1 1 1 = H который соответствует ошибке

в i-ом разряде кодовой

ошибка 0 0 0 0 1 0 0 1 0 0 комбинации.

в проверочном 0 0 0 0 0 1 0 0 1 0

разряде 0 0 0 0 0 0 1 0 0 1

a₁a₂a₃a₄ b₁b₂b₃ S₁S₂S₃

Для e₁ из выражений для S_i находим S₁, S₂, S₃.

Подчеркнуть, что S_i=0, если ошибочная комбинация не попадает в систему проверки для S_i.

Мы видим, что проверочная матрица H состоит из двух частиц матрицы П и единичной матрицы.

Данная методика построения проверочной матрицы является обобщающей (одинаковой для всех образующих матриц).

Т.о. процесс декодирования кодовых комбинаций (для линейного группового кода) состоит в следующем:

1. Определение проверочного синдрома S_i в соответствии с видом проверочной матрицы П.

2. Если S_i = 0 – комбинация принята верно, если S_i0, произошла ошибка.

3. Построение проверочной матрицы, которая устанавливает соответствие между значением S_i и позиций, в которой произошла ошибка.

4. Исправление (коррекция [инверсия]) ошибочной позиции.

Мы рассмотрели групповые линейные коды и процедуры кодирования и декодирования, в основе которых лежит построение порождающей (S) и проверочных матриц (H).

Наряду с решением вопроса построения линейного кода с заданной корректирующей способностью, существенным является вопрос об избыточности и простоте структурной реализации. С этой точки зрения линейные коды разделяются на совершенные (плотно упакованные) и несовершенные линейные коды.

1. Совершенные коды – коды с min количеством избыточных разрядов. [2^r = k+r+1]

Пример для кодов, исправляющих одиночные разряды.

(l = 1)

2^r > k+r,

k(количество информац.) r(количество проверочн.)

3. 3

4. 3

5. 4 (7,4)

6. 4

7. 4 «совершенные» min избыточность: r/(k+2)

8. 4

9. 4

10. 4 (15,11)

11. 4

12. 5

13. 5

14. 5

15. 5

несовершенные коды

2. С точки зрения простой структурной реализации:

экономические коды коды с повышенной

с min количеством проверок на четность корректирующей способностью

При построении проверочной матрицы  П , условие W_п  2l.

W_п = min: 2l, 2l +1, 2l +2, … W_п = max: r, r-1, r-2 … Min количество проверок на четность, Наиболее высокие корректирующие

min количество аппаратурных затрат способности.

Представление операции декодирования в матричной форме.

а) ẼH = S – из условия построения проверочного синдрома.

б) ẼH = (E  e)H = EH  eH = S;

При отсутствие ошибок: Ẽ=E; S=0; отсюда EH=0; eH=S; т.к. E=G_n,k, то G_n,kH=0, и имеем G_n,kH=0, условие построение H по известной G_n,k.

Пример:

1. 1000 011 011

G_n,k­= G_7,4 = 0100 101 ; H = 101 ,

0010 110 111

0001 111 100

010

001

2. I = 1010 E=IG_7,4=1010.101;

e =0010.000;

Ẽ = 1000.101

3. S=ẼH = 110 011

1000011 101 000

GH = 0100101  110 = 000 = 0.

0010110 111 000

0001111 100 000

010

001

Важным вопросом на практике является структурная реализация кодирующих и декодирующих устройств.

Поэтому (для сравнения) рассмотрим коды, Хэмминга, обладающие аналогичной корректирующей способностью, но с точки зрения структурной реализации дающие несколько другие результаты.

Матричное представление кода Хэмминга.

а) а₄ а₃ а₂ а₁ b₃ b₂ b₁ a₄ a₃ a₂ b₃ a₁ b₂ b₁

1 0 0 0 1 1 1 1 0 0 1 0 1 1

0 1 0 0 1 1 0 G_7,4^x = 0 1 0 1 0 1 0

0 0 1 0 1 0 1 0 0 1 1 0 0 1

0 0 0 1 0 1 1 0 0 0 0 1 1 1

a₁ a₂ a₃ b₁ a₄ b₂ b₃

E = IG_7,4 = (0101) G_7,4^x = 0 1 0 1 1 0 1

a₁ a₂ a₃ b₁ a₄ b₂ b₃ S₁ S₂ S₃

1 0 0 0 0 0 0 1 1 1

0 1 0 0 0 0 0 1 1 0

0 0 1 0 0 0 0 1 0 1

0 0 0 1 0 0 0 1 0 0

0 0 0 0 1 0 0 0 1 1

0 0 0 0 0 1 0 0 1 0

0 0 0 0 0 0 1 0 0 1

б) Этап декодирования.

111 Из определения H, в которой каждая строка равна

100 синдрому ошибки.

101

S = ẼH = Ẽ 100

010

010

001

S = 0111.101H = 101.

Структурная реализация линейных кодов и Хэмминга.

а) Кодирование

б) Декодирование

Модифицированный код Хэмминга.

Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность.

_{3 4}

Тогда : b₄= b_i   a_{i ;} Код (8, 4)

^{i=1 i=1} a₄a₃a₂b₃a₁b₂b₁b₄

S=EH;

_{4 4}

S₁=  b_i   a_i

^{i=1 i=1}

S	S1
0	0	Нет ошибок
0	1	Одиночная ошибка
0	0	Двойная ошибка
?	1	Тройная ошибка

Заключение:

а) Рассмотрены групповые линейные коды

Дстоинства

б) Достаточно эффективны при малой кратности ошибок (как правило, t=1).

Недостатки

в) При ошибках большей кратности – резкое усложнение кодирующих и (особенно) декодирующих устройств.

г) Более совершенными являются циклические коды.