Аппаратное умножение двоичных многочленов

Выход

«1»

«0»

а₁

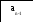
Вход

А(х)

C(x) = A(x)*B(x) = (a_nxⁿ + a_n-1x^n-1 + … + 1)(b_nxⁿ + b_n-1x^n-1 + … + 1) = b_na_nx²ⁿ + (a_nb_n-1 +a_n-1b_n)x^2n-1 + +…..

1^ый такт: на вход подается a_n, а на выходе получаем: a_nb_n.

2^ой такт: на вход подается a_n-1, а на выходе получаем: a_n-1b_n + a_nb_n-1 и т.д.

Пример:

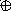
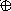
Выход

01001111

Вход

11001

A(x) = x⁴ + x + 1 C(x) = A(x)*B(x) =

А(х) B(x) = x³ + x² + x = x⁷+ x⁶+ x⁵+ x⁴+ x

Nтакта	Вход	a0 a1	Выход
0	11001	0 0	10 0
1 2	1100 110	0 0 1	11 111
3 4	101 1	0 0 1 0	1111 01111
5 6	0 0	1 0 1	001111 1001111
7 8	0	0 0	01001111

Аппаратное деление многочленов.

110000001

0

1

1

0

b₄=1

b₃=0

b₂=0

b₀=1

b₁=1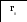

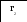
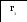
Выход

Вход

11001

Nтакта	Вход	r0 r1	r2 r3	Выход
0 1	110 000 001 11 000 000	0 0	0 0 0	0 0
2 3	1 100 000 110 000	1 0 0	0 1 0	0 0
4 5	000 1 100	0 1	1 0 0	0 1
6 7	110 11	1 0 0	1 0 1 1	01 001
8 9	1 0	1 0 1 оста	1 0 ток	1001 11001 частное

x⁸+x+1 x⁴+x+1 1) Делимое и делитель - нормированы

x⁸+x⁵+x⁴ x⁴+x+1 2) Степень делимого  степени делителя

x⁵+x⁴+x+1

x⁵+x²+x

x⁴+x²+1

x⁴+x +1

x²+x

2.Виды многочленов

а) неприводимый простой многочлен.

Многочлен P(x) степени n называется простым, если он не делится без остатка ни на какой многочлен степени меньшей, чем n (аналогия с простым числом).

n=4: x⁴+x+1; x⁴+x³+1

n=5: x⁵+1=(x+1)(x⁴+x³+x²+x+1)  составной (непростой)

n=10: x¹⁰+x³+1; x¹⁰+x⁷+1 и т.д.

б) примитивный многочлен.

Примитивным называется многочлен P(x) степени m, имеющий максимально возможное число остатков от деления xⁱ/P(x)- 2^m-1, где i = 0,1…..

Пример. P(x)=x⁴+x³+x²+x+1 – непримитивный

P(x)=x⁴+x+1 – примитивный

i	R(x) - остаток при xi/P1(x)	R(x) - остаток при xi/P2(x)
<0 1 2 3 4	<0001 0010 0100 R=1 1000 1111	0001 0010 0100 1000 0011
5 6 7 8	0001 0010 0100 1000 R>1	0110 1100 1011 0101
9 10 11 12	1111 0001 0010 0100	1010 0111 1110 1111
13 14 15 16	1000 1111 0001 0010	1101 1001 0001 0010
17 18 19 20	0100 1000 1111  0001	0100 1000 0011 0110