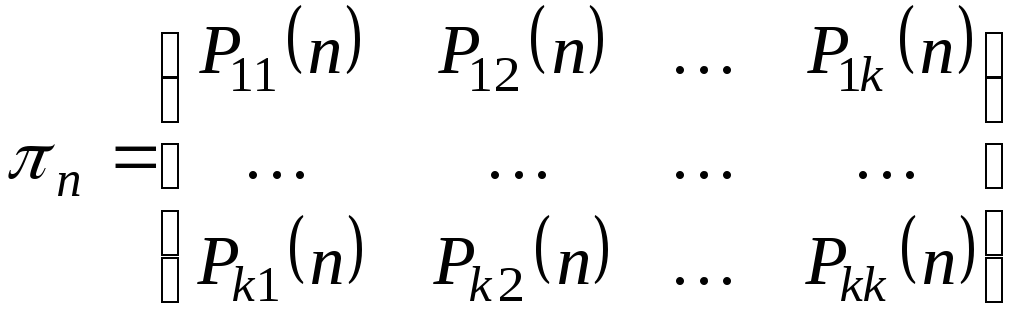Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / Шпора12
.doc|
57.
Критерий
Критерий
Процедура
применения критерия
Этапы:
Если
Х–СВНТ – разбить множество значений
на r
– непересекающихся интервалов
Х–СВНТ
вычислить
e – количество оцениваемых параметров. Малочисленные частоты надо будет объединять. Проверка гипотезы о равномерном распределении генеральной совокупности. n = 200 А;
1.
2.
k = 10 – 2 – 1 = 7
|
59. Переходные вероятности.
Матрица
перехода.
Далее будем рассматривать только
однородные цепи Маркова, в которых
условная вероятность появления
события
Назовем
эту вероятность – вероятностью
перехода и обозначим
Полную вероятностную картину возможных изменений, осуществляющихся при переходе от одного испытания к следующему можно задать с помощью матрицы
Замечание.
Опр. Любая квадратная матрица, элементы которой удовлетворяют следующим требованиям:
Одной из главных
задач в теории цепей Маркова является
задача определения вероятности
перехода
Рассмотрим
какое-нибудь промежуточное испытание
с номером (S+m).
В этом испытании осуществится
какое-либо одно из возможных событий
По формуле полной вероятности получим
Обозначим через
Согласно формуле
(*) получаем, что
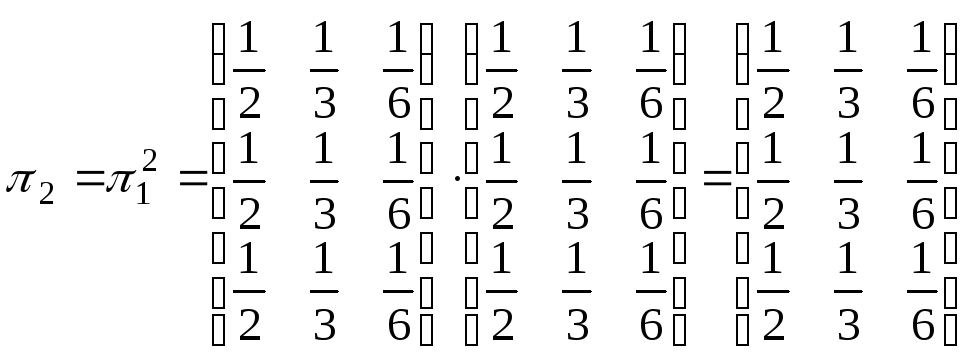
В частности, когда n = 2, получаем
n = 3
Отметим частный случай формулы (*), когда m = 1
Пример 2 Процесс блуждания с отражением.
Пусть частица,
находящаяся на прямой, движется по
этой прямой под влиянием случайных
толчков, происходящих в моменты
времени
Получается цепь Маркова с конечным числом состояний.
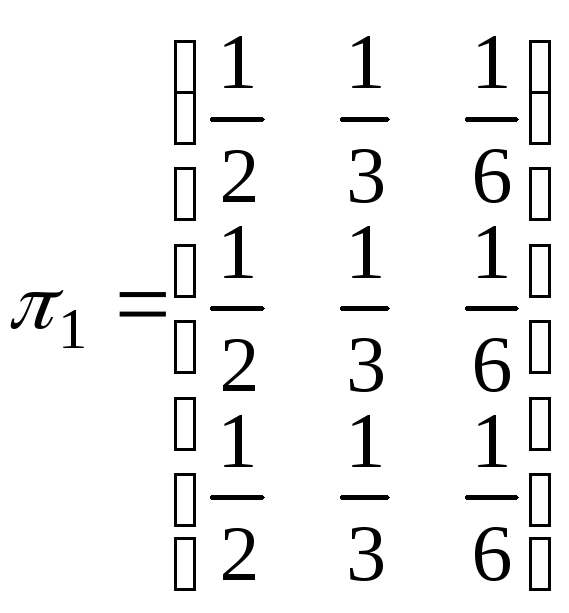
Аналогично можно рассматривать ситуации, когда частица прилипает к одной из стенок, этот процесс блуждания с поглощением. Лекция № 23 Пример 3. Вероятности перехода даются матрицей
Чему равно число состояний в системе? Ответ: 3. Найти вероятности перехода из состояния в состояние за два шага:
|
58. Марковская зависимость испытаний. Определение цепи Маркова.Непосредственным обобщением схемы независимых испытаний является схема цепей Маркова. Пусть производится последовательность испытаний, в каждом из которых может осуществляться одно и только одно из k несовместных событий.
верхние индексы обозначают номер испытания.
Опр.
Последовательность
испытаний образует простую цепь
Маркова, если условная вероятность
в
Замечание.
Часто при изложении теории цепей
Маркова придерживаются иной терминологии
и говорят о некоторой физической
системе S,
которая в каждый момент времени может
находиться в одном из состояний
Для
цепей Маркова вероятность перейти в
какое-либо состояние
Пример
1. В модели
Бора атома водорода, электрон может
находиться на одной из допустимых
орбит. Обозначим, через
Разность (i–j) зависит от количества энергии, на которую изменился заряд атома в момент времени tS. Это пример цепи Маркова с бесконечным числом состояний.
продолжение 26: Пример.
Время
безотказной работы ЭВМ – это СВ Т,
имеющая показательное распределение
с параметром l.
Физический смысл l
– это среднее число отказов в единицу
времени, если не учитывать простоев
ЭВМ. Известно, что ЭВМ уже проработало
без отказов время t.
Найти при этом условии плотность
распределения
Решение.
Так как простейший поток отказов не имеет последствия, то вероятность появления хотя бы одного отказа на участке (t, t + t) не зависит от того, появлялись ли отказы ранее момента t.
Найдем
Вывод: Таким образом распределение времени, оставшегося до следующего отказа, не зависит от того, сколько времени ЭВМ уже отработало без отказов.
|

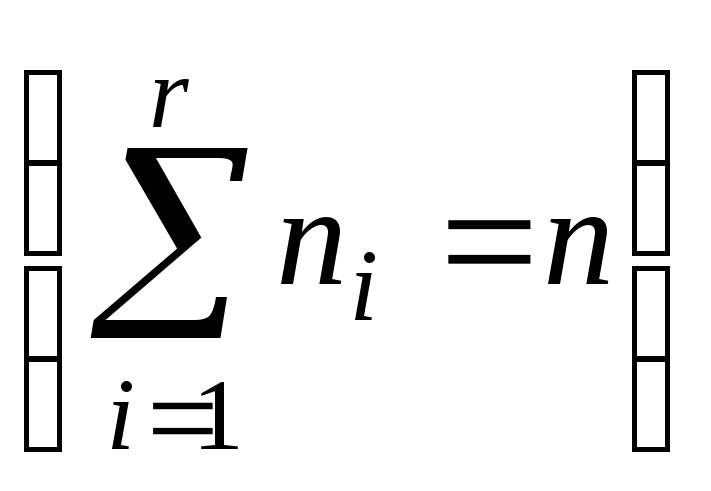 .
.
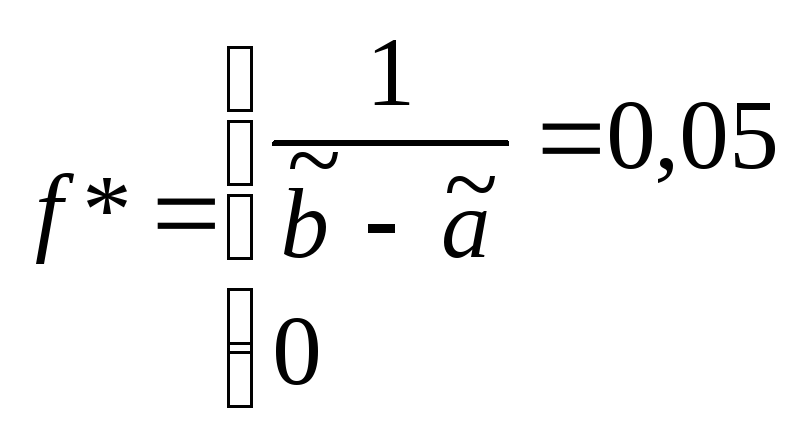
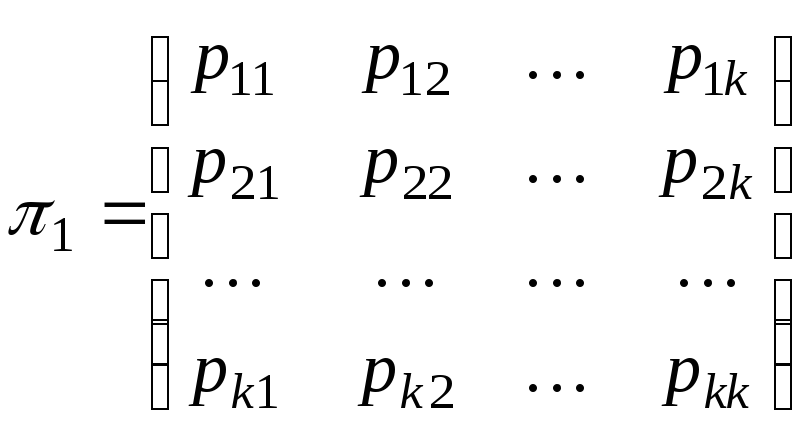 – матрица
перехода
– матрица
перехода