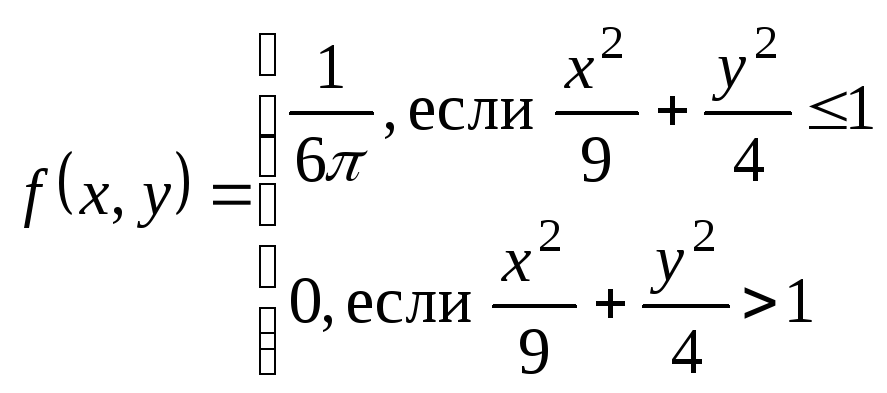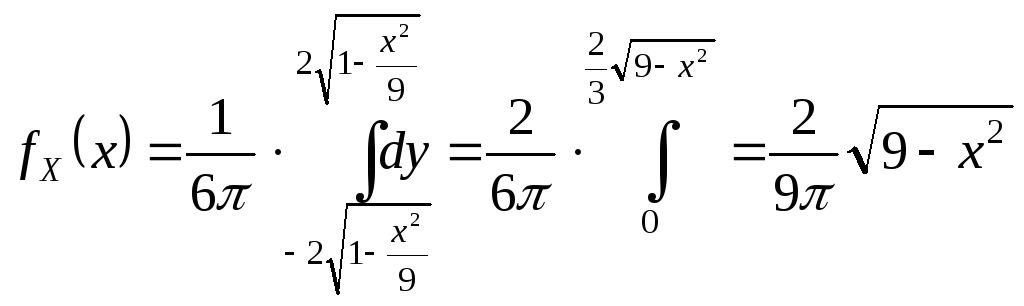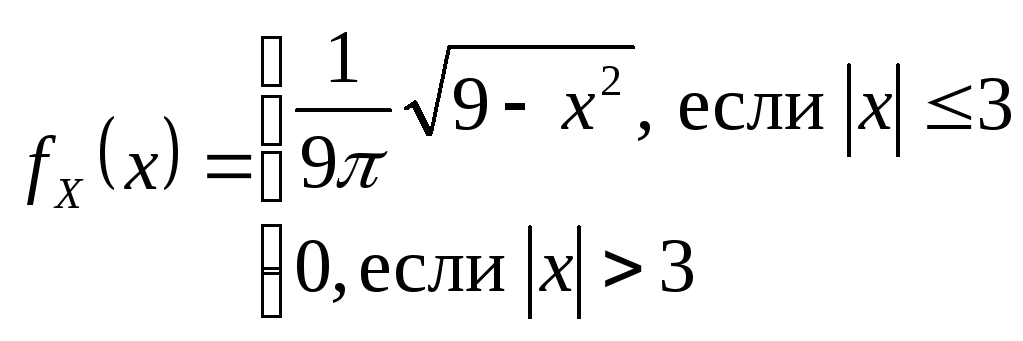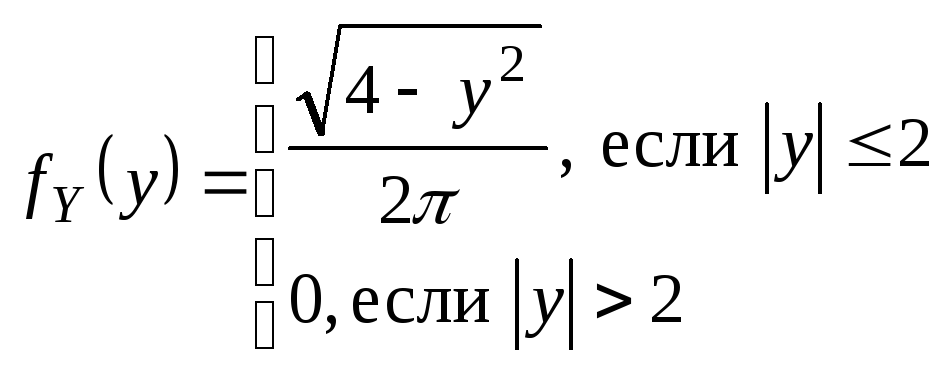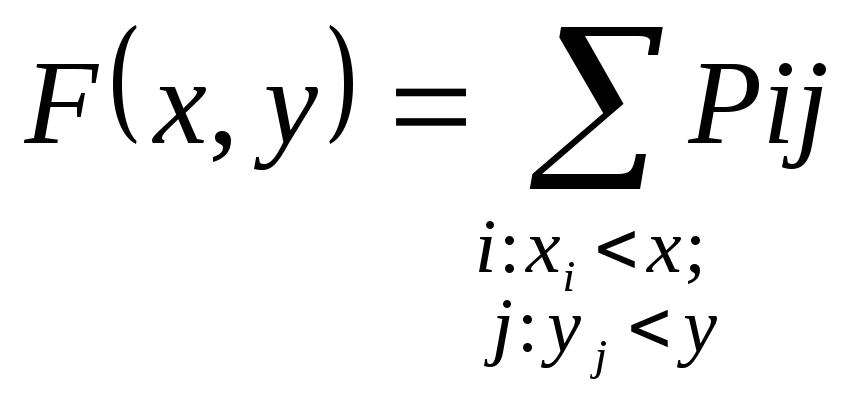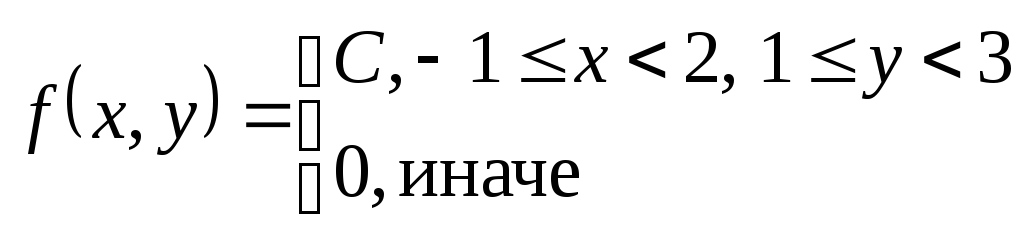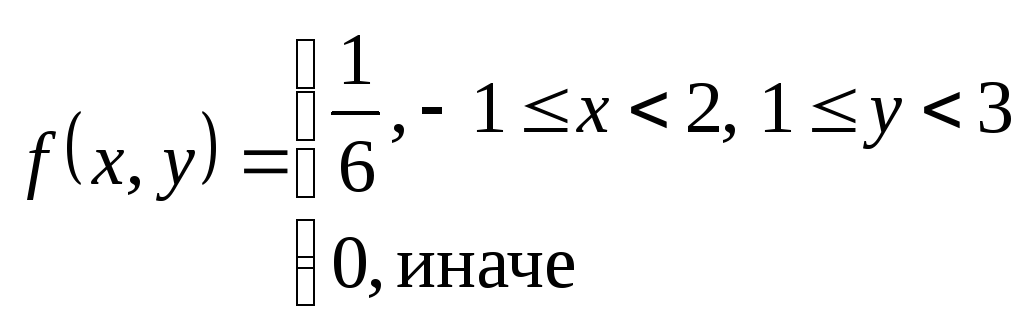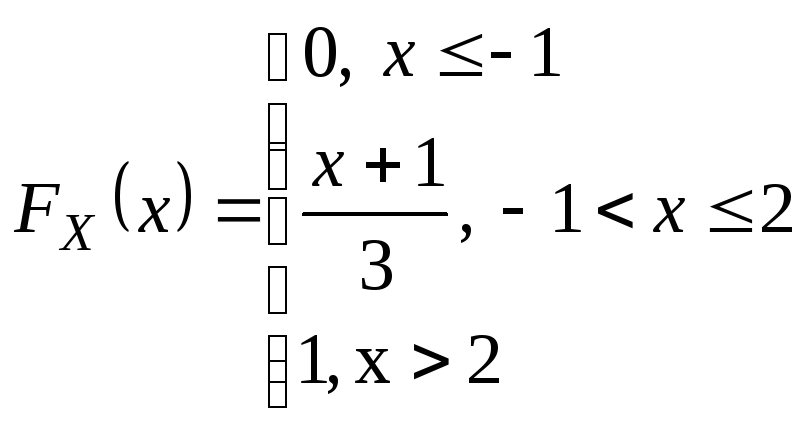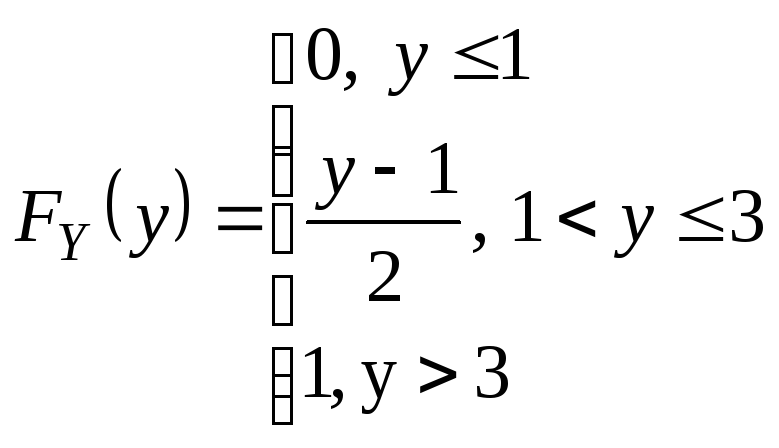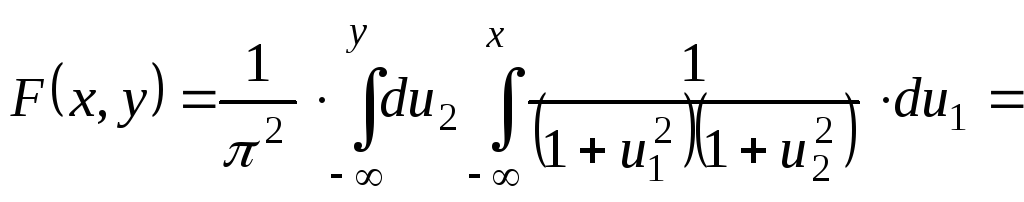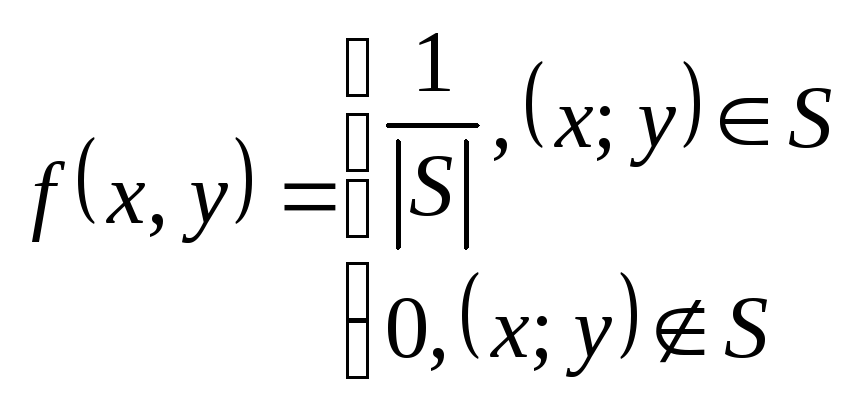Шпаргалки / Шпаргалки (Бардушкин) / Шпаргалки в Word / шпора6

29.Системы случайных величин (случайные векторы) Совместная функция распределения

Пусть на одном и том же вероятностном пространстве (,A, P) задано n СВ, , совокупность – называется многомерной (n-мерной) СВ или случайным вектором.

Совместная функция распределения

Рассмотрим в одном и том же вероятностном пространстве (,A,P) набор СВ . Так как множество , таких пересечения , поэтому существует вероятность этого события, которая называется многомерной функцией распределения.

Замечания:

1.В дальнейшем ограничимся случаем двух случайных величин .

2. Функция – вероятность того, что случайная точка попадает в бесконечный квадрант с вершиной в точке .

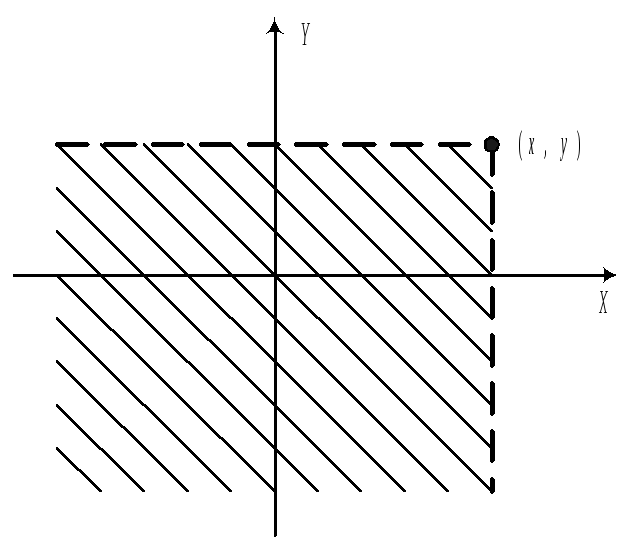
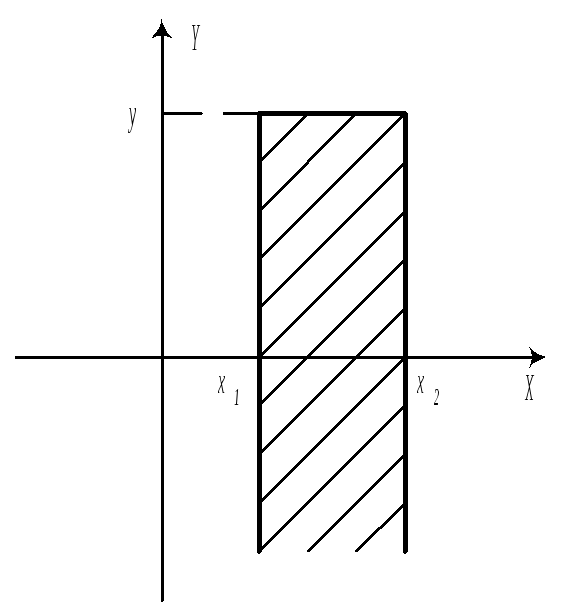
С помощью F, можно вычислить вероятность попадания случайной точки в полуполосу или в прямоугольник.

а)

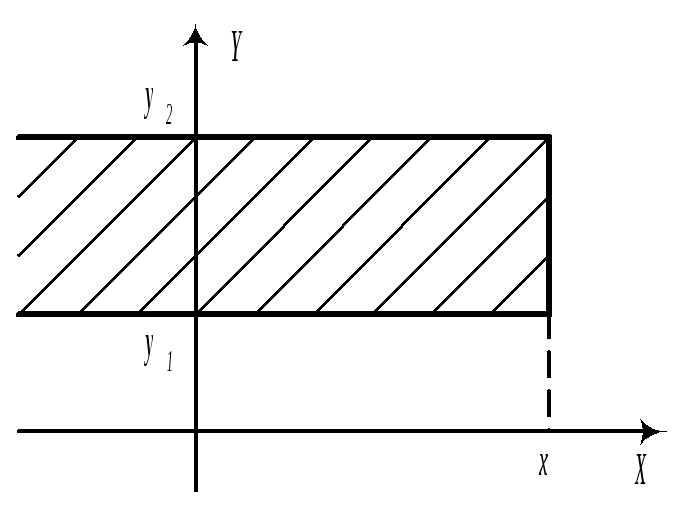
б)

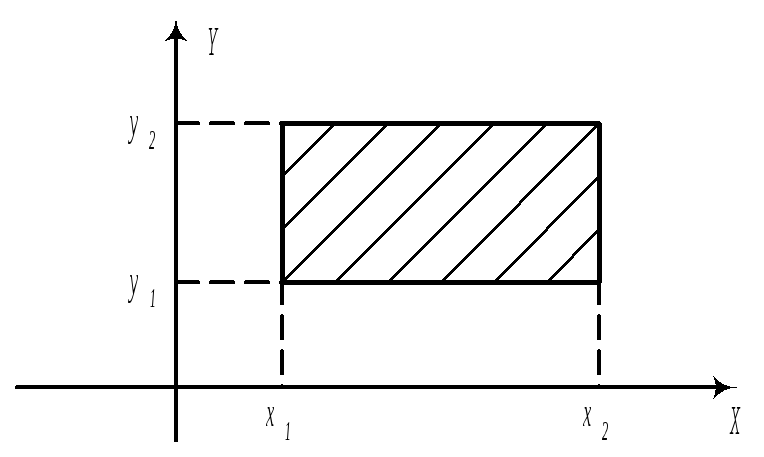
в)

Пример.

продолжение 31:

Пример.

Найти:

– ? – ?

Аналогично

30.Дискретные двумерные случайные величины

Опр. Двумерная СВ (X, Y) называется дискретной, если каждая из СВ и Х и Y является дискретной.

Пусть СВ Х может принимать значения , а СВ Y принимает дискретные значения .

Двумерный случайные вектор может принимать только пары значений

По этой таблице нетрудно определить функцию распределения.

.

Найти одномерные законы распределения компонент X и Y.

Найти вероятность того, что – ?

– ?

Решение.

32.Зависимые и независимые СВ,

В двух предыдущих параграфах было показано, как зная закон распределения системы двух (дискретных или непрерывных СВ) найти законы распределения отдельных компонент X и Y.

Вопрос. Можно ли, зная законы распределения отдельных СВ (X, Y) входящих в систему , найти закон распределения всей системы? Нет, в общем виде этого сделать нельзя – это можно сделать только в одном частном случае, когда СВ X и Y образующие эту систему—независимы.

Опр. Две СВ X и Y называются независимыми, если независимы все связанные с ними события

Замечание. Так как зависимость и независимость событий всегда взаимны, то зависимость и независимость СВ, также всегда взаимна: если X не зависит от Y, то Y не зависит от X.

В терминах законов распределения, независимость СВ можно определить так: две СВ называются независимыми, если закон распределения каждой из них не зависит от того какое значение приняла другая.

Если компоненты X и Y двумерного вектора (X, Y) независимы, то функция распределения выражается, через функции распределения отдельных компонент.

и – независимы.

Это правило является необходимым и достаточным условием независимости для любого типа СВ.

1. Если X и Y независимые дискретные СВ с матрицей распределения .

2. Непрерывные СВ.

Пример.

Найти:

С – ?, зависимы или независимы X и Y – ?

– ?

Решение:

выполняется =>независимы

Раз компоненты независимы, значит .

Если СВ образующие систему зависимы, то для нахождения закона распределения системы не достаточно знать законы распределения отдельных величин, входящих в систему, требуется знать так называемый условный закон распределения одной из них.

31.Непрерывные двумерные СВ

Пусть A – -алгебра множеств двумерного пространства R², порожденная всевозможными прямоугольниками вида

.

Опр.Двумерной плотностью распределения называется такая функция, что вероятность , где .

Из определения следуют ее свойства.

Свойства.

I. .

II. (условие нормировки).

III. .

IV. .

Опр. Двумерная СВ (X; Y) называется непрерывной, если ее распределение имеет .

Пример 1:

– ?

Решение.

.

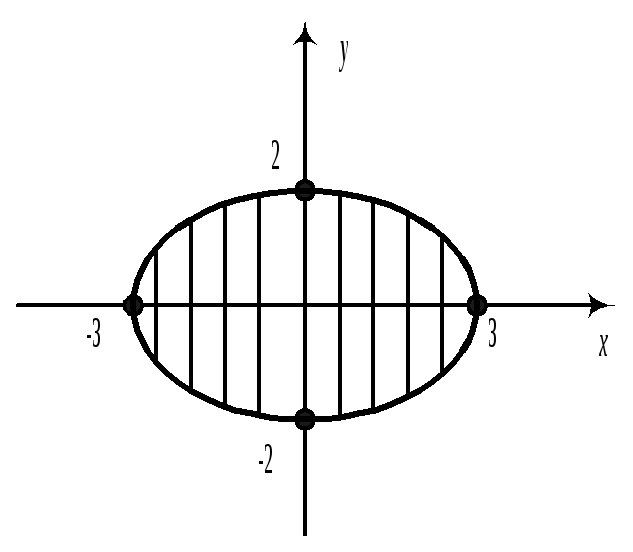
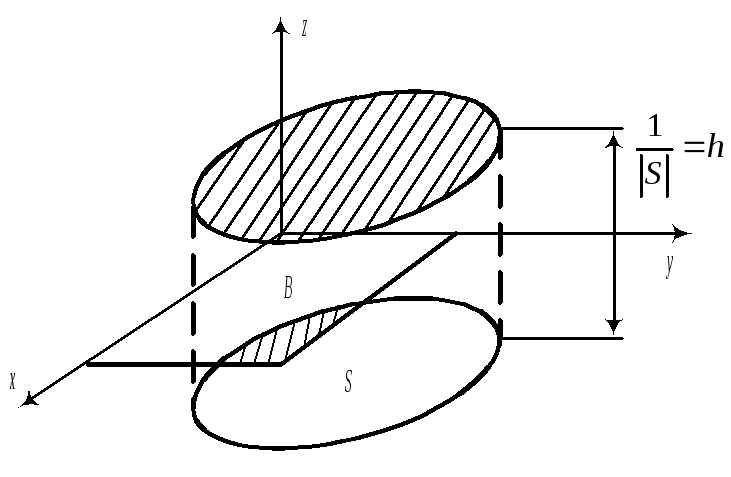
Пример 2:(двумерное равномерное распределение)

Плотность равномерного распределения на области конечной двумерной площади .

Замечание.

По последней формуле вычисляются так называемые геометрические вероятности.

Пусть известна . Найдем плотности распределения каждой из компонент X и Y.

Решение.

(*)

Продифференцируем обе части равенства (*) по Х, получим

продолжение 29:

Решение

Из формулы вероятности попадания в прямоугольник и определения многомерной функции распределения , вытекают следующие свойства, которые доказываются аналогично одномерному случаю.

Свойства.

1. по каждому аргументу не убывает и непрерывна слева.

2. .

3. .

4. а) При становится функцией распределения компоненты x.

.

б) При становится функцией распределения компоненты y.

.