Лекции / Лекции (ЭКТ-2, Бардушкин) / Лекции в Word (2003) / Лекция 16,17

КУРС ЛЕКЦИЙ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Лекция № 16

§ 7. Условные числовые характеристики системы СВ (X;Y). Регрессия.

Определение.

Условным математическим ожиданием одной из СВ входящих в систему (X; Y) называется ее МО вычисленное при условии, что другая СВ приняла определенное значение.

Замечание.

То есть МО найденное на основе условного закона распределения.

Если СВ дискретные, то

Если СВ X и Y непрерывные, то

Определение.

называется регрессией Y на x.

называется регрессией X на y.

Графики этих зависимостей от x и от y называются линиями регрессии или кривыми регрессии.

Пример.

Y X	0	2	5	Pi
1	0,1	0	0,2	0,3
2	0	0,3	0	0,3
4	0,1	0,3	0	0,4
Pj	0,2	0,6	0,2	

Построить линии регрессии Y на x и X на y.



Замечание.

Для независимых СВ линии регрессии Y на x и X на y параллельны координатным осям так как МО каждой из них не зависит от того, какое значение приняла другая.

Линии регрессии могут быть параллельны координатным осям и для зависимых СВ, когда МО каждой из них зависит от того, какое значение приняла другая.

Так как все моменты начальные и центральные любых порядков представляют собой МО, то можно говорить об условных моментах. Например об условных дисперсиях , .

§ 8. Двумерные нормальные распределения.

Определение

Нормальным законом распределения на плоскости называется распределение вероятностей двумерной СВ , если

Итак нормальный закон на плоскости определяется 5-ю параметрами: .

Убедимся в том, что если компоненты X и Y не коррелированны, то они тогда и не зависимы.

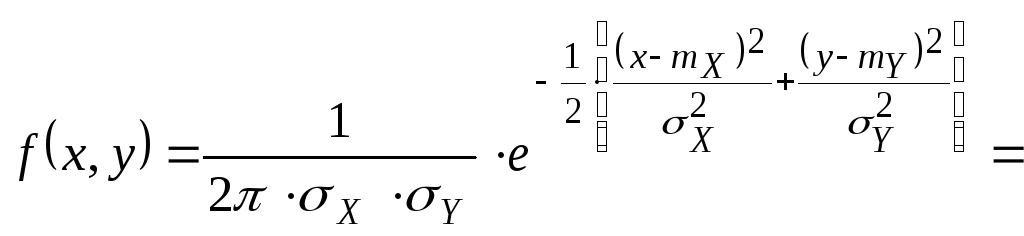
Замечание

Для нормально распределенных компонент двумерной СВ понятие независимости и некоррелированности равносильны.

Найдем условные законы распределения СВ X и Y воспользовавшись формулами.

.

.

Как легко видеть , каждый из условных законов распределения является также нормальных с условным МО и условной дисперсией вычисляемым по формуле:

Замечание.

Из двух формул для условного МО видно, что для системы нормально распределенных X и Y, линии регрессии Y на x и X на y представляют собой прямые линии, то есть регрессия всегда линейна.

В геометрической интерпретации график линейной формулы плотности представляет собой холмообразную поверхность.

.

Сечение поверхности плоскостями параллельными плоскости XOY представляют собой эллипсы.

Глава 8

Законы распределения функций СВ

§ 1. Закон распределения функции одного случайного аргумента.

X	x1	x2	…	xn
P	p1	p2	…	pn

Y	y1	…	ym
P		…

1)	X	–2	–1	0	1	2
	P	0,1	0,15	0,3	0,05	0,4

Y	–8	–1	0	1	8
P	0,1	0,15	0,3	0,05	0,4

2)	X	–2	–1	0	1	2
	P	0,1	0,15	0,3	0,05	0,4

Y	0	1	4
P	0,3	0,2	0,5

Пусть теперь СВ X – непрерывна и функция – функция плотности.

Найдем закон распределения СВ Y, но при этом ограничимся случаем, когда функция строго монотонна, непрерывна и дифференцируема в интервале (a, b) всех возможных значений СВ X.

СВ Y будет определяться по формуле .

монотонно возрастает на (a, b).

– функция обратная к функции .

.

Лекция № 17

1) – монотонно возрастает

2) – монотонно убывает на (a; b)

Дифференцируя по y, получим

Пример 1

СВ Х распределена непрерывно с функцией плотности .

Пусть .

Найти – ?

(*)

Пример 2

СВ . Пусть . Выяснить, как выглядит функция плотности и какому закону она подчиняется.

.

Итак в результате линейного преобразования нормально распределенной СВ Х, получается СВ Y распределенная по нормальному закону с параметрами . ().

§ 2. Функции от многомерных СВ. Формула композиции.

Функция от многомерной СВ определяется точно также, как и функция от одномерной СВ.

Мы рассмотрим это понятие на примере двумерной СВ.

Пусть на вероятностном пространстве (, A, P), задана двумерная СВ (X, Y). Предположим, что у нас имеется измеренная числовая функция числовых аргументов X и Y.

СВ , назовем функцией от двумерной СВ (X, Y).

а) Функция от двумерной дискретной СВ (X, Y) снова является дискретной СВ, принимающей значения с вероятностями .

Чтобы построить ряд распределения СВ надо:

1) Исключить все те значения , вероятность которых равна нулю;

2) Объединить в один столбец все одинаковые значения , приписав этому столбцу суммарную вероятность.

Пример

Рассмотрим СВ –суммарное число успехов в двух независимых опытах с одной и той же вероятностью p в каждом отдельном опыте. Тогда , где – количество успехов в первом опыте, а – количество успехов во втором опыте, а .

Поскольку и принимают только два значения 0 или 1, тогда :

	0	1	2
P	q2	2pq	p2

б) В случае когда СВ (X, Y) непрерывного типа с плотностью , функция распределения будет определяться формулой

Область интегрирования здесь состоит из всех точек (x, y) для которых .

Особо важным для практики представляется случай, когда X и Y – независимые СВ, а функция Z=X + Y, тогда .

Получается так называемая формула композиции.

(*)

Интеграл (*) вычисляется, как повторный, поэтому

.

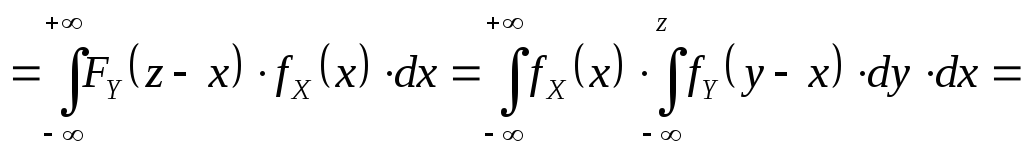
Дифференцируя по z получаем

– формулы композиции (свертки).

С помощью этих формул легко выражаются формулы плотности и функции распределения суммы независимых СВ.

Пример.

Пусть X и Y – независимы. – функция распределения Х, а Y имеет плотность

Получить функцию распределения и функцию плотности суммы X + Y.

;

Так как производная интеграла по переменной z равна значению подынтегральной функции от верхнего предела умноженную на производную по z от верхнего предела , минус значение подынтегральной функции от нижнего предела на производную по z от нижнего предела.

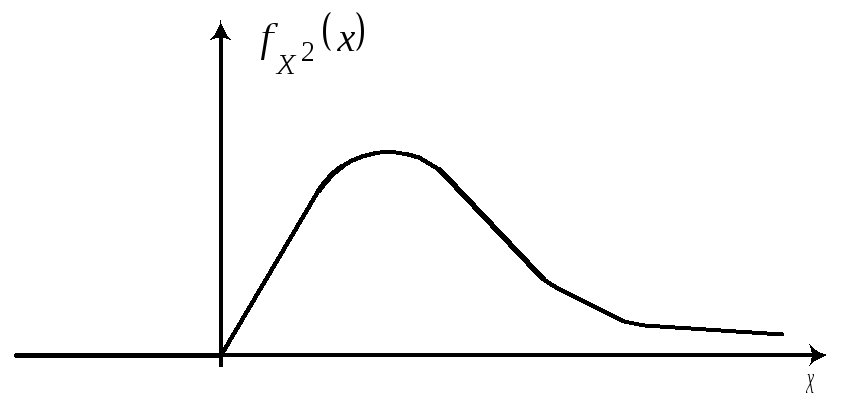
§ 3. Распределение ². (“хи-квадрат”).

Пусть , тогда – –называется СВ распределенной по закону ² с k степенями свободны.

,

, .

Распределение ² определяется одним параметром числом степеней свободы. С увеличением степеней свободы распределение ² медленно приближается к нормальному.

На практике при k > 30 считают, что , где .

Для СВ, имеющей ² распределение существуют таблицы квантилей.

§ 4. Распределение Стьюдента.

Пусть .

V– независимая от Z СВ, которая распределена по закону ² с k степенями свободы.

Рассмотрим СВ .

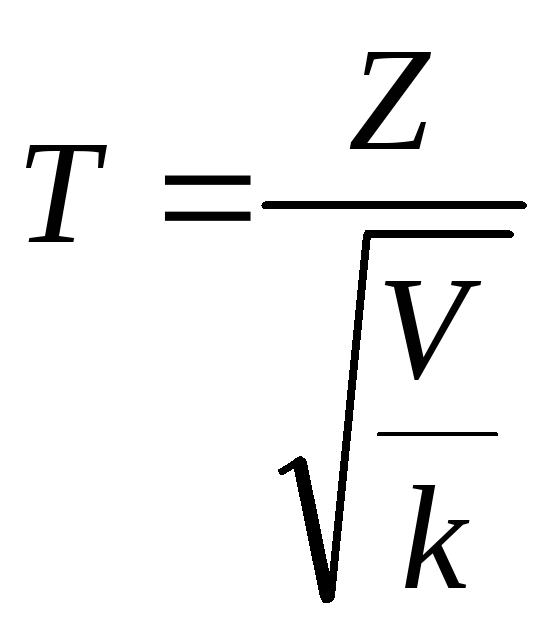СВ Т имеет распределение, которое называется t–распределением или распределением Стьюдента с k степенями свободы.

t–распределение определяется одним параметром – числом степеней свободы.

С возрастанием числа степеней свободы t–распределение асимптотически (довольно быстро) приближается к стандартному нормальному распределению с параметрами (0; 1).

Для СВ, имеющих распределение Стьюдента, имеется таблица квантилей, причем в силу четности .

§ 5. Распределение Фишера.

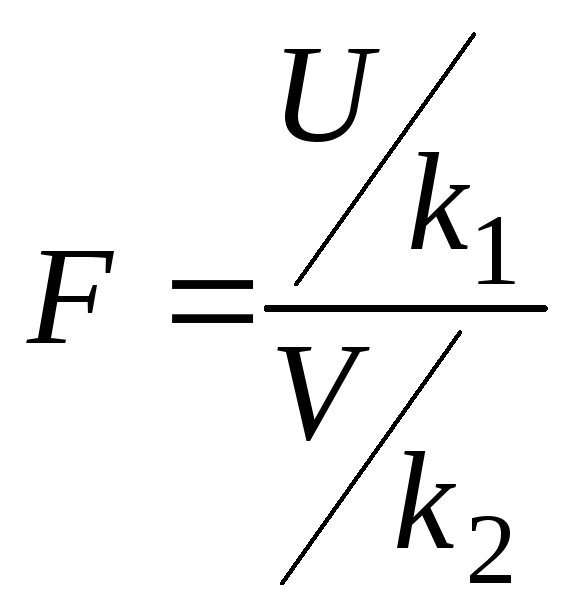Если U и V независимые СВ, распределенные по закону ², , , тогда имеет распределение, которое называется F–распределением или распределением Фишера со степенями свободы k₁ и k₂. (.

F–распределение определяется двумя параметрами k₁ и k₂ и существует таблица квантилей.

.