Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци23

Лекция 23.

 6.6. Проверка гипотез о законе распределения.

 6.6.1. Общие положения, постановка задачи.

~ а – вектор параметров, которыми определяется данное распределение.

Нужна статистика, подходящая как мера расхождения между и .

Обозначим - эмпирическая функция распределения.

1. Одна из мер: 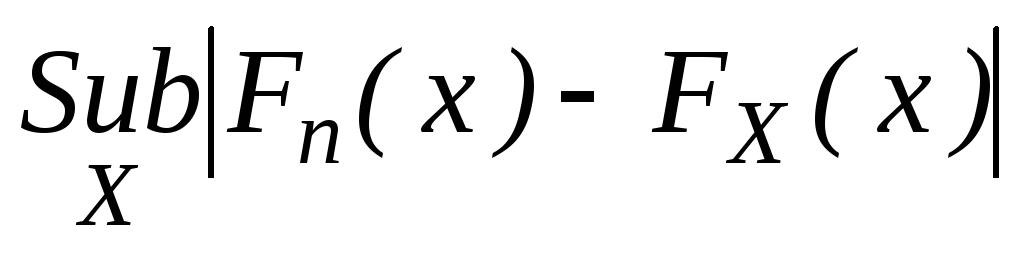- мера расхождения.

2. Еще одна мера – на основе сравнения частот попадания на интервал.

Теорема Гливенко (аналог теоремы Бернулли): , .

Следствие. (в вероятностном смысле).

В любом случае любая статика Z становиться функцией

Всякая гипотеза H₀ становиться сложной.

Теорема Колмогорова. Пусть статистика , тогда

- функция распределения Колмогорова.

(практически при n>20 это теорема выполняется при непрерывной

K(t) – затабулировано.

 6.6.2. Критерий согласия ².

дискретная  разряды для сравнения частот– это возможные Генеральная X значения x.

непрерывная  разряды – это интервалы, получаемые при

интервальном представлении выборки.

Случай 1. X- непрерывная

1) Гипотеза H₀ – простая, т.е. полностью определяется законом распределения X.

F_X(x)

1

I₂ I₃ I_L

| | | |

а₁ а₂ а₃ …………………а_L-1 x

Т.к. Н₀ – простая 

Пусть получена выборка:

Распределение по интервалам: пусть - число выборочных значений, попали в .

(1)

Рассмотрим меру расхождения.

, где

Теорема Пирсона. Если Н₀ – простая, , , то

~

Преобразуем (2): .

Обозначим: (3)

- номинальное распределение.

 при больших n ~

 Z_k – стандартизованная пуассоновская величена.

Т.к. , то по теореме Пирсона Z~.

Почему теряется одна степень свободы?

Если на Z_k накладываются некоторые условия (следует из дополнительной связи), то теряется первая степень свободы.

Из (3) следует, что . Учитывая (1), получаем:

Из таблицы  расхождение дольше при малых .

Z_выб=0,49

Из таблицы находим что соответствует уровню значимости

При гипотеза Н­_0­ будет приниматься.