Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци14

Лекция 14

§4.4 Законы распределения функций

Пусть X - случайная величина, Y = (X), где y=(x) - заданная действительная функция.

Случай 1. Если X-СВДТ  P{Y=y_k}=, где I_k={i | (x)=y_k}.

Случай 2. Пусть X-СВНТ. Тогда возможны 2 случая

1) (x) - монотонная. (x), может быть либо монотонно возрастающей, либо монотонно убывающей

2) (x) - не монотонная

Для определенности рассмотрим случай, когда (x) монотонно возрастающая.

1) ищем функцию распределения F_Y(y)=(по определению)=P{Y<y}

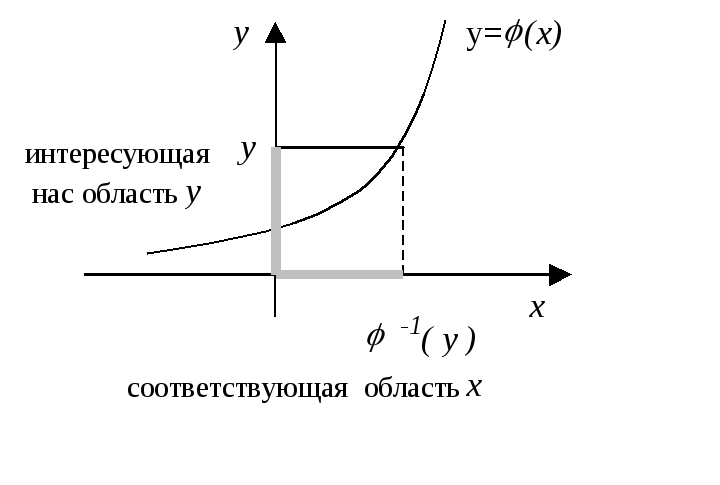
Задача: перевести вероятность с оси x на ось y.

Таким образом, P{Y<y}=P{X<^--1(y)}=Fx(^--1(y))

2)Находим плотность распределения вероятности новой случайной величины Y:

f_X(y)==

Рассмотрим монотонно убывающую функцию (x), тогда:

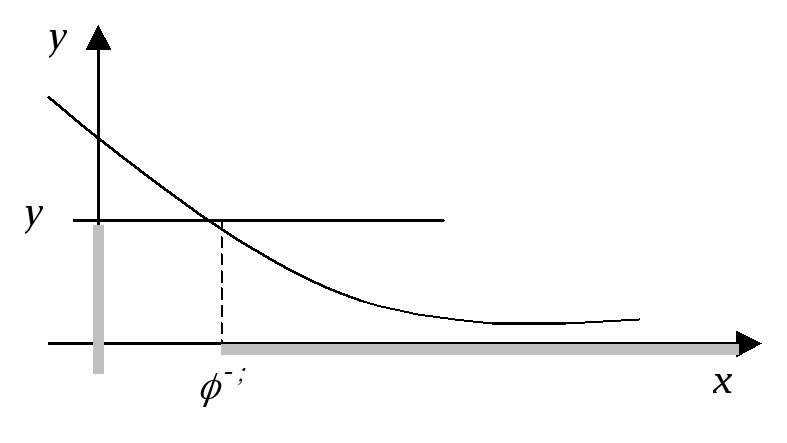
F_Y(y)=(по определению)=P{Y<y}=P(X>^--1(y)}=1-P{X<^--1(y)}=1-Fx(^--1(y)) 

f_Y(y)=

Рассмотрим случай, когда (x) не монотонная.

Пример 1. Пусть X~N(0,1), Y=X³, найти плотность f_Y(y).

Решение.

Заметим, что функция y=(x)=x³ - монотонно возрастающая на всей числовой оси.

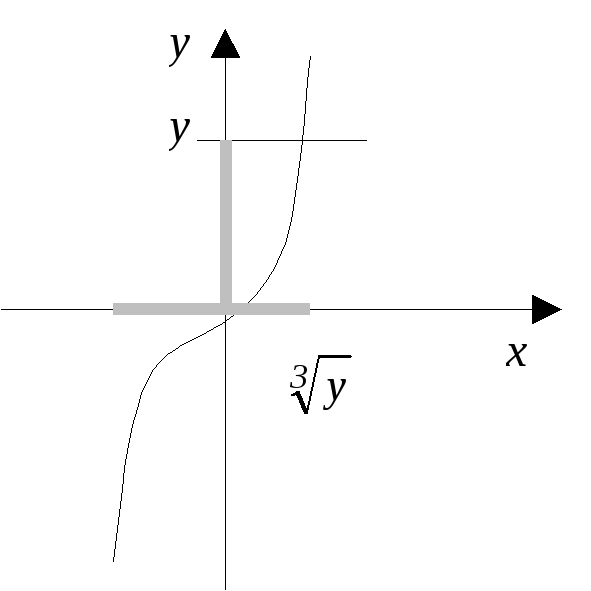
F_Y(y)=P{X<}=() ( - интервал вероятности, специальная функция нормального распределения)

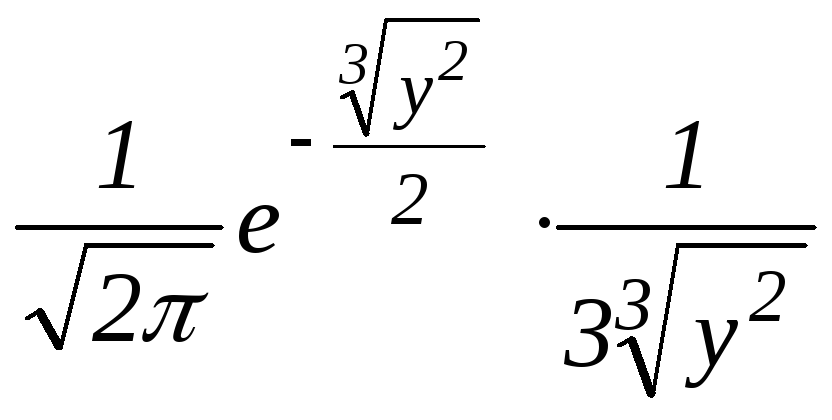(x)=­, f_X(y)===, y0

Рассмотрим случай, когда (x) не монотонная