
Лекции / Лекции (МП-3 Земсков) / Лекции (word) / Лекци20
.docЛекция 20
![]() -
задано,
(1)
-
задано,
(1)
![]() ~
~
![]()
![]() Ф
Ф![]() -1=
-1=![]() ,
,
Ф=![]() .
.
В данном случае ищется квантиль.
Определение. Квантиль порядка р для данного распределения есть число tp:
![]()
![]()
Определение.
Критическая
точка порядка
р![]() :
:
![]()
![]()
![]()
Из
(1)
![]()
![]() (2)
(2)
- доверительный интервал для математического ожидания.
Говорят: «Полученный интервал накрывает неизвестные значения математического смещения»
![]() ,
при
,
при
![]()
Формально можно было сделать так:
![]() ;
Делим на
;
Делим на
![]()
![]() ,
,
![]()
U~N(0,1)
U~N(0,1)
Для построения доверительного интервала нужна подходящая статистика.
Определение.
Статика
![]() ,
называется подходящей
для построения доверительного интервала
для неизвестного параметра ,
если выполнены два условия:
,
называется подходящей
для построения доверительного интервала
для неизвестного параметра ,
если выполнены два условия:
-
закон распределения Z1 известен и не зависит от ;
-
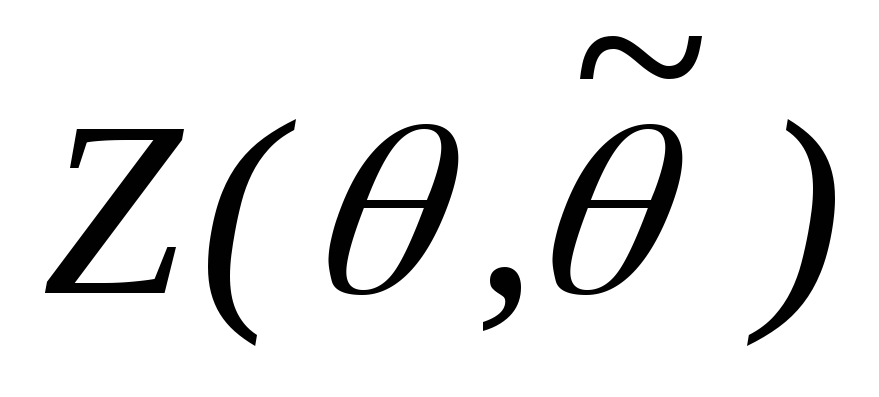 как
функция от
- непрерывна и строго монотонна.
как
функция от
- непрерывна и строго монотонна.
Определение. Пусть найдены такие 1 и 2, что:
-
 1
1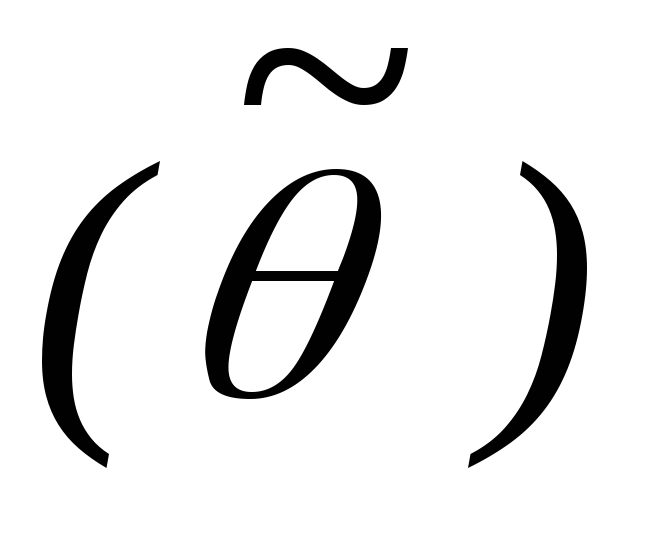 <
<
 2
2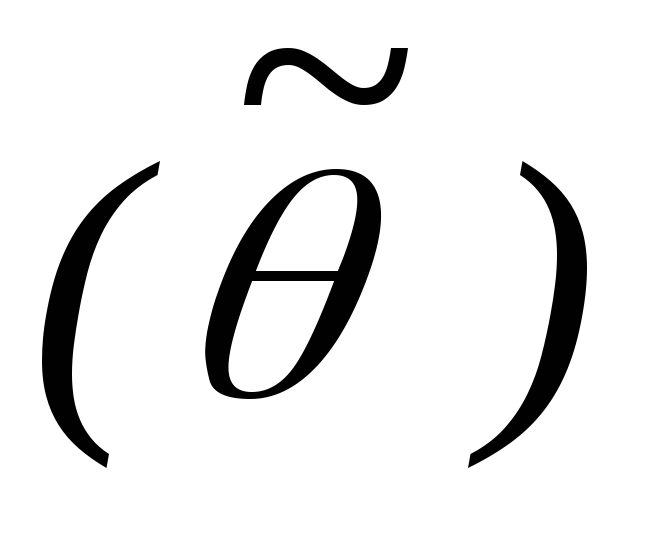 для любой выборки;
для любой выборки; -
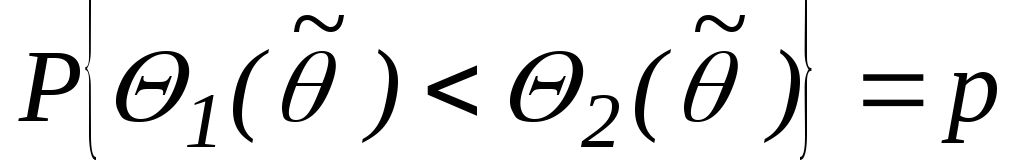 ;
; -
Интервал
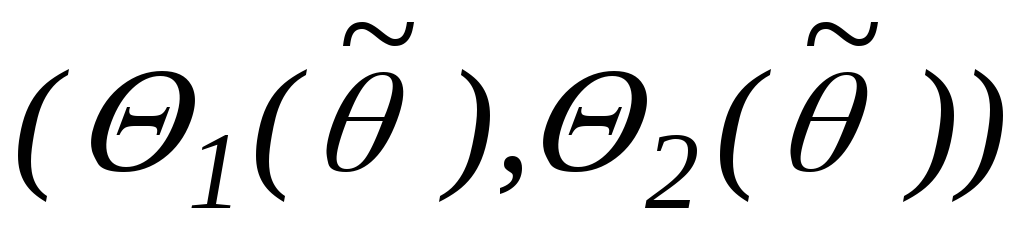 -
наименьшей длины для данного распределения
статики, тогда интервал
-
наименьшей длины для данного распределения
статики, тогда интервал
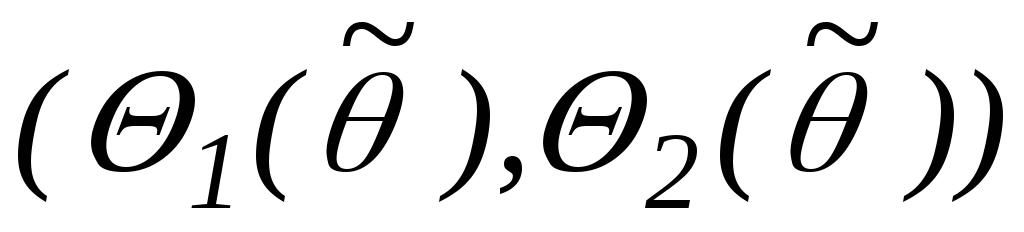 называется
доверительным интервалом с вероятностью
накрывающим независимый параметр
называется
доверительным интервалом с вероятностью
накрывающим независимый параметр

Рассмотрим два типа распределения статики.
-
Р
fZ(z)-плотность
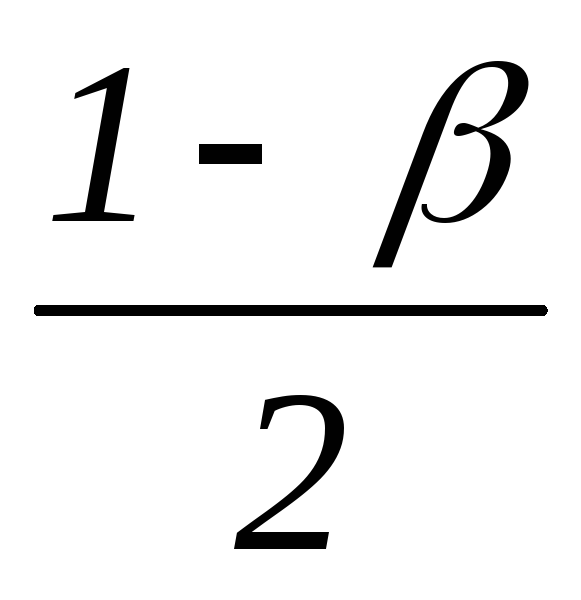
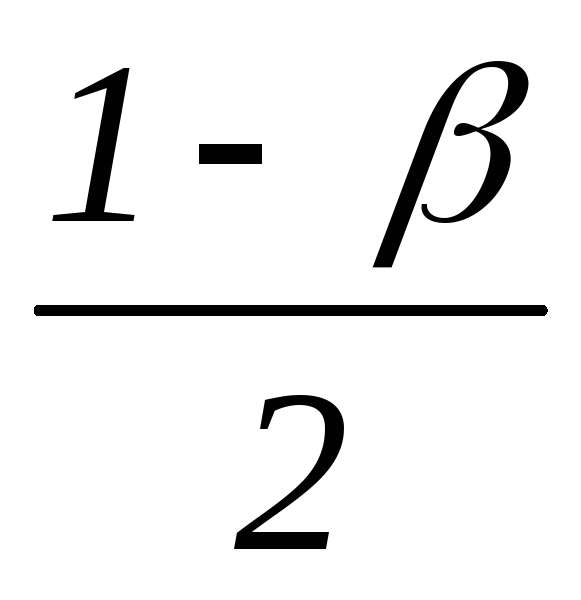
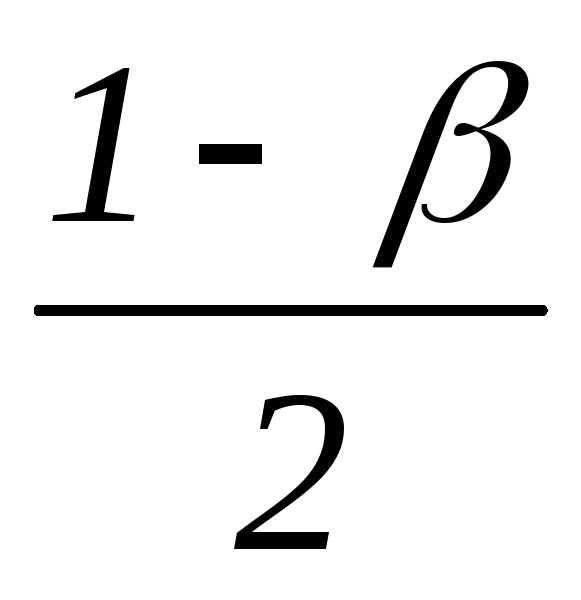



 аспределение
(N, St)
аспределение
(N, St)
z
![]()
![]()


Выберем симметричный интервал, площадь под графиком на ней равна .
![]() =
=
Учитывая,
что
![]() - строго монотонно зависит от
, можно
разрешить неравенство
- строго монотонно зависит от
, можно
разрешить неравенство
![]() относительно
получаем доверительный интервал.
относительно
получаем доверительный интервал.
-
Распределение типа "хи-квадрат"
fZ(z)
![]()
![]()



В
z1
z2 z


 ыбираем
интервал так, чтобы на концы попадало
ыбираем
интервал так, чтобы на концы попадало
![]() .
.
![]() ;
;![]() - квантили из распределения статистики
Z
- квантили из распределения статистики
Z
Пример 1. Пусть X~N(m,2) m и 2 – неизвестны. Построить доверительный интервал для m.
![]() Статику U
использовать нельзя, так как
- неизвестно.
Статику U
использовать нельзя, так как
- неизвестно.
Воспользуемся W-статикой.
![]() ~St(n-1)
~St(n-1)
В (2) сделаем
замену:![]()
![]() (3)
(3)
В (3) – длина интервала – случайная величина.
При увеличении n
квантили перейдут
к квантилям нормального распределения.
![]()
Пример 2. (продолжение). Построить доверительный интервал для 2.
![]() Подходящей статикой
является V2,
Подходящей статикой
является V2,
![]() ~
~
![]()
Имеем II-ой тип распределения. Находим точки:
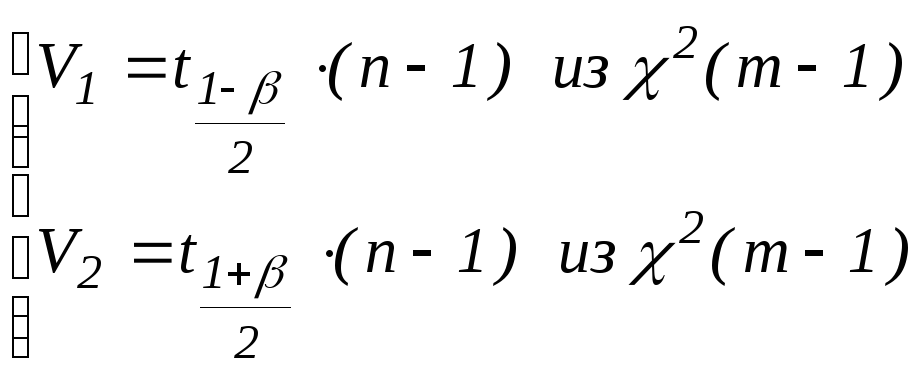 (4)
(4)
Получим: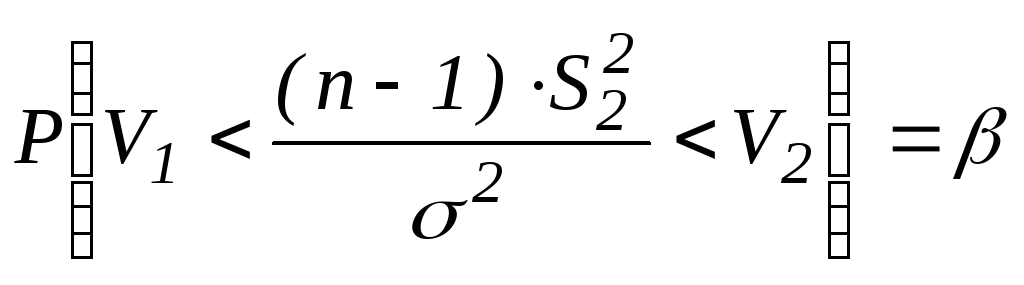 .
.
![]() -
монотонно убывающая. Решим неравенство,
учитывая это.
-
монотонно убывающая. Решим неравенство,
учитывая это.
V2(2)
V2


2
V1![]()
![]()



![]() (5)
(5)
*** Исследовать зависимость длины интервала от объема выборки, воспользоваться асимптотической нормальностью χ2 и выразить квантиль χ2 -распределения через квантиль нормали.
Стандартизация
:
![]() ~N(0,1)
~N(0,1)
![]()
![]() т.к.
нормали.
т.к.
нормали.
![]()
Замечание 1. Если математическое ожидание известно, то следует воспользоваться не статистикой V2, а статистикой V1.
![]() ~
~![]()
Замечание 2. Чтобы получить доверительный интервал для , а не 2 в условиях примера 2, надо извлечь корень и неравенства (5)
![]() (6)
(6)
Закон сохранения
вероятностей для монотонных статик:
В силу того, что статистика и корень
монотонны, то
![]()
Пример 3. Пусть Х~B(1, p) . Построить доверительный интервал для р.
![]() Наилучшей
оценкой для р
является
Наилучшей
оценкой для р
является
![]() .
Подходящая статистика для построения
доверительного интервала является:
.
Подходящая статистика для построения
доверительного интервала является:![]()
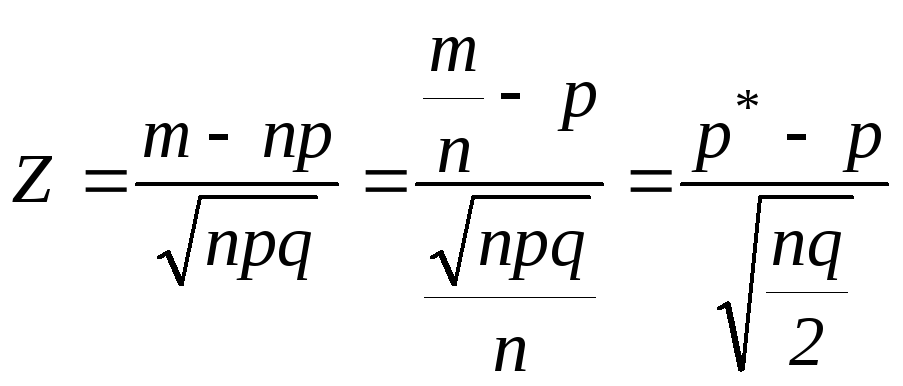 ~N(0,1)
(по
теореме Муавра-Лапласа).
~N(0,1)
(по
теореме Муавра-Лапласа).
Проверим условие (2) подходящей статистики.
Z(p) – сложная зависимость.
![]() ,
,
![]()
Т.к. закон распределения статистики Z относится к первому типу, то
![]() ,
,
![]()
Взведем в квадрат:
![]() Если поставить
знак равно, то будет уравнение эллипса,
сильно вытянутое вдоль биссектрисы.
Если поставить
знак равно, то будет уравнение эллипса,
сильно вытянутое вдоль биссектрисы.
При n>>1 найдем корни уравнения:
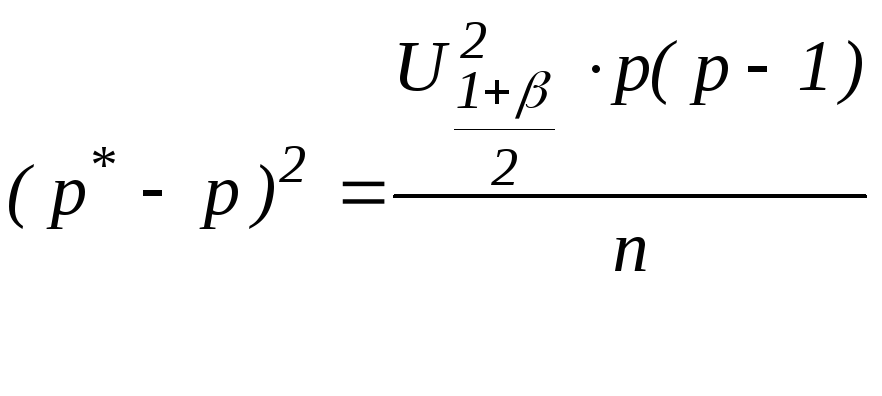
![]()
Ответ:
![]() только при больших n.
только при больших n.
![]()
