Лекция 18

Проверим несмещенность:

=

=

==

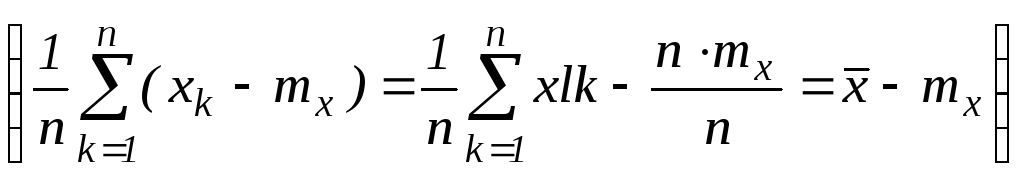(1)

Пример 3. Показать, что можно преобразовать к виду:

(2)

где

= оценка смещенная, но при стремиться

к  Говорят, что оценка асимптотически смещена.

Вводят следующую замену:

Замечание. Потеря одной степени свободы объясняется тем, что мы не знали математическое ожидание и оцениваем его по выборке. Если бы оно было известно, то несмещенной оценкой дисперсии была бы следующая величина:

Проверим состоятельность оценки дисперсии:

Легко видеть, что две суммы в (2) скоррелированны.

при

2. Методы моментов.

Метод подстановки применяется обычно для оценки моментов, медиан и т.п. Метод моментов применяется для оценки параметров распределения. Пусть ~, - вектор параметров, независимая величина. Необходимо оценить по выборке.

Пусть =(₁, ₂)  составим систему уравнений по методу подстановки следующим образом:

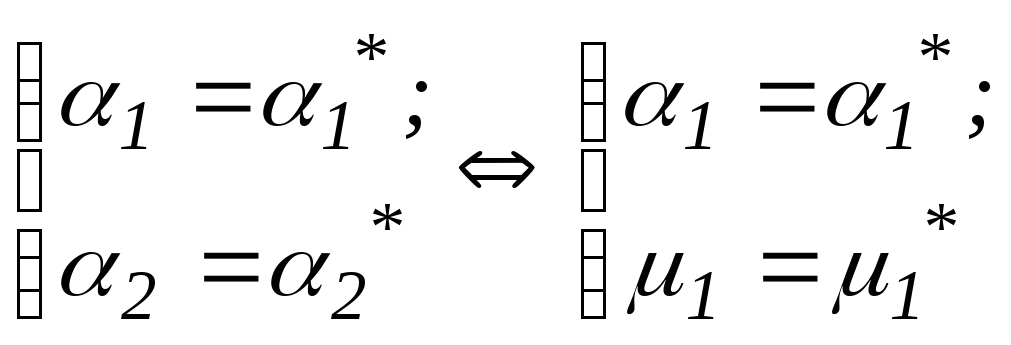(3)

Смысл: все параметры в левой части, а все известное в правой. Считаем оценку по методу моментов.

Пример 1. Пусть Х~R(a,b).Оценить a и b по методу моментов.

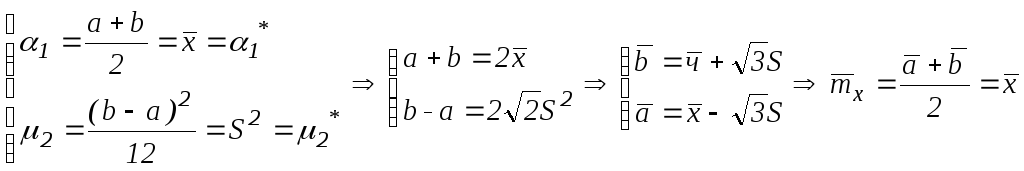
Пример 2. (дискретный случай). Пусть Х~B(m,p), р - неизвестно. Оценить р по методу моментов, проверить свойства.

Требуется одно уравнение:  , где m – число

опытов.

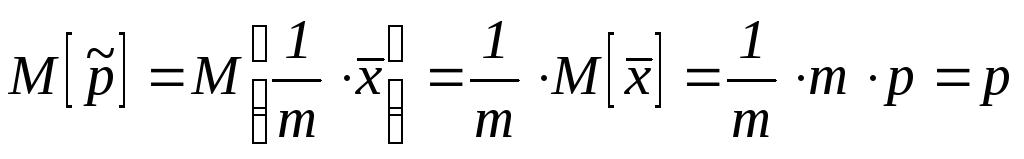
 несмещенность;

так как n 0 

состоятельность доказана  ­- состоятельная оценка

2. Метод максимального правдоподобия.

Постановка задачи та же.

Вспомним: выборочный вектор – где X_i одинаково распределены и независимы. (x₁,x₂,…,x_n) – реализация выборочного вектора.

Определение. Функция правдоподобия выборки

• ( для непрерывного генерального) – это есть плотность распределения выборочного вектора, взятая в точке его реализации;

• ( для дискретного генерального) – вероятность реализации данного выборочного вектора.

Обозначение: (4) L_x(Q)=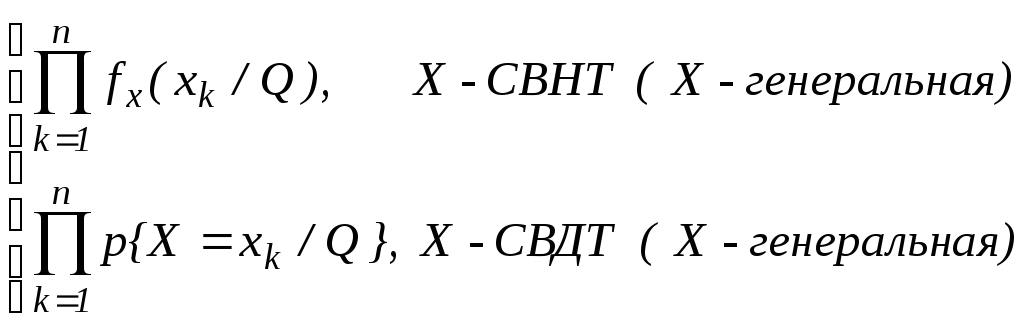

Пример 3. Пусть Х~N(m,²). Оценить в по ММП.

Пусть получена выборка х₁, х₂,…, х_n. Составим функцию правдоподобия:

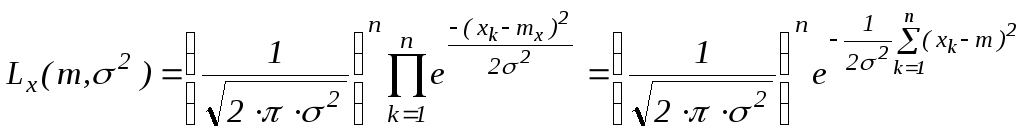
Главный принцип ММП.

Определение. Оценками метода правдоподобия называются такие значения параметров, которые доставляют max L_x(m, ²) т.е. дана задача на экстремум:

max L_x(m, ²)max.

Необходимым условием экстремума является равенство нулю всех производных первого порядка. Удобнее рассматривать экстремум не самой функции, а ее логарифма.

Необходимое условие экстремума:



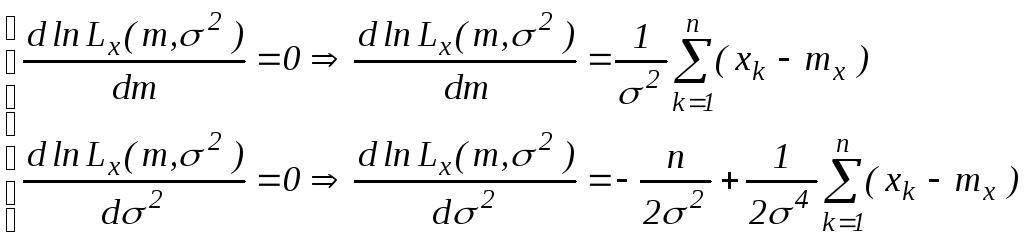
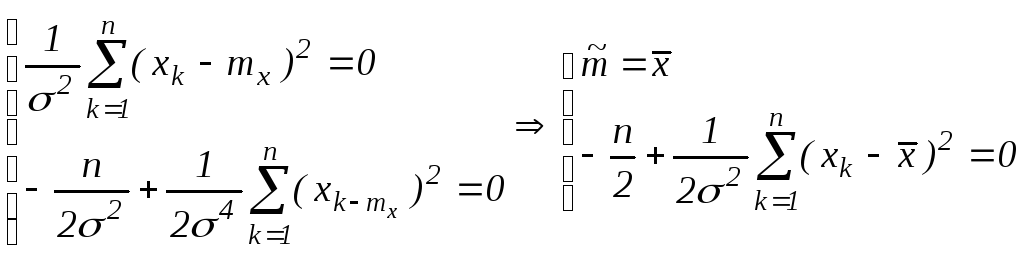
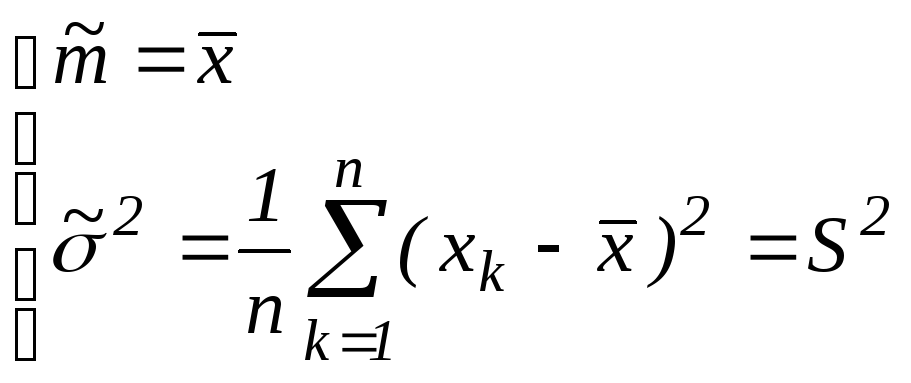 - оценка асимптотически несмещенная

Пример 4. Пусть Х~B(1,p). Оценить р по методу правдоподобия.

Пусть получена выборка х₁, х₂,.., х_n . Все значения реализуются независимо. Пусть получено m единиц и (n-m) нулей.

- частота испытаний.

При некоторых дополнительных условиях на функцию правдоподобия выборки справедливо следующее неравенство Крамера-Рао:

(5), где In()- информация по Фишеру относительно неизвестного параметра  , содержащегося в выборке.

Определение. Абсолютно эффективной называется оценка, достигающая нижней границы неравенства Крамера-Рао, т.е.