Лаб.раб. по механике / Лабораторная работа № 10

ЛАБОРАТОРНАЯ РАБОТА №10

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ РОТОРА

ЭЛЕКТРОДВИГАТЕЛЯ И ИОИЕНТА СИЛ

СОПРОТИВЛЕНИЯ

ВРАЩЕНИЮ

Цель работы: ознакомиться с одним из методов экспериментального определения момента инерции и момента сил.

Оборудование: экспериментальная установка, секундомер, штангенциркуль.

КРАТКАЯ ТЕОРИЯ

Общую теорию вращательного движения изучите по лабораторной работе № 8.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА. ТЕОРИЯ МЕТОДА И

МЕТОДИКА ИЗМЕРЕНИЙ

У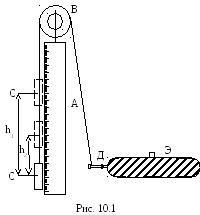становка (рис. 10.1) состоит из длинной вертикальной шкалы А, на верхнем конце которой укреплен блок В, вращающийся вокруг горизонтальной оси с очень небольшим трением. Через блок перекинут шнур, к одному концу которого крепится груз С массой m. Другой конец шнура наматывается на насадку вала Д электродвигателя Э. Груз С поднимается на некоторую высоту h, и вся система получает запас потенциальной энергии .

Если вал Д электродвигателя Э освободить, то груз С начинает опускаться, приводя ротор электродвигателя во вращение, которое можно считать равноускоренным. В этом процессе потенциальная энергия груза С расходуется на преодоление силы трения F и на увеличение кинетической энергии системы. Поэтому для нижнего положения груза С имеем:

(10.1)

где - скорость падения груза С; J – момент инерции ротора; - угловая скорость ротора; - кинетическая энергия вращения ротора; - работа по преодолению силы трения ротора.

Силу трения F можно вычислить следующим образом. Ротор, благодаря запасенной энергии, продолжает вращаться и поднимает груз на высоту <. На высоте система обладает потенциальной энергией . Убыль потенциальной энергии численно равна работе по преодолению силы трения вала

откуда

(10.2)

так как движение равноускоренное, то

, ,

где - время опускания груза. Тогда

(10.3)

Угловая скорость равна , где r – радиус насадки вала. Следовательно,

(10.4)

Подставляя значения из (10.2), (10.3), (10.4) в (10.1), имеем

После несложных преобразований получаем выражение для вычисления момента инерции ротора:

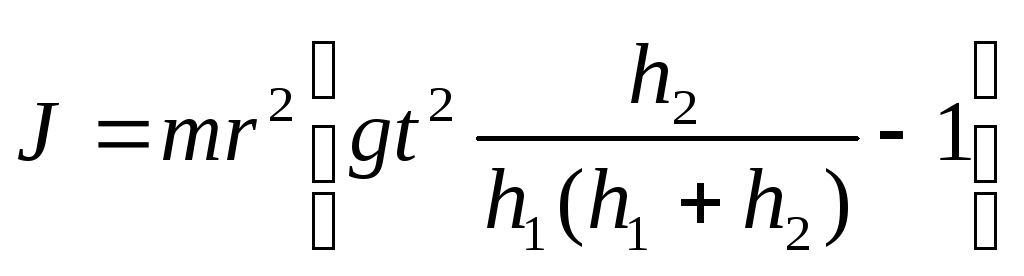(10.5)

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ РОТОРА

Для этого в данной работе штангенциркулем измеряем диаметр насадки вала, определяем его радиус. Вращением вала поднимаем груз до высоты h₁ и измеряем ее. Отпускаем груз и определяем высоту h₂, на которую поднимается груз вследствие вращения ротора электродвигателя. При помощи секундомера измеряем время падения груза с высоты h₁ не менее 5 раз. Зная массу груза (см. груз), вычисляем по формуле (10.5) значение момента инерции.

ПРИМЕЧАНИЕ: необходимо научиться пускать груз так, чтобы он не получал колебательного движения, следить за тем, чтобы шнур был намотан на вал в один ряд.

ОПРЕДЕЛЕНИЕ МОМЕНТА СИЛ СОПРОТИВЛЕНИЯ

ЭЛЕКТРОДВИГАТЕЛЯ

Для определения момента сил сопротивления электродвигателя подключаем электродвигатель к сети, предварительно сняв с вала насадку. Отключаем электродвигатель и одновременно включаем секундомер, по которому определяем время до полной остановки ротора.

В данном случае

(10.6)

(10.7)

(10.8)

где - угловое ускорение, - угловое перемещение тела, - угловая скорость.

Подставляя в формулу (10.8) значения из формул (10.6) и (10.7), получаем . Так как , то имеем

(10.9)

выражение для вычисления момента сопротивления электродвигателя.

ЗАДАНИЯ

1. Изучите теорию данного вопроса.

2. Изучите экспериментальную установку.

3. Оцените приборные ошибки прямых измерений.

4. Определите момент инерции ротора электродвигателя по формуле (10.5).

5. Определите момент сопротивления электродвигателя по формуле (10.9).

6. Рассчитайте относительную и абсолютную погрешности измеряемых величин.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. Дайте определение основных кинематических и динамических вращательных физических величин.

2. Напишите и объясните уравнение второго закона Ньютона для вращательного движения.

3. Как определяется кинетическая энергия вращающегося тела?

4. Получите формулу (10.5).