
Лекции / 19
.docВыборочный коэффициент ранговой корреляции Спирмена и проверка гипотезы о его значимости.
Для оценки конечной зависимости СВ X
и Y используются
коэффициенты ранговой корреляции
Спирмена и Кенделя .Если между двумя СВ
высокая ранговая корреляция, то достаточно
контролировать только одну из этих СВ.
Проранжируем СВ X и Y.
Расположим объекты по признаку Х в
порядке ухудшения качества Х и объекту,
стоящему на i-ом месте
припишем ранг![]() .
Расположим теперь объекты по признаку
Y и в порядке ухудшения
качества Y и объекту
стоящему на i-ом месте
припишем ранг, но при этом индекс i
равен номеру объекта по признаку х,
т.е запись
.
Расположим теперь объекты по признаку
Y и в порядке ухудшения
качества Y и объекту
стоящему на i-ом месте
припишем ранг, но при этом индекс i
равен номеру объекта по признаку х,
т.е запись
![]() означает чтопо признаку х объект
занимает 5-е место, а по признаку y
–k – 2- e.
В результате получится последовательность
рангов.
означает чтопо признаку х объект
занимает 5-е место, а по признаку y
–k – 2- e.
В результате получится последовательность
рангов.
|
|
|
|
… |
|
|
Y |
|
|
… |
|
Как правило на практике имеет место ситуация, когда ухудшение качества по одному из признаков ведет для одних объектов к улучшению, а для других обектов к ухудшению качества ….
Задача состоит в оценке этой связи, Будем рассматривать признаки как СВ, а их ранги как возможные значения, тогда для оценки связи можно использовать коэффициент корреляции. Коэффициент корреляции Спирмена находится по формуле:
![]()
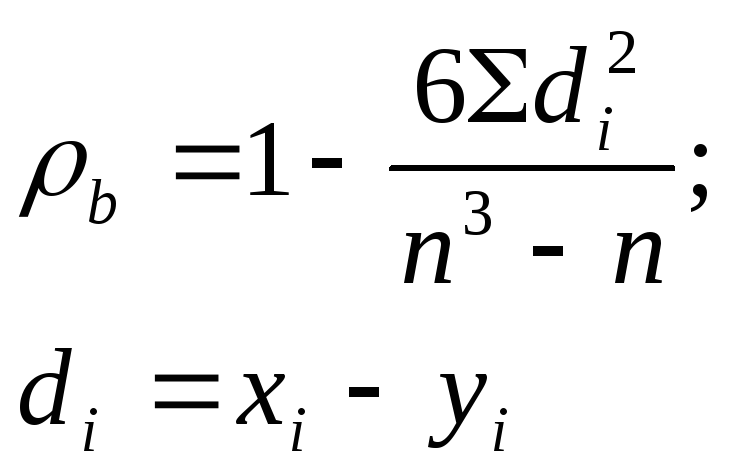
Св-ва коэффициентов ранговой корреляции Спирмена:
-
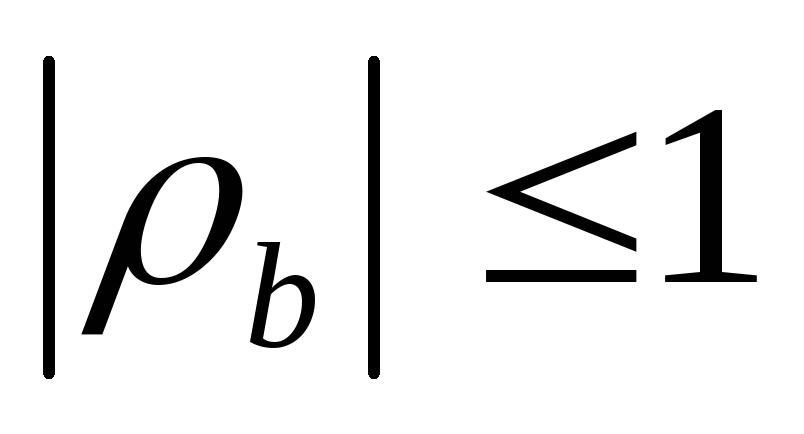
-
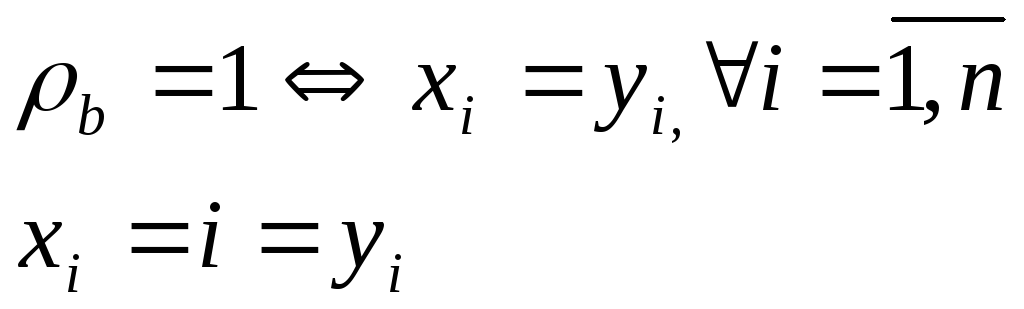 т.е между величинами x и
y прямая зависимость
т.е между величинами x и
y прямая зависимость -
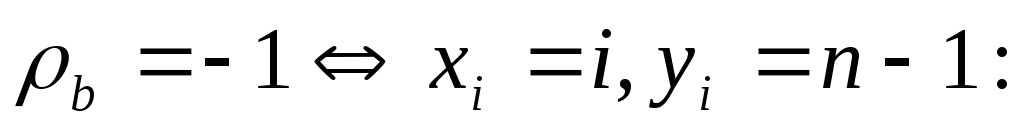 обратная зависимость.
обратная зависимость. -
-1<
 <1
нет ни прямой ни обратной зависимости,
причем чем ближе он к нулю, тем зависимость
меньше.
<1
нет ни прямой ни обратной зависимости,
причем чем ближе он к нулю, тем зависимость
меньше.
Правило проверки гипотезы о значимости коэффициента ранговой корреляции Спирменна при n < 9. (при n<9ествует специальная таблица)
Уровень значимости
![]() ,
,
![]()
![]()
![]() коэффициент
корреляции по Спирману для генеральной
совокупностью
коэффициент
корреляции по Спирману для генеральной
совокупностью
Для проверки гипотезы критическую точку находят по формуле:
![]() по таблице Стьюдента, k=
n-2 по таблицам для
двухсторонней критической области.
Если
по таблице Стьюдента, k=
n-2 по таблицам для
двухсторонней критической области.
Если
![]() то
то
![]() нет оснований отложить, т.е ранговая
корреляционная связь между признаками
не значимая, в противном случае
нет оснований отложить, т.е ранговая
корреляционная связь между признаками
не значимая, в противном случае
![]() отклоняется, т.е
отклоняется, т.е
![]()
![]() ,
принимают
,
принимают
![]() т.е между признаками значения корреляц.
Связь.
т.е между признаками значения корреляц.
Связь.
Пример: По данным признакам, найти
коэффициент ранговой корреляции
![]() по Спирману.
по Спирману.
|
A |
13 |
16 |
20 |
21 |
17 |
14 |
23 |
18 |
11 |
19 |
|
B |
10 |
5 |
9 |
14 |
13 |
15 |
11 |
17 |
7 |
18 |
-
Упорядочиваем объекты по признаку А в порядке ухудшения качества
|
A |
23 |
21 |
20 |
19 |
18 |
17 |
16 |
14 |
13 |
11 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
18 |
17 |
15 |
14 |
13 |
11 |
10 |
9 |
7 |
10 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
6 |
4 |
8 |
1 |
2 |
5 |
10 |
3 |
7 |
9 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
6 |
4 |
8 |
1 |
2 |
5 |
10 |
3 |
7 |
9 |
|
|
-5 |
-2 |
-5 |
3 |
3 |
1 |
-3 |
5 |
2 |
1 |
|
|
25 |
4 |
25 |
9 |
9 |
1 |
9 |
25 |
4 |
1 |

Замечание: если выборка содержит
объекты с одинаковым качеством, то
каждому из них приписывается ранг,
равный среднему арифметическому
порядковых номеров этих объектов по
данному признаку. Если например объекты
одинакового качества по признаку А
имеют порядковые номера 5 и 6 то каждому
объекту приписывается номер:
![]()
