Лекции / 24

24. Общие линейные модели. Регрессионная матрица. Линейная регрессия с Гауссовыми ошибками.

Гауссовыми ошибками МО как и для нормального распределения , i=1,n имеет вид относительно линейной регрессии: (1), где -это случайные погрешности. Запишем эту систему в матричной форме введя замену:

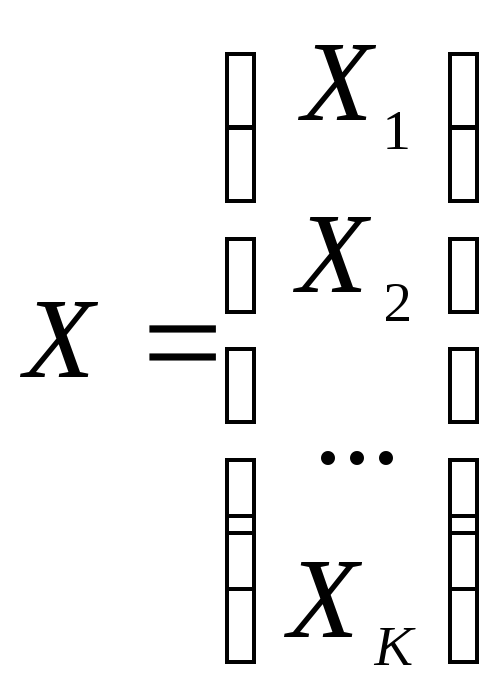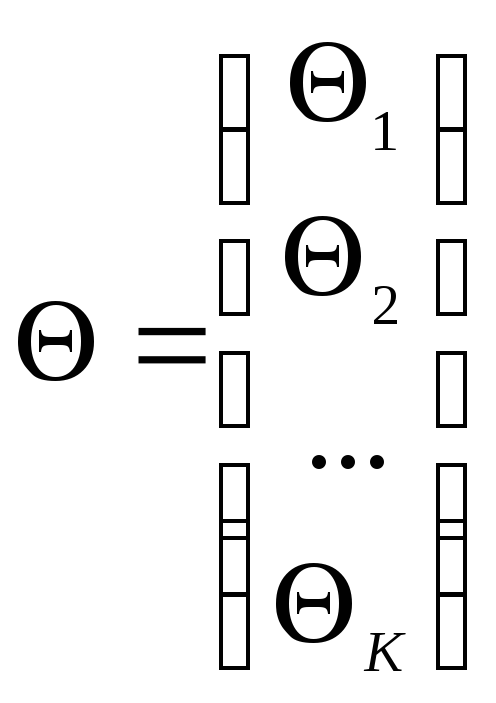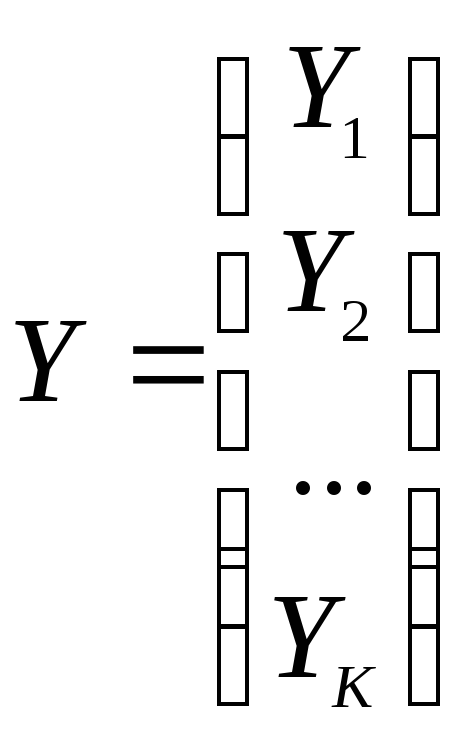, , , тогда (2)

Параметр -оценивается в зависимости от предположенных о природе СВ Х и характеристика распределения . Погрешность -может быть естественной ошибкой свойственной самому эксперименту или может представить собой ошибку измерение значения .

Матрица называется регрессионной матрицей. При этом Выбираются т.о.чтобы столбцы этой матрицы были линейно независимы т.е. ее ранг был равен n . Однако в некоторых случаях при планировании экспериментов элемент матрицы Х выбираются равные только нулю и единицы. В этом случае столбцы могут оказаться линейно-зависимы такую матрицу Х называют матрицей плана.

Модель (1) является достаточно общей например пологая получаем полиноминальную модель.

Модель вида: тоже является разновидностью модели (1) т.к. входят в первой степени. Пусть распределение вектора с независет от матрицы Х и является нормальным причем выборочное среднее этого вектора нулевое т.е. (нуль-вектор). А -неизвестная дисперсия вектора . Одним из методов получения оценки для является МНК(метод наим квадратов). Оценка параметра модели (1) с помощью МНК проводится точно так же как и в §5 Суть ее состоит минимизации суммы

по отношению к .

Положим тогда из ур-я (2) получаем: -эта длина вектора (с одной стороны), а с другой стороны это скалярное произведение . Тогда нужная сумма будет min если будет min длина вектора т.е. величина .Находим производную этой величины:

Т.е. сумма min для являющегося решением ур-я либо ур-я (3)

Из этих ур-й вектор -определяется однозначно если к тому же столбцы матрицы Х линейно-зависимы то существует единственный вектор для которого подставив это значение в равенство (3) получаем так называемое нормальное ур-е, оно имеет вид: (4) т.к. rang Х=n, то матрица -не вырожденная поэтому Ур-е (4)имеет единственное решение: (5) решение (5)называется оценкой МНК.

Остатками называется элемент:

Минимальное значение называется остаточной суммой квадрата и оно равно: (6)

Заметим , чтои е –единственны.

Пример

Пусть и -это независимая СВ со средними значениями и соответственно .Найти оценку МНК для параметра и остаточную сумму квадратов.

Решение :

Для данного примера система (1) имеет вид: 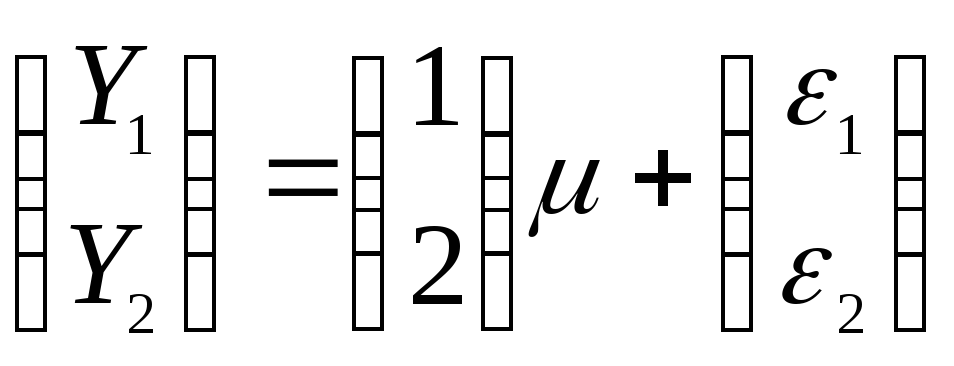здесь

Находим по формуле (5):

Находим остаточную сумму по (6)