Лекции / 26

Вопрос 26. Основные задачи факторного анализа.

Многомерный статистический анализ занимается выявлением скрытых факторов, определяющих изменение некоторой системы, а также классифик. объектов этой системы.

В первом случае система трактуется как многомерная СВ, м/у составляющими кот-й сущ-ет стохастическая связь, а скрытые факторы трактуются как система центрированных некоррелированных СВ.

Выявлением этих скрытых факторов занимается факторный анализ.

Например, при индивидуальном пошиве одежды - это множество мерок, а при пром. изготовлен. одежды – 3 мерки (параметра).

Этот пример наглядно демонстрирует задачу факторного анализа: перейти от системы с большим числом факторов к системе с меньшим числом факторов, изменение которых в значительной мере определяет изменение остальных факторов системы.

В связи с этим важной задачей статистики является задача линейного представления многомерной СВ ч/з СВ-ны меньших размерностей по результатам опытов.

Особенность этой задачи состоит в том, что СВ меньшей размерности не наблюдается и о ней ничего не известно.

Решение поставленной задачи заключается в построении и последующей проверке ее согласованности с экспериментальными данными.

Пусть в результате n- опытов получено m-мерных СВ Y,

т. е. СВ .

Представим ее в виде суммы СВ-н и ошибки измерения ε (многомерной СВ). Если имеется возможность представить СВ Y в виде лин. комбин. r-мерных СВ: , где r< m, то СВ Y можно представить в виде: (1)

Т. обр. приходим к задаче построения модели вида (1) по результатам наблюдения СВ Y.

Методы решения этой задачи составляют содержание факторного анализа.

Б. считать, что СВ некоррелированы м/у собой. Ошибки измерения ε обычно также считаются некоррелированными как м/у собой, так и со СВ-нами .

Задача факторного анализа, т.е. построения модели (1), решается неоднозначно, т.к. любое линейное преобразование СВ, дающее СВ-ну той же размерности , приводит к модели вида (1).

Опр.1. Пусть выполняются следующие условия:

1. СВ –некоррелированы м/у собой (т.е. их корреляционный момент, а зн. и коэффициент корреляции );

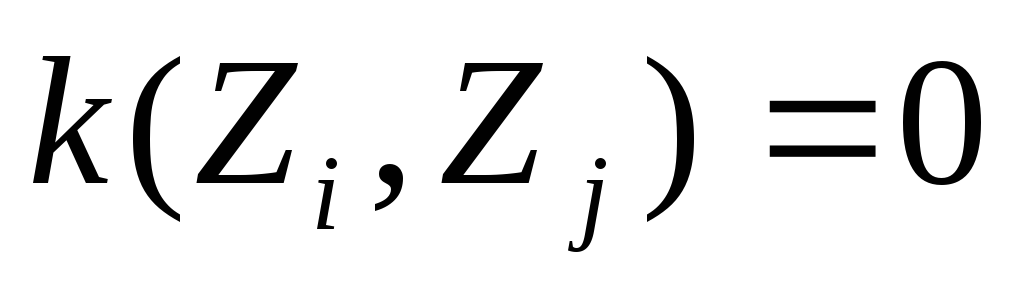2. ошибки измерения ε имеют нулевое МО, некоррелированы с величинами 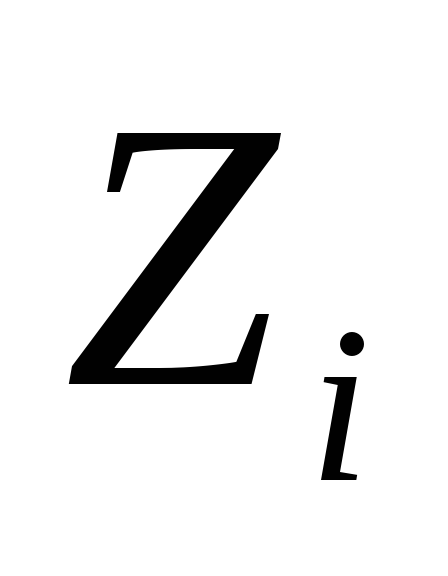и их ковариационная матрица – диагональная;

3. дисперсия СВ : .

Тогда модель (1) наз. факторной моделью, СВ наз. факторами, числа наз. нагрузками СВ на i-тый фактор. Дисперсии СВ наз. факторными дисперсиями.

Зам-е 1. выполнение условия 3) можно добиться путем умножения СВ на соответ-е числа и числа на числа им обратные.

Зам-е 2. Матрица А – ковариац. матр. для СВ , если .

-матрица ковариации, .

Для того чтобы реализовать модель факторного анализа, надо по выборочным данным найти оценки МО СВ , оценки факторных нагрузок и сами общие факторы . Тогда ε в модели (1) определяется как остаток. Существуют методы, позволяющие это сделать, однако они определяют факторы неоднозначно. Поэтому в большинстве случаев при решении практических задач используют метод главных компонент.

МЕТОД ГЛАВНЫХ КОМПОНЕНТ

В отличие от общих факторов, кот. исчерпывали большую часть вариации первонач. факторов, главные компоненты объясняют всю вариацию и определяют однозначно.

Модель главных компонентов имеет вид: (1)

Отсутств. ошибка измерений , поскольку главные компоненты исчерпывают всю вариацию первоначальных факторов.

Главный компонент z_i явл. центрированным, т.е. их МО ; нормированными , т.е. дисперсия ; некоррелированными к СВ-ми.

Обозначим центрированные первоначальные показатели ч/з , тогда модель примет вид: (2)

С целью определить матрицы нагрузок А находят собственные числа и собственные в-ры l ковареацион. матрицы первонач. показателей, т.е. матрице (*)

Из уравнения (3)

Далее из собственных в-ров, соответствующих собственному числу выбирают нормированный, т.е. длина, кот. =1: .

Поскольку собственные в-ры соответствующие различным собственным значениям ортогональны, то матрица L , составленная из этих в-ров так же будет ортогональной. Ей обратная матрица тоже будет ортогональна и равна транспонированной. Поэтому линейное преобразование центриров. первонач. показателей, с номером ортогональной матрицы означает поворот осей, т.е. СВ (4)

Покажем, что нов. показатели не коррелированны, т.к. в силу (4) они центрированы, то получаем:

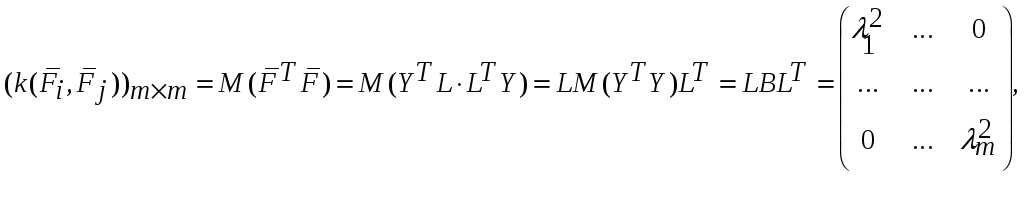т.е. СВ - не коррелированна.

Поскольку ортогональное преобразование сохраняет расстояние, то ; поэтому вся вариация первоначальных показателей = ненормированных главных компонент.

(5)

Из (5) следует. что полная вариация равна сумме собственных значений. На практике поступают следующим образом: главные компоненты перенумерованы в порядке убывания их собственных значений; из всех ненормированных главных компонент оставляют несколько первых, кот. вносят большую часть вариации. Нормированные компоненты получают делением компонент на их среднее квадратичное отклонение, т.е.

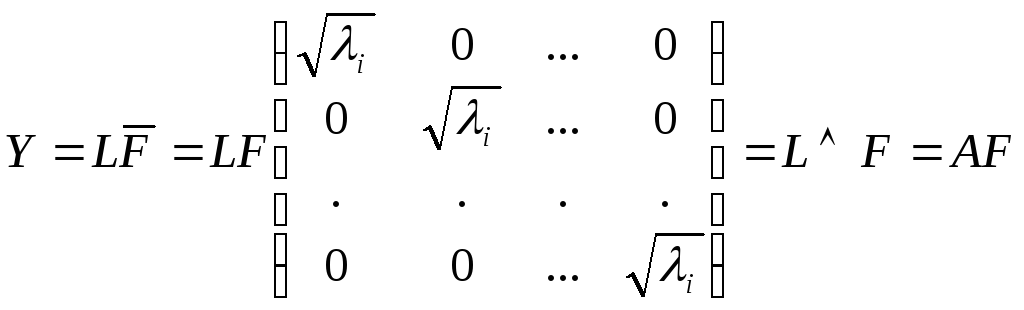, где А- искомая матрица нагрузок. Замечание: на практике описанные выше расчеты выполняются не по теоретическим математическим ожиданиям и ковариационной матрице В, а по их оценкам, получ. на основании выборки.

Методы определения количества главных компонент

В процессе последовательного выделения факторов они включают в себя все меньше и меньше изменчивости. Решение о том, когда следует остановить процедуру выделения факторов, зависит от того, что понимают под случайной изменчивостью. Это решение достаточно произвольно, однако имеются некоторые рекомендации общего хар-ра, позволяющие выбрать число факторов рационально. При каждом следующем применении метода главных компонент происходит выделение факторов, обладающих меньшей дисперсией. На первоначальном этапе дисперсии всех факторов равны 1. поэтому общая дисперсия равна кол-ву переменных. Например,

Значение	Собств. зн-ие	% от общ. дисперсии
1	6,12	61,2
2	1,8	18
3	0,5	4,7
4	0,4	4
5	0,31	3,2
6	0,29	2,9
7	0,2	1,96
8	0,17	1,7
9	0,13	1,37
10	0,09	0,85

Во втором столбце находится дисперсия нового фактора, в третьем столбце - % от общей дисперсии для каждого фактора.

Первый фактор имеет 61,2% от общей дисперсии, второй – 18% и т.д.

Имеются некоторые рекомендации о том, сколько факторов нужно оставить, следование которым дает лучшие результаты на практике.

Критерий Кайзера

Оставляют факторы с общими значениями, большими 1.

В нашем примере оставляем 1-ый и 2-ой фактор.

Этот критерий является более употребимым.

Критерий каменистой осыпи.

Этот критерий является графическим. По нему собственные значения, представленные в таблице, наносятся на график.

Согласно этому критерию находят такое место на графике, с которого убывание собственных значений максимально замедляется.

В нашем примере это либо 2-ое либо 3-ье значение. Т.е. можно оставить либо 2 либо 3 фактора.

Известно, что критерий Кайзера иногда сохраняет слишком много факторов, в то время, как критерий каменистой осыпи сохраняет слишком мало факторов. Однако оба эти критерия хороши при нормальных условиях, когда имеется относительно небольшое число факторов и много переменных. На практике возникает вопрос, когда полученное решение может быть интерпретировано в рамках решаемой практической задачи. Поэтому на практике обычно получают несколько решений с большим или меньшим числом факторов, а затем выбирают наилучшее.