Лекции / 20

52.Критерий Вилкоксона и проверка гипотезы об однородности 2-ух выборок. Пример.

Данный критерий служит для проверки однородности 2-ух независимых выборок. Его достоинство в том, что он применим к СВ распределение которых неизвестно, они должны быть лишь непрерывны. Счит-ся, что если выборки однородны, то они извлечены из 1-ой ген. совокупноти и имеют одинаковые (неизвестные) ф-ции распределения F₁(x) и F₂(x), которые непрерывны.

Будем предполагать, что n₁<=n₂ (если это не так выборки меняют местами).

A: Проверка Н₀ в случае, если объем выборки не превосходит 25:

Правило1: пусть ; Н₀: F₁(x) =F₂(x); Н_а: F₁(x) ≠ F₂(x), тогда, чтобы проверить Н₀ надо:

1) варианты обеих выборок располагается в возраст. порядке. Наблюдаемое значение критерия W_набл. есть сумма порядковых номеров вариант 1-ой выборки;

2) находится по табл. критических точек нижняя критическая точка (критерий Вилкоксона) W_н.кр..

3) Находится верхняя критич. точка

W_в.кр .

Если W_набл.<W_н.кр. или W_набл.>W_в.кр., то Н₀ отвергают, в противном случае нет оснований ее отклонить.

Пример:

При уровне значимости, т.е. Q=0,025. Проверить об однородности двух выборок объемов n₁, n_2:

: 15 23 25 26 28 29

: 12 14 18 20 22 24 27 30

Расположим эл-ты обеих выборок в виде вариационного ряда и перенумеруем их

12	14	15	18	20	22	23	24	25	26	27	28	29	30	Варианты
1	2	3	4	5	6	7	8	9	10	11	12	13	14	Порядковые номера

Найдем наблюдаемое значение критерия Вилкоксона –– сумму порядковых номеров (они набраны курсивом) вариант первой выборки:

;

По таблице находим нижнюю критическую точку:

;

Найдем верхнюю критическую точку:

;

Т. к. 29<54<61, т. е. W_набл.<W_в.кр. нет оснований отклонить .

Правило2: пусть ; Н₀: F₁(x) =F₂(x); Н_а: F₁(x) > F₂(x).

Находим W_н.кр как и в правиле1. Если W_набл.>W_н.кр, то нет оснований отвергнуть Н₀.

Правило3: пусть ; Н₀: F₁(x) =F₂(x); Н_а: F₁(x) < F₂(x).

Находим W_набл. и W_в.кр . Если W_н.кр < W_набл.<W_в.кр, то нет оснований отклонить Н₀

Замеч-е: если несколько вариант только одной выборки одинаковы, то в общем вариационном ряду или приписывают обычные номера, т.е. совпадающие варианты нумеруются так, как если бы они были различным числами. Если же совпадающие варианты разных выборок, то всем им приписывают один и тот же порядок номер равный среднему арифметическому порядковых номеров, которые имели бы эти варианты до совпадения.

B. Проверка гипотезы при n>25, хотя бы для одной выборки.

1. пусть Н_а: F₁(x) ≠ F₂(x), находим 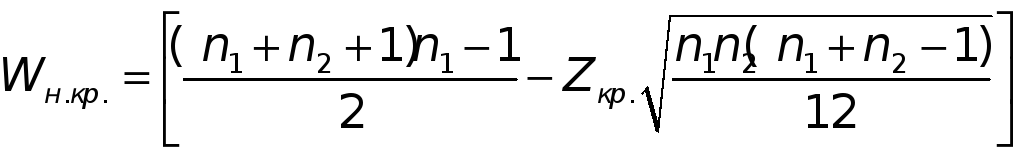(1)

Находим Z_кр. из условия , по табл. ф-ции Лапласа. [] в (1) означает целую часть. В остальном, правило тоже, что и в пункте А.

2. при Н_а: F₁(x) > F₂(x) или Н_а: F₁(x) < F₂(x)

W_н.кр находятся по ф-ле (1), Z_кр находим из .

В остальном, правило тоже, что и в пункте А., правила 2,3.