
Лекции / 23
.docВопрос 23.
Линейная регрессия. Корреляционное поле. Теоретические уравнения регрессии. Эмпирические уравнения регрессии. Коэффициэнты регрессии. Оценка корреляционной связи между СВ.Проверка гипотезы о согласованности линейного уравнения регрессии с экспериментальными данными.
Предположим, что
произведён эксперимент, в результате
которого получено n
значений СВ X
и
Y,
т. е. получен набор точек
![]() ,
i
= от 1 до n.
Нанесём эти точки на плоскость и получим
точечную диаграмму, которая наз.
корреляционным
полем. Если
точки на плоскости группируются около
прямой линии, то уравнение регрессии Y
на X
принимает вид:
,
i
= от 1 до n.
Нанесём эти точки на плоскость и получим
точечную диаграмму, которая наз.
корреляционным
полем. Если
точки на плоскости группируются около
прямой линии, то уравнение регрессии Y
на X
принимает вид:
![]() .
Это уравненіе наз. теоретическим
уравнением регрессии.
.
Это уравненіе наз. теоретическим
уравнением регрессии.
Требуется найти
коэффициэнты
![]() этого уравнения так, чтобы функция
этого уравнения так, чтобы функция
![]()
![]()
![]() т.е. принимала наименьшее значение. Эта
задача решается методом наименьших
квадратов. В результате его применения
для нахождения коэффициэнтов
т.е. принимала наименьшее значение. Эта
задача решается методом наименьших
квадратов. В результате его применения
для нахождения коэффициэнтов
![]() получаем систему:
получаем систему:
![]()
![]()
Введём обозначения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Система принимает вид:
![]()
![]() .
.
Коэффициэнт
![]() наз. коэффициэнтом
регрессии Y
на
X.
наз. коэффициэнтом
регрессии Y
на
X.
Аналогично выводится
теоретическое уравнение регрессии
X
на Y:
![]() ,
в котором коэффициэнт
,
в котором коэффициэнт
![]() наз. коэффициэнтом
регрессии X
наY.
наз. коэффициэнтом
регрессии X
наY.
Уравнение регрессии можно записать в виде:
![]()
![]()
![]() - коэффициэнты
регрессии Y
на X
и X
наY.
- коэффициэнты
регрессии Y
на X
и X
наY.
Тесноту корреляционной
связи между СВ X
и
Y
определяют с помощью корреляционного
отношения
![]() и
и
![]() .
ции
енками явл. эмпирический ции эффициэнтов
м ниуравнение регрессии
.
ции
енками явл. эмпирический ции эффициэнтов
м ниуравнение регрессии
![]()
![]() .
.
Свойства:
-
Если СВ X и Y связаны линейной зависимостью (коэффициэнты регрессии
 ),
то коэффициэнт корреляции = 1, если
),
то коэффициэнт корреляции = 1, если
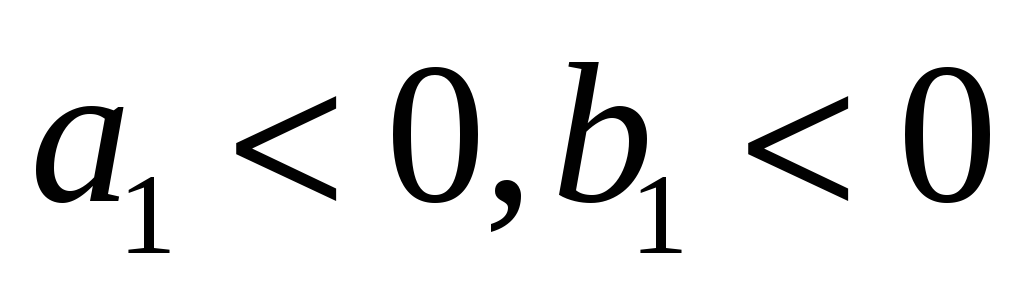 ,
то
,
то
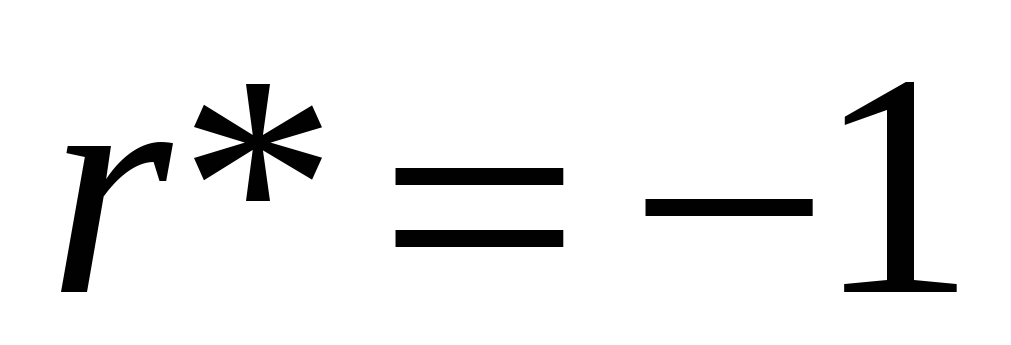 .
. -
При отсутствии лин. зависимости между X и Y линия регрессии параллельна коорд. осям, а коэфф. корреляции =0.
-
Во всех остальных случаях
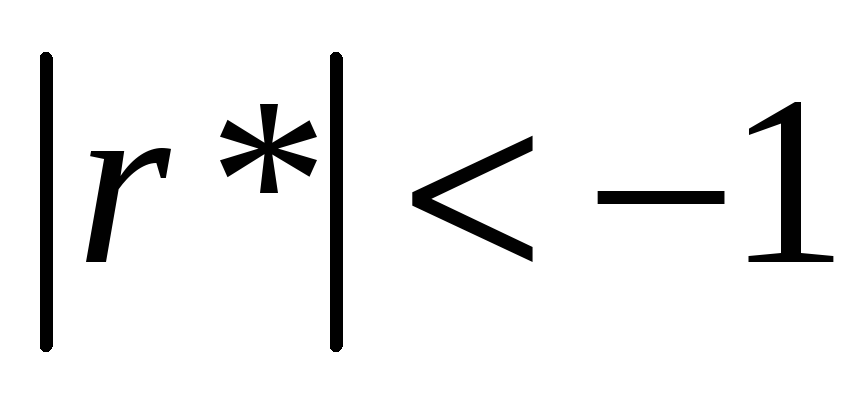 .
.
Т. о. чем ближе
коэф. корреляции по модулю к 1, тем теснее
лин. зависимость между X
и
Y.
Чем ближе он к нулю, тем эта зависимость
слабее. Однако может оказаться, что при
![]() ,
между X
и
Y
существует не линейная связь.
,
между X
и
Y
существует не линейная связь.
проверка гипотезы о согласованности линейного уравнения регрессии с экспериментальными данными.
Коэф.
![]() явл. точечными оценками теоретического
или модельного ур-я регрессии :
явл. точечными оценками теоретического
или модельного ур-я регрессии :
![]()
Для того чтобы выяснить хорошо ли найдены эти точечные оценки поступают след. образом:
-
Вычисляют остатки
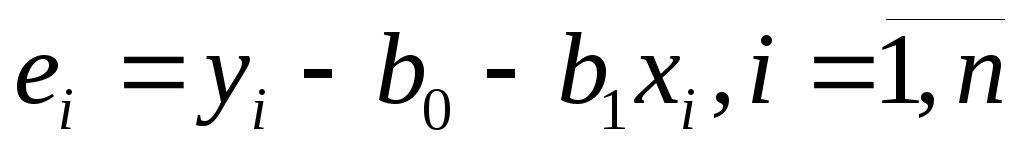
-
Вычисляют средние квадр. отклонения остатков характеризующих рассеяние эксперимент. точек относ. эмпир. линии регрессии
 ,
n-количество
точек
,
n-количество
точек -
Вычисляют среднее квадр. отклонение коэффициентов регрессии
 ,
,
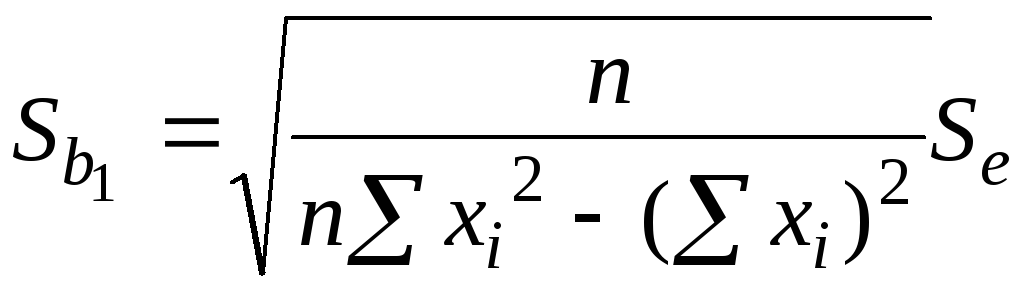
-
Находят интервальные оценки коэф-тов
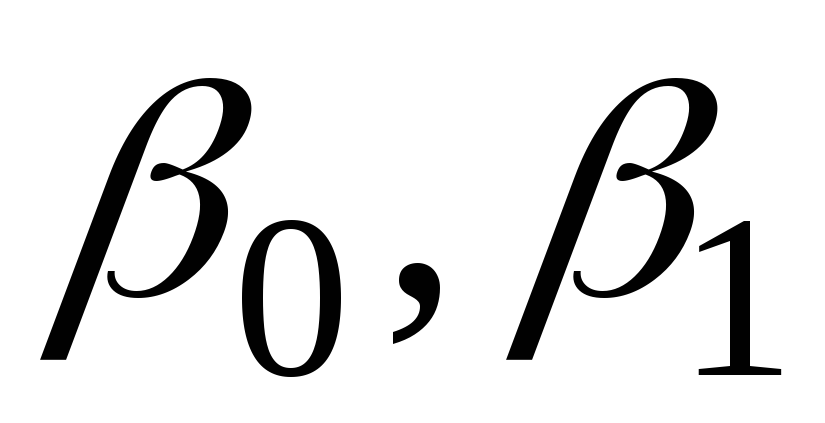 модельного ур-я регрессии
модельного ур-я регрессии
![]() ,
,
![]() ,
,
где
![]() -
коэфф-ты Стьюдента.
-
коэфф-ты Стьюдента.
-
Находят эмпирический коэф-т корреляции
 .
Квадрат эмпирич. коэф. корреляции
.
Квадрат эмпирич. коэф. корреляции
 наз.
коэф-том
детерминации
наз.
коэф-том
детерминации
Коэ-т детерминации
показывает процентное рассеяние точек
![]() объясняемое лин. регрессией Y
на X
(или X
на Y)
объясняемое лин. регрессией Y
на X
(или X
на Y)
Если
![]() =1,
то между СВ X,
Y
сущ. функциональная лин.связь.
=1,
то между СВ X,
Y
сущ. функциональная лин.связь.
Если напр.,
![]() =0,6,
то 60% рассеяния объясняется лин.
регрессией, а 40% остаются необъяснимыми.
=0,6,
то 60% рассеяния объясняется лин.
регрессией, а 40% остаются необъяснимыми.
-
Окончательное решение об адекватности лин. регрессии экспериментальным данным принимается на основании критерия Стьюдента
 ,
,
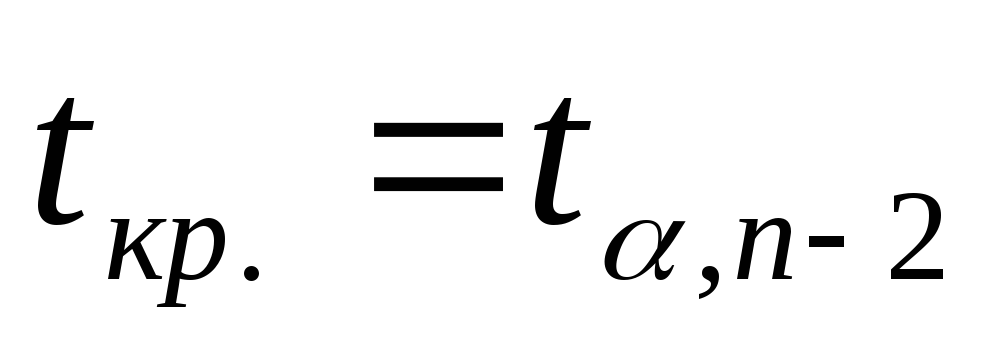
![]() -
уровень значимости
-
уровень значимости
Если
![]() ,
то лин. регрессия модельной ф-ции
,
то лин. регрессия модельной ф-ции
![]() выбрано удачно, т.е. согласуется с
экспериментальными данными;
выбрано удачно, т.е. согласуется с
экспериментальными данными;
Если
![]() ,
то модельная ф-я подобрана плохо, т.е.
не согласуется с данными эксперимента.
,
то модельная ф-я подобрана плохо, т.е.
не согласуется с данными эксперимента.
Замечание:
доказано, что если точки
![]() (
возможные значения СВ (X,Y))
расположены вдоль прямой, то СВ (X,Y)
распределена нормально.
(
возможные значения СВ (X,Y))
расположены вдоль прямой, то СВ (X,Y)
распределена нормально.
