4.1.2 Определение силы аэродинамического сопротивления движению кабины и противовеса

В скоростных лифтах возникают существенные по величине силы аэродинамического сопротивления, зависящие от аэродинамического качества и скорости движущихся частей.

Сила аэродинамического сопротивления движению кабины и противовеса:

F = c ∙A∙B∙ V²/2 ∙ ρ ∙ 10 ^–3, (кН) (1.9)

где с – коэффициент аэродинамического сопротивления обтеканию движущегося объекта (с=0.8÷1.2) в зависимости от конструкции объекта и наличия обтекателя для улучшения аэродинамического качества кабины; А, В – поперечные раз меры кабины (противовеса), м; V – скорость установившегося движения, м/с; ρ – плотность воздушного потока, кГ/м³ (ρ = 1.1÷1.125) кг/м³.

F = 1 ∙ 1,69 ∙ 0,71²/2 ∙ 1,1 ∙ 10 ^–3 = 0,0004 (кН)

Рассмотрим расчет более подробно с учетом расчетных схем, приведенных на рисунок 1.1.

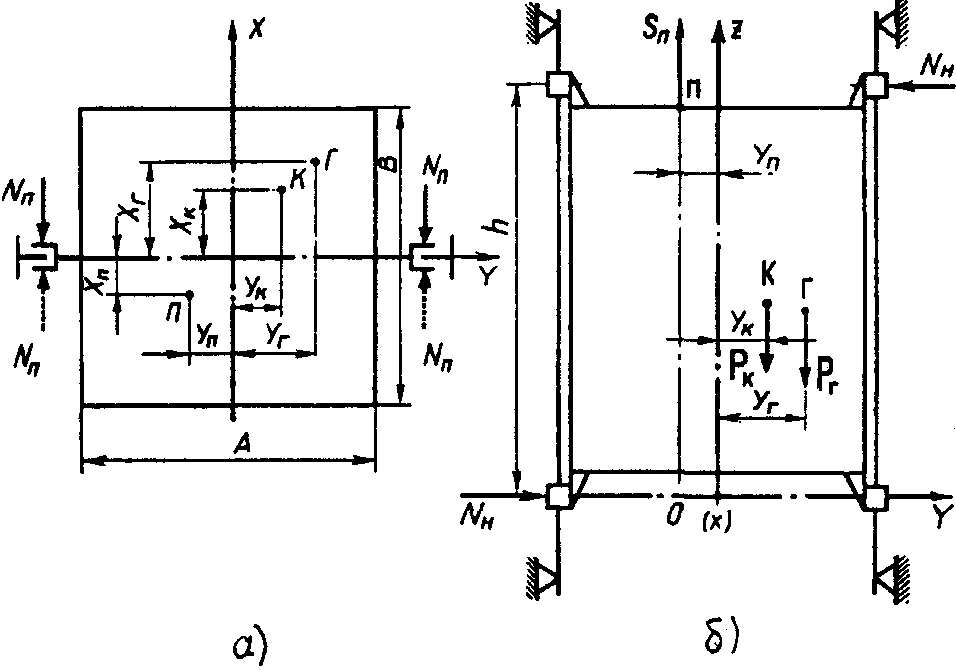
Рисунок 1.1 – Схемы к расчету опорных реакций башмаков кабины:

а) схема горизонтальной проекции кабины;

б) схема вертикальной проекции кабины

Приняты следующие обозначения:

А, В – ширина и глубина кабины, м; h – расстояние между башмаками по вертикали, м; П – обозначение точки подвески кабины; X_п, Y_п – продольное и поперечное смещение точки подвески кабины относительно центра пола, м; S_П – натяжение тяговых канатов, кН; К – положение центра масс кабины; Г – положение центра масс расчетного груза; X_К, Y_К – продольное и поперечное смещение центра масс кабины относительно центра пола, м; X_Г, Y_Г – продольное и поперечное смещение центра масс расчетного груза, м; N_П, N_Н – нормальные реакции в зоне контакта башмаков с направляющими, которые действуют перпендикулярно и параллельно плоскости направляющих; Р_К, Р_Г – сила тяжести кабины и груза, соответственно, кН.

Силы нормального давления, действующие на башмаки в плоскости направляющих и в перпендикулярном к ним направлении, определим из уравнений равновесия кабины:

∑ М_х = 0, ∑ М_у = 0 (1.10)

Из уравнений равновесия определим соответствующие нормальные реакции:

Nн = (Рг ∙ (Yг + Yп) + Рк ∙ (Yк + Yп))/h, (Н) (1.11)

Nп = (Рг ∙ (Xг + Xп) + Рк ∙ (Xк + Xп))/2h, (Н) (1.12)

где Р_г = Q_p·10 ^–2 – величина силы тяжести массы расчетного груза, кН (для пассажирского лифта Q_р=0.5·Q_c, где Q_c – грузоподъемность); Р_к – сила тяжести массы кабины, кН; X_п, Y_п – координаты смещения точки подвески кабины принимаются по конструктивным соображениям от 0.03 до 0.1 м; Х_К, Y_К – величина продольного и поперечного смещения центра масс кабины, зависящая от конструкции дверей кабины и может приниматься в пределах от 0,02 до 0,1 м; Х_Г=В/6; Y_Г=A/6 – определяются в предположении, что расчетный груз равномерно распределен по треугольной площадке, составляющей 50 % площади пола кабины, отделенной диагональю прямоугольного контура.

Nн = (2,5 ∙ (0,22 + 0,08) + 12,3 ∙ (0,06 + 0,08))/2,6 = 0,586 (Н)

Nп = (2,5 ∙ (0,22 + 0,08) + 12,3∙ (0,08 + 0,08))/2 ∙ 2,6 = 3,533 (Н)

Нормальные давления для кабины без груза:

Nнк = (Рк ∙ (Yк + Yп))/h, (Н) (1.13)

Nпк = (Рк ∙ (Xк + Xп))/2h, (Н) (1.14)

Nнк = (12,3 ∙ (0,06 + 0,08))/2,6 = 0,666 (Н)

Nпк = (12,3 ∙ (0,08 + 0,08))/2 ∙ 2,6 = 2,55 (Н)

Нормальные давления для расчетного груза без учета массы кабины:

Nнг = (Рг ∙ (Yг + Yп))/h, (Н) (1.15)

Nпг = (Рг ∙ (Xг + Xп)/2h, (Н) (1.16)

Nнг = (2,5 ∙ (0,22 + 0,08))/ 2,6 = 0,288 (Н)

Nпг = (2,5 ∙ (0,22 + 0,08) / 2 ∙ 2,6 = 0,975 (Н)

Сопротивление движению кабины без груза:

(при башмаках скольжения)

Fк = (2 Nнк + 4 Nпк) ∙ ωc + 0.015 ∙ Q_к∙ 10¯³, (кН) (1.17)

где ω_с = 0,12 ^— коэффициент сопротивления движению башмаков скольжения;

Fк = (2 ∙ 0,666 + 4 ∙ 2,55) ∙ 0,12 + 0,015 ∙ 1225,2 ∙ 10^-3 = 1,569 (кН)

Сила сопротивления движению расчетного груза:

(при башмаках скольжения)

Fг = (2 Nнг + 4 Nпг) ∙ ωc, (кН) (1.18)

Fг = (2 ∙ 0,288 + 4 ∙ 0,975) ∙ 0,12 = 0,537 (кН)

Сила сопротивления движению противовеса:

(при башмаках скольжения)

Fп = 7.5 ∙ Q_п ∙ 10¯⁵, (кН) (1.19)

Fп = 7,5 ∙ 1450,25∙ 10^-5 = 0,109 (кН)