Тема №8

Вариационный анализ

Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц совокупности в один и тот же период или момент времени.

Причиной вариации являются разные условия существования разных единиц совокупности. Вариация присуща всем без исключения явлениям природы и общества, кроме законодательно закрепленных нормативных значений отдельных социальных признаков.

Порядок проведения вариационного анализа:

1. Ряд распределения изображается графически. Для дискретного и ранжированного ряда – в виде полигона, для интервального – в виде гистограммы распределения.

На графике по оси абсцисс (х) откладываются значения группировочного варьирующего признака (х_i) или интервалы (для интервального ряда распределения). По оси ординат (f) соответствующие значения частот (f_i). При построении полигона распределения точки соединяются последовательно. При построении гистограммы – последовательно формируются столбцы, отражающие сочетание варьирующего признака с частотой в каждой группе (интервале) в отдельности.

В непрерывном интервальном ряду конечная величина одного интервала совпадает с начальным значением следующего за ним интервала.

Полигон распределения Гистограмма распределения

f_i f_i

f_n f_n

. .

. .

. .

f₂ f₂

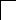f₁ f₁

х₁ x₂ … x_n x_i х_1н х_2н … x_nн х_nк x_ij

х_1к х_n-1к

Исходные данные для построения полигона или гистограммы распределения отражаются в таблице (табл.1 и 2 соответственно):

Таблица 1* Таблица2*

Величина варьирующего признака, xi	Частота, fi		Распределение варьирующего признака по группам, xij	Частота, fi
x1 x2 . . . xn	f1 f2 . . . fn		x1н – x1к x2н – x2к . . . xnн – xnк	f1 f2 . . . fn

*Во всех таблицах и расчетах варьирующий признак ранжируется в порядке возрастания.

В заключении делается предварительный вывод об общем характере распределения (о близости распределения к нормальному), в частности о симметрии или асимметрии относительно оси, об остроте или тупизне вершины относительно кривой нормального распределения.

Русский математик Ляпунов А.М. (1857 – 1918) доказал, что нормальное распределение образуется, если на варьирующий признак влияет большое число факторов, ни один из которых не имеет преобладающего влияния.

Основные параметры кривой нормального распределения

где t – нормированное отклонение,

- индивидуальные значения признака,

- среднее значение признака,

М_о - мода распределения,

М_е - медиана распределения,

Q - квартильное отклонение,

- среднее квадратическое отклонение.

2. Рассчитывается средняя (типичная) величина варьирующего признака () по формуле средней арифметической взвешенной как отношение суммы произведений варьирующего признака (х_i) на соответствующую частоту (f_i) к сумме частот:

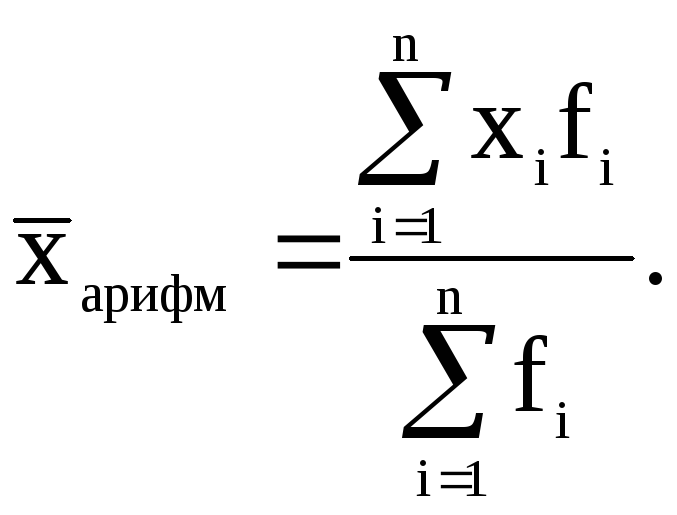
В интервальном ряду для расчета средней, а также всех последующих вычислений необходимо выявить середины интервалов (х_i). Для этого начальное значение интервала (х_н) складывают с его конечной величиной (х_к) и делят пополам (табл.3):

Таблица 3

Распределение варьирующего признака по группам, xij	Середина интервала, хi	Частота варьирующего признака, fi
x1н – x1к x2н – x2к . . . xnн – xnк	. . .	f1 f2 . . . fn

Для удобства и наглядности последующих расчетов необходимо оформить таблицу (табл.4, стр.4):