Достаточные условия локального экстремума. Достаточные условия экстремума функции двух переменных
Пусть в некоторой области, содержащей точку М0(х0,у0), функцияf(x,y) имеет непрерывные частные производные до второго порядка в точке М0(х0,у0) и некоторой её окрестности. Пусть, кроме того, пусть в этой точке М0(х0,у0) выполняются необходимые условия экстремума функцииf(x,y)
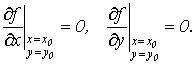(1)
Тогда функция f(x,y) в точке М0(х0,у0) имеет максимум, еслиВ2–А·С< 0,A< 0;
функция f(x,y) в точке М0(х0,у0) имеет минимум, еслиВ2–А·С< 0,A> 0;
функция f(x,y) в точке М0(х0,у0) не имеет ни максимума, ни минимума, еслиВ2–А·С> 0;
функция f(x,y) в точке М0(х0,у0) может иметь, и может не иметь экстремум (в этом случае требуются дополнительные исследования), еслиВ2–А·С= 0;
где
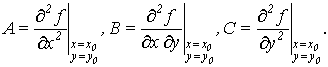
Представим приращение функции по формуле Тейлора в виде
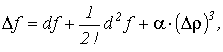(2)
где
Так
как для функцииf(x,y) в точке
М0(х0,у0)
выполнены соотношения (1), то (2) можно
представить в виде
(3)
Для достаточно малого Δρ знак левой части соотношения (3) будет совпадать с d2f
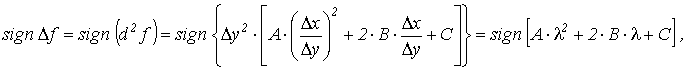
где
,
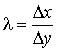Δу ≠ 0.
Исследование квадратичной формы для функции двух переменных. Метод вычисления критериев Сильвестера.
Применение критерия Сильвестера для определения экстремума функции многих переменных требует вычисления определителей порядка. Рассмотрим один из возможных методов диагонализации матриц и соответственно получения треугольных определителей.Метод основан на последовательном понижении порядка определителя. При этом :
1.На каждом этапе понижения порядка определителя, удобная для применения вычислительной техники.
2.Получаемые в результате диагональные элементыопределителей являются элементами критерия Сильвестера и позволяют, так сказать, в “ходе вычисления” вести контроль знакоопределенности квадратичной формы.
В основу алгоритма вычислений положины два свойства определителей.
1.Известно, что
a 11 a 12
a 21 a 22
Впредь замена любого определителя второго порядка элементом a 11 назовем “сверткой” определителя.
2.Определитель порядка не изменится, если элементы какой-либо строки умножить (разделить) на какое-либо число, не равное нулю, и сложить (вычесть) с элементами другой строки.
Итак, рассмотрим определитель n-го порядка, составленный из вторых частных производных некоторой функции n– переменных f(x 1 ,x2 ,…,xn ).
Положим a ik = fxixk ’’ .Имеем
a 11 a 12 … a 1n
………………… (5.9)
a n1 a n2 … a nn
Умножим в (5.9) элементы первой строки на a 21/ a11 и вычтем их из элементов второй строки.
Умножим в (5.9) элементы первой строки на a 31/ a11 и вычтем их из элементов третьей строки. …
Умножим в (5.9) элементы первой строки на a n1/ a11 и вычтем их из элементов последней строки.
Выполнив последовательно эти операции, получим
a 11 a 12 … a 1n
0 a 22 - a 12 a 21/ a 11 … a 2n -a 1n a n1/ a 11
……………………………………………………… (5.10)
0 a n2 - a 12 a n1/ a 11 … a nn - a 1n a n1/ a 11
Умножим каждую строку в (5.10), начиная со второй на a 11 ,при этом определитель (5.10) умножится на a11 n-2
1
----------- (5.11)
a 11 n-2
где
a 11 a 22 - a 12 a 21 a 11 a 23 - a 13 a 21 … a 11 a 2n - a 1n a 21
a 11 a 32 - a 12 a 31 a 11 a 33 - a 13 a 31 … a 11 a 13n - a 1n a 31
………………………………………………… (5.12)
a 11 a n2 - a 12 a n1 a 11 a n3 - a 13 a n1 … a 11 a nn - a 1n a n1
Рассмотрим более внимательно элементы (5.12). Перепишем (5.12) в виде
a 11 a 12 … a 1n-1
a 21 a 22 … a 2n-1
………………… (5.13)
a n-11 a n-12 … a n-1n-1
Из сравнения (5.12) и(5.13) видно, что
a 11 – есть свертка определителя a11 a12
a 21 a22
a 12 – есть свертка определителя a11 a13
a 21 a23
…………………………………………………..
a 1n-1 – есть свертка определителя a11 a1n
a 21 a2n
.
Таким образом, первая строка 1n-1 является сверткой элементов первых двух строк определителяn . Более наглядно это можно сфрмклировать так : последовательно каждый “прямоугольник” элементов первой и второй строк заменяется его сверткой ; причем первые элементы двух строк “участвуют” во всех прямоугольниках этих строк.
a 11 a 12 a 13 … a 1n
a 11 a 12 a 1n-1
a 21 a 22 a 23 … a 2n
Аналогично вторая строка определителя n-1 является сверткой элементов первой и третьей строк исходного определителя.
a 11 a 12 a 13 … a 1n
a 21 a 22 a 2n-1
a 31 a 32 a 33 … a 3n
Наконец для последней строки n-1 имеем
a 11 a 12 a 13 … a 1n
a n-1 1 a n-1 2 a n-1n-1
a n1 an2 an3 … ann
Если теперь применить те же опервции к определителю n-1 , т. е. к (5.13), получим
1
……
a 11 n-3 (5.14)
где
a 11 a12 … a1 n-2
a 21 a22 … a2 n-2
……………………………..
a n-2 1 a n-2 2 … a n-2 n-2
а элементы a ik являются сверткой соответствующих определителей – прямоугольников.
Очевидно, повторяя эту операцию n–1 раз, получим следующую формулу, предварительно введя более простые обозначения :
a 11 = a1 – левый угловой верхний элемент
a 11 = a2 – левый угловой верхний элемент
a 11 = a3 – левый угловой верхний элемент
…………………………………………
a 11 = an – левый угловой верхний элемент.
С учетом этого
a n
………………………..
a 1 n-2 a2 n-3 … an-1 (5.15) n>2