
- •3. Дифференциальное исчисление функций нескольких переменных.
- •Принцип выбора Больцано-Вейштрасса. Распространение на случай пространства произвольной конечной размерности
- •Предел функции. Повторные пределы функции. Предел функции нескольких переменных
- •Определение
- •Равенство повторных пределов
- •Критерий Коши существования предела функции.
- •Непрерывность функции по совокупности переменных и по каждой переменной в отдельности.
- •Непрерывность и суперпозиция непрерывных функций.
- •2. Непрерывность сложной функции.
- •Теорема Коши о промежуточном значении функции, непрерывной на множестве.
- •Теорема Вейерштрасса о функциях, непрерывных на множествах. Теорема Вейерштрасса для непрерывных функций на компакте
- •Равномерная непрерывность функции нескольких переменных. Теорема Кантора.
- •Доказательство. Воспользуемся доказательством от противного.
- •Замечания
- •Частные производные от функции нескольких переменных.
- •Формула для полного приращения функции. Дифференцируемость функции в точке.
- •Функции нескольких переменных
- •Теорема о дифференцируемости сложной функции.
- •Связь между полным дифференциалом и полным приращением функции. Дифференциал функции
- •Связь дифференциала с частными производными
- •Инвариантность формы первого дифференциала.
- •Касательная плоскость и нормаль к поверхности.
- •Производная от скалярной функции по данному направлению.
- •Градиент скалярной функции и его аналитическое выражение. Оператор «набла».
- •Определение
- •Частные производные высших порядков. Теорема о независимости смешанной производной от порядка дифференцирования. Частные производные высших порядков
- •Основа теоремы о независимости смешанной производной от порядка дифференцирования
- •Полные дифференциалы высших порядков. Дифференциал высшего порядка функции нескольких переменных
- •Формула Тейлора для функции нескольких переменных.
- •Понятие неявной функции. Теорема о её существовании и дифференцируемости. Неявно заданная функция
- •Теорема существования и дифференцируемости функции, заданной неявно
- •Вычисление частных производных функция, заданных неявно.
- •Необходимые условия локального экстремума функции нескольких переменных. Локальный экстремум функций нескольких переменных. Необходимые условия безусловного локального экстремума.
- •Необходимые условия экстремума функции многих переменных.
- •Достаточные условия локального экстремума. Достаточные условия экстремума функции двух переменных
- •Исследование квадратичной формы для функции двух переменных. Метод вычисления критериев Сильвестера.
- •Понятие условного экстремума. Сведение условного экстремума к безусловному.
- •Метод неопределённых множителей Лагранжа.
- •Описание метода
- •Обоснование
- •Двумерный случай
Частные производные высших порядков. Теорема о независимости смешанной производной от порядка дифференцирования. Частные производные высших порядков
Пусть
задана функция f(x, y). Тогда каждая
из ее частных производных(если они,
конечно, существуют)![]() и
и![]() ,
которые называются такжечастными
производными первого порядка, снова
являются функцией независимых переменныхx, yи может, следовательно также
иметь частные производные. Частная
производная
,
которые называются такжечастными
производными первого порядка, снова
являются функцией независимых переменныхx, yи может, следовательно также
иметь частные производные. Частная
производная обозначается
через
обозначается
через![]() или
или![]() ,
а
,
а через
через![]() или
или![]() .
Таким образом,
.
Таким образом,
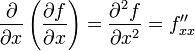 ,
,

и, аналогично,
 ,
,
 .
.
Производные
![]() и
и![]() называютсячастными производными второго порядка.
называютсячастными производными второго порядка.
Определение:
Частной производной второго порядка
от функции z=f(x;y) дифференцируемой в
области D,называется первая производная
от соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможные частные
производные третьего порядка:![]() ,
,![]() ,
,![]() и т. д.
и т. д.
Основа теоремы о независимости смешанной производной от порядка дифференцирования
Для достаточно гладкой функции многих переменных значение смешанной производной не зависит от порядка дифференцирования:
![]()
Идея доказательства в лекции (равенство путей дифференцирования).
Полные дифференциалы высших порядков. Дифференциал высшего порядка функции нескольких переменных
Если
функция
![]() имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так:
имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так:![]() .
.
![]()
![]()
![]()
![]()
Символически
общий вид дифференциала n-го порядка
от функции![]() выглядит
следующим образом:
выглядит
следующим образом:
![]()
где
![]() ,
а
,
а![]() произвольные
приращения независимых переменных
произвольные
приращения независимых переменных![]() .
Приращения
.
Приращения![]() рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа переменных
рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа переменных
Формула Тейлора для функции нескольких переменных.
Формула
Тейлора для функции нескольких переменных)
Пусть функция
![]() задана
в области
задана
в области![]() и
имеет в
и
имеет в![]() все
частные производные до порядка
все
частные производные до порядка![]() включительно.
Пусть
включительно.
Пусть![]() и
и![]() --
две точки области
--
две точки области![]() ,
такие что весь отрезок между ними целиком
лежит в
,
такие что весь отрезок между ними целиком
лежит в![]() .
Тогда для некоторой точки
.
Тогда для некоторой точки![]() этого
отрезка имеет место равенство
этого
отрезка имеет место равенство
|
|
(9.6*) |
|
|
|
|
|
|
|
|
(9.7) |
Сумма
всех слагаемых в правой части формулы
(9.6*),
кроме записанных в последней строке,
называется многочленом Тейлора функции![]() в
точке
в
точке![]() ,
а эта последняя строка содержит остаточный
член формулы Тейлора. Считая его малым
при небольших расстояниях между
,
а эта последняя строка содержит остаточный
член формулы Тейлора. Считая его малым
при небольших расстояниях между![]() и
и![]() (он
имеет порядок
(он
имеет порядок![]() ,
в то время как все остальные слагаемые --
порядок не выше
,
в то время как все остальные слагаемые --
порядок не выше![]() ,
если не обращаются в 0), мы можем не
учитывать остаточный член и, тем самым,
получаем приближённую формулу
,
если не обращаются в 0), мы можем не
учитывать остаточный член и, тем самым,
получаем приближённую формулу
|
|
|
|
|
|
|
|
|
содержащую
лишь значения функции
![]() и
её частных производных, вычисленные в
точке
и
её частных производных, вычисленные в
точке![]() (но
не в других точках
(но
не в других точках![]() ).
Эту формулу можно использовать для
приближённого вычисления значений
функции
).
Эту формулу можно использовать для
приближённого вычисления значений
функции![]() в
точках
в
точках![]() ,
близких к
,
близких к![]() .
На практике её применяют, ввиду большого
числа слагаемых в правой части, лишь
при небольших значениях
.
На практике её применяют, ввиду большого
числа слагаемых в правой части, лишь
при небольших значениях![]() ,
как правило,
,
как правило,![]() и
и![]() .
.
При
![]() получается
линейное приближение функции
получается
линейное приближение функции![]() (нетрудно
видеть, что правая часть совпадает с
линейной функцией
(нетрудно
видеть, что правая часть совпадает с
линейной функцией![]() ,
графиком которой служит касательная
плоскость, проведённая при
,
графиком которой служит касательная
плоскость, проведённая при![]() к
графику функции
к
графику функции![]() ):
):
|
|
|
При
![]() получается
квадратичное приближение функции
получается
квадратичное приближение функции![]() :
:
|
|
(9.8) |
Многочлен
Тейлора в этом случае оказывается
многочленом второй степени относительно
переменных
![]()









