32. Непрерывность функции по совокупности переменных и по каждой переменной в отдельности.

Определение 6. Функцияf (х, у) называется непрерывной в точке M₀(x₀,y₀), если она определена в точке и некоторой  её окрестности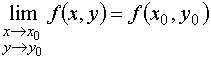 иили.

            Введём обозначения:

, ,,.

Определение 7. Функция f(x,y) непрерывна в точке (x₀,y₀), еслиили.

        Иначе говоря, функция z  = f (х, у) непрерывна в точке M₀(x₀,y₀), если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции.

Определение 8. Функция непрерывна в области D , если она непрерывна в каждой точке этой области. Точки, в которых условия непрерывности нарушены, называются точками разрыва(это точки, где функция не определена).

Определение 9. Точка M₀называется точкой разрыва функции u= f(M), если функция u= f(M) определена вблизи точки M₀(то есть её окрестности), но не определена в самой точке M₀. Линия, все точки которой являются точками разрыва   функции u= f(M) , называется линией разрыва этой функции.

32. Непрерывность и суперпозиция непрерывных функций.

1. Алгебраическая сумма и произведение конечного числа непрерывных в данной точке функций есть непрерывная функция в этой  точке. Частное двух непрерывных функций в точке, при условии, что знаменатель отличен от нуля в этой точке, также есть непрерывная функция в этой точке.

2. Непрерывность сложной функции.

            Пусть инепрерывны в некоторой точке

и пустьнепрерывна в  точке

пространства , соответствующей точкеP₀, тогда такая функция v будет непрерывна в точкеP₀.

3. Если  z=f(x,y)=f(M)   непрерывна в замкнутой области, то функция z :

                    1) ограничена в области ;

                    2) принимает в свои наименьшее и наибольшее значения;

                     3) если в двух точках А и В области D функция принимает неравные значения, то она принимает и всякое промежуточное  между ними значение по крайней мере в одной точке любой кривой, соединяющей точки А и В и целиком лежащей в области D . В частности, если f(A) и f(B) –  числа противоположных знаков, то функция f(M)   обращается в нуль по крайней мере в одной   точке любой упомянутой кривой;

32. Теорема Коши о промежуточном значении функции, непрерывной на множестве.

Если непрерывная функция принимает два значения, то она принимает и любое значение между ними.

32. Теорема Вейерштрасса о функциях, непрерывных на множествах. Теорема Вейерштрасса для непрерывных функций на компакте

Пусть дано топологическое пространство и компактное подмножество. Пусть дана непрерывная функция. Тогда

и

Компа́ктное простра́нство— определённый тип пространств, включающий:

- Все пространства с конечным числом точек;

- Все замкнутые и ограниченные подмножества евклидова пространства.

32. Равномерная непрерывность функции нескольких переменных. Теорема Кантора.

Равномерная непрерывность: при всякомнайдётся такое число, что для любых двух точек А и В области D, расстояние между которыми меньше, будет справедливо неравенство. Функция, непрерывная по совокупности аргументов, будет непрерывна и по каждому аргументу в отдельности (при фиксированных других аргументах). Обратное же неверно.

Теорема Кантора - Функция, непрерывная на компакте, равномерно непрерывна на нём.

Пусть даны два метрических пространства иПусть также дано компактное подмножествои определённая на нём непрерывная функцияТогдаравномерно непрерывна на

Доказательство. Воспользуемся доказательством от противного.

Пусть — функция, отвечающая условиям теоремы (на компакте), но не равномерно непрерывная на нём. Тогда существует такое, что для всехсуществуют такиеи, расстояние между которыми меньше, но расстояние между их образами не менее:

но

Возьмём последовательность , сходящуюся к 0, например,. Построим последовательностиитак, чтобы, но

—компакт, поэтому можно выделить сходящиеся последовательности:

Но так как расстояние между ними стремится к нулю, по лемме о вложенных отрезках они стремятся к одной точке: . И, так какнепрерывна, что противоречит предположению, что.

Стало быть, функция, непрерывная на компакте, действительно равномерно непрерывна на нём.