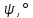ТАУ отчёт №12

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

ОТЧЁТ О ЛАБОРАТОРНОЙ РАБОТЕ №12

Дисциплина: Теория автоматического управления

Тема: Вынужденные колебания нелинейных систем

Вариант №3

Д.А. Киселёв Л.В. Бабко

Выполнил студент гр.4081/10

Преподаватель

Санкт-Петербург

2012

Цель работы:

Исследование условий синхронизации автоколебательных нелинейных систем внешним гармоническим воздействием.

Исследуемая схема:

Линейная часть системы имеет передаточную функцию W(p), а нелинейный элемент описывается комплексным коэффициентом W_Н(A).

Исходные данные:

T₁ = 0.2 с; T₂ = 0.1 с; T₃ = 0.1 с; K = 5

Нелинейный элемент:

c = 1

1. Расчёт автоколебаний на входе нелинейного элемента

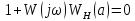
Выделим вещественную () и мнимую () части:

Частота автоколебаний:

Амплитуда автоколебаний:

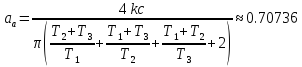
2. Исследование вынужденных колебаний

Пороговому значению амплитуды входных колебаний соответствует вектор на комплексной плоскости, перпендикулярный вещественной оси, который начинается в точке и заканчивается на вещественной оси, умноженный на .

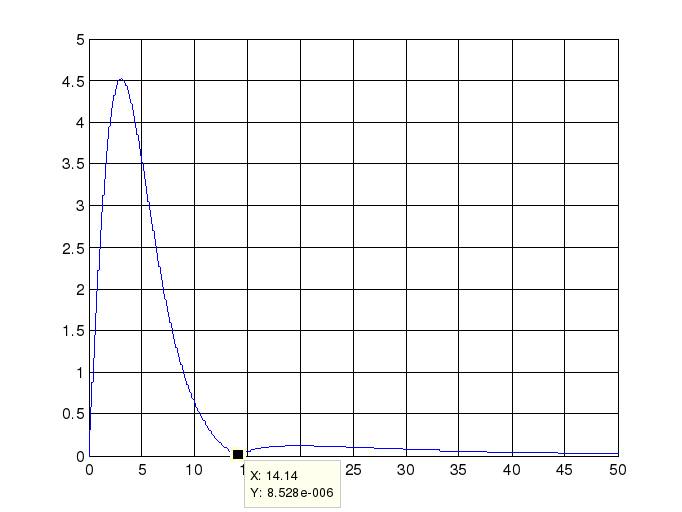
Зависимость порогового значения амплитуды от частоты внешнего гармонического сигнала построим с помощью Matlab:

T1=0.2; T2=0.1; T3=0.1; k=5;

w = 0:0.01:50;

W = k./(1+j*T1.*w)./(1+j*T2.*w)./(1+j*T3.*w);

figure

plot( w, abs(imag(W)).*4./pi )

grid on

Фазу вынужденных колебаний можно вычислить следующим образом:

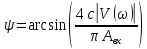
Зависимость фазы вынужденных колебаний от амплитуды внешнего гармонического сигнала при построим с помощью Matlab:

w = sqrt((T1+T2+T3)/(T1*T2*T3))/2;

W = k/(1+j*T1*w)/(1+j*T2*w)/(1+j*T3*w);

a = 0:0.01:20;

figure

plot( a, asin(4*c*abs(imag(W))/pi./a)./pi.*180 )

grid on

3. Схема моделирования в Simulink

В блоке Subsystem содержится линейная часть системы:

Амплитуда входного гармонического сигнала может устанавливаться с помощью блока Slider Gain. В блоке Transport Delay установлено время задержки 2 с.

4. Моделирование

Переходные процессы в системе при отсутствии входного сигнала:

На первом графике – входной сигнал, на втором – автоколебания на входе нелинейного элемента, на третьем – выходной сигнал. Амплитуда автоколебаний . Частота автоколебаний .

Переходные процессы в системе при входном сигнале с частотой и амплитудой :

При t от 0 до 2 входной сигнал отсутствует и на входе нелинейного элемента есть автоколебания. Затем появляется входной сигнал, и через 3 секунды (при t=5) на входе нелинейного элемента устанавливаются вынужденные колебания с амплитудой 1.467 и частотой 7.9534 рад/сек.

Промоделируем эти же переходные процессы до t=200, чтобы затем сравнить их с переходными процессами при . Переходные процессы в системе при входном сигнале с частотой и амплитудой :

Переходные процессы в системе при входном сигнале с частотой и амплитудой :

Здесь синхронизации с внешним источником не происходит, так как амплитуда внешнего сигнала для этого слишком мала.

При частоте входного сигнала минимальное значение 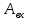, при котором происходит синхронизация системы, то есть , примерно равно 1.401.

Зависимость порогового значения амплитуды от частоты внешнего гармонического сигнала:

, рад/сек
4	5
8	1.401
12	0.19
16	0.09
20	0.2
24	0.3
28	0.376

Нанесем полученные точки на расчётную зависимость:

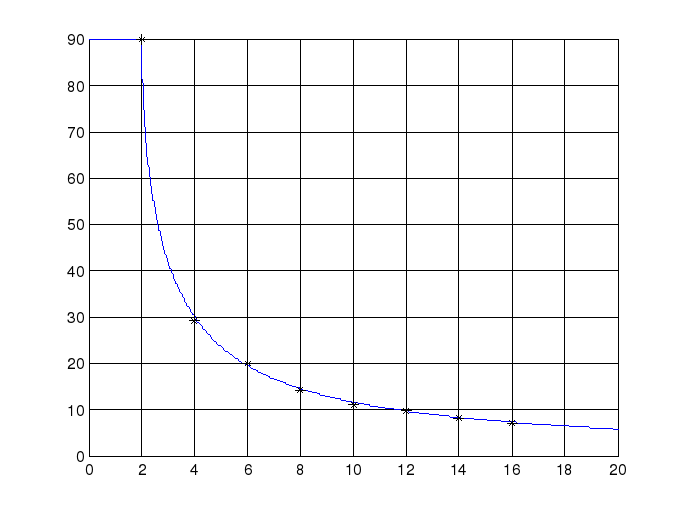
Зависимость фазы вынужденных колебаний от амплитуды внешнего гармонического сигнала при :

2	90
4	29
6	20
8	14
10	11
12	9.5
14	8
16	7

Нанесем полученные точки на расчётную зависимость:

5. Выводы

Рассчитанные теоретические зависимости подтверждены экспериментально. При частоте входного сигнала, совпадающей с частотой, на которой АФЧХ линейной части системы пересекает вещественную ось, возможна синхронизация колебаний системы с внешним источником при любом значении амплитуды внешнего сигнала. Фаза вынужденных колебаний уменьшается при увеличении амплитуды внешнего сигнала.