20.Алгоритм метода половинного деления.

1.Определить новое приближение корня х в середине отрезка [а,b]: х=(а+b)/2.

2.Найти значения функции в точках а и х: F(a) и F(x).

3.Проверить условие F(a)*F(x) < 0. Если условие выполнено, то корень расположен на отрезке [а,х]. В этом случае необходимо точку b переместить в точку х (b=х). Если условие не выполнено, то корень расположен на отрезке [х,b]. В этом случае необходимо точку а переместить в точку х (а=х).

4.Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм продолжить до того времени, пока не будет выполнено условие /F(x)/ < e (заданная точность).

21.Метод простой итерации для поиска корней. Геометрическая интерпретация.

Исходное уравнение f(x)=0 эквивалентными преобразованиями приводится к виду с выделением неизвестного в левой части, то есть x=φ(x), где φ(x) – некоторая функция, связанная с исходной функцией f(x). Такая форма записи уравнения позволяет, задаваясь начальным приближением x_0, получить следующее, первое приближение x₁=φ(x₀), далее получают второе приближение x₂=φ(x₁) и так далее x_n+1=φ(x_n)…. Последовательность {x_n}= x_0, x_1, x_2, …, x_n,… называется последовательностью итераций или приближений с начальным значением x_0. Если функция φ(x) на [a,b] непрерывна и существует предел ξ = lim x_n при n→∞, то, переходя к пределу в равенстве x_n+1=φ(x_n), найдем, что при n→ ∞: lim x_n+1=lim φ(x_n)=φ(lim x_n), то есть ξ=φ(ξ). Следовательно, если последовательность приближений сходится, то она сходится к корню уравнения (2), а значит и уравнения (1). В силу сходимости итерационного процесса этот корень можно вычислить при достаточно большом n с любой заданной точностью. Однако необходимо определить при каких условиях последовательность {x_n}будет сходящейся. Получим связь между погрешностями двух соседних приближений - ε_n и ε _n+1: x_n=ξ+ε_n, x_n+1=ξ+ε _n+1. Подставим эти представления в x_n+1=φ(x_n) и разложим функцию в ряд Тейлора в окрестности корня: ξ+ε_n+1=φ(ξ+ε_n)=φ(ξ)+ε_nφ’(ξ)+(ε_n²/2!)φ’’(η), где η  [ξ; ξ+ε_n]  [a;b]. Поскольку ξ - корень, то ξ=φ(ξ)_, то получаем: ε_n+1=ε_n φ’(ξ)+(φ’’(η)/2)ε_n². Так как ε<1, то ε_n²<<ε_{n .} Поэтому если φ’(ξ)  0,то основной вклад в погрешность дает первое слагаемое, а слагаемым (φ’’(η)/2)ε_n² можно пренебречь, то есть ε_{n+1 } ε_n φ’(ξ). Это означает, что погрешность будет уменьшаться на каждом последующем шаге, если |φ’(ξ)|<1, тогда для любого n |ε_n+1|<|ε_n|. Сформулируем теорему о сходимости метода простых итераций, дающую достаточные условия сходимости.

Теорема о сходимости метода простых итераций. Пусть ξ - корень уравнения x=φ(x), функция φ(x) определена и дифференцируема на отрезке [a,b], причем для x [a,b] все значения функции φ (x)  [a,b]. Тогда, если существует такое положительное число q<1, что при x  [a,b] выполняется неравенство |φ’(ξ)|≤q<1, то на отрезке [a,b] уравнение x=φ(x) имеет единственный корень x=ξ и процесс итераций, выраженный формулой x_n+1=φ(x_n), где n=1,2,3… , сходится к этому корню независимо от выбора начального приближения x₀  [a,b]. Таким образом, последовательность {x_n},начинающаяся с любого x₀  [a;b], сходится к корню ξ со скоростью геометрической прогрессии, причем скорость сходимости тем выше, чем меньше величина q  (1;0). Если функция φ(х) монотонно возрастает и 0<φ’(х)<1, то все приближения лежат по одну сторону от корня - такую сходимость называют монотонной (или ступенчатой) – рис.1. Если функция φ(х) монотонно убывает и 0>φ’(х)>-1, то соседние приближения лежат по разную сторону от корня – такую сходимость называют двусторонней (или спиралевидной) – рис.2. Поскольку в этом случае корень заключен в интервале, концами которого являются соседние приближения – ξ(x_n,x_n+1), то выполнение условия |x_n+1-x_n|<ε обеспечивает выполнение условия |ξ-x _n+1|<ε.

Чтобы можно было сравнивать итерационные методы по скорости сходимости, вводят следующие понятия:

Определение 1: Сходимость последовательности {x_n} к ξ называется линейной (соответственно, итерационный процесс - линейно сходящимся), если существует такая постоянная C(0,1) и такой номер n₀, что выполняются неравенства |ξ-x_n+1|≤C|ξ-x_n| для n≥n_0.

Для введенных ранее погрешностей это означает |ε _n+1|≤C|ε_n|. В методе простой итерации в роли постоянной C выступает значение q, то есть метод сходится линейно.

Определение 2: Последовательность приближений {x_n} сходится к ξ по меньшей мере с р-ым порядком (соответственно, итерационный процесс имеет по меньшей мере p-ый порядок), если найдутся такие константы C>0, p≥1 и n₀, что для всех n≥n₀ выполняются условия |ξ-x_n+1|≤C|ξ-x_n |^р (или в других обозначениях |ε _n+1|≤C|ε_n|^p).

22. Приведение уравнения к виду, пригодному для применения метода итераций.

f(x)=0

f’(x)=0, если f’(x)<0, то рассматриваем ур-я –f(x)=0

m=min f’(x)=<f’(x)=<max f’(x)=M для всех x c [a;b]

умножим исходное уравнение f(x)=0 на λ>0 и добавим по x в каждую часть, так чтобы был вид x=x- λf(x) => ϕ(x)=x- λf(x)

ϕ’(x)=1- λf’(x) потребуем, чтобы 0=< ϕ’(x)<1 , если условие выполнено, то x=x-λf(x) – сходит. получаем 2 соотношения: 0=<1-λf’(x)<1

λf’(x)=<1 и λf’(x) >0 возьмем за λ =1/M, чтобы для любого x промежутка выполнялось λf’(x)=<1

1-(1/M)*f’(x) --> max=1-m/M<1 , следовательно метод итер. будет сходится.

23.Общая оценка погрешности приближения к корню.

Теорема о погрешности приближенного решения

Пусть ξ―точный корень, а х*―приближенный корень уравнения f(x)=0, принадлежащие одному и тому же отрезку [a,b]. Если f(x) определена и непрерывна на [a,b] и для всех x[a,b] выполняется неравенство │f '(x)│≥m>0, то справедлива оценка

|х*-ξ|≤│f(x*)│/m,

где m−наименьшее значение модуля производной f '(x) на [a,b]. Доказательство. Применим теорему Лагранжа о конечных приращениях (теорему о среднем значении): если функция f(x) определена и непрерывна на отрезке [x*,ξ] и имеет конечную производную в интервале (x*,ξ), то внутри (x*,ξ) найдется хлтя бы одна такая точка , для которой

f(x*)-f(ξ)=f '(η)•(x*-ξ), x*≤η≤ξ .

Отсюда получим │х*-ξ│=│f(x*)│∕│f '(η)│≤││ или │х*-ξ│≤││.

Теорема доказана. Суть полученной оценки в том, что само значение f(x*) не в полной мере характеризует степень близости х* к корню, следует учитывать также наклон кривой в окрестности приближения. Если производная в этой окрестности достаточно мала, то можно недооценить х*, что иллюстрируется на рис. 5.

Хотя значение f(x*) меньше заданного малого числа , величина х* еще далека от точного значения корня .

24.Оценка погрешности приближения в методе простой итерации.

Виды погрешности: 1. неустранимая погрешность или погрешность исходной информации (сумма погрешности математической модели и погрешности исходных данных),2.погрешность метода или погрешность аппроксимации (порождается применяемым приближенным методом решения)3.вычислительная погрешность или погрешность округления (результат конечности разрядной сетки сумматора). Исследуем погрешность аппроксимации на примере метода итераций.

Предположим, что условия теоремы о сходимости выполнены и метод итераций сходится. Оценим по модулю разность между корнем  и приближением x_n+1. Учитывая теорему Лагранжа, неравенства 0<q<1 и неравенство для модуля суммы, получим:

│ξ - x_n+1│=│(ξ) - (x_n)│=│(η)││-x_n│q│-x_n│

 q│(-x_n+1)+(x_n+1-x_n)│ q│-x_n+1│+q│x_n+1-x_n│.

Окончательно имеем │ξ - x_n+1│≤│x_n+1-x _n│.

Если ≤1 (приq0.5), то│ξ - x_n+1│≤│x_n+1-x _n│. Это означает, что если в процессе итераций выполнилось условие │x_n+1-x_n│ ε, то и│ξ - x_n+1│≤. Если же, например, q=0.9, то ==9, поэтому │ξ - x_n+1│≤9│x_n+1-x_n│, т.е. при выполнении неравенства │x_n+1-x_n│ ε близость x_n+1 к корню ξ оценивается только величиной в 9. Вообще, чем q ближе к единице, тем метод итераций сходится медленнее.

25. Метод Ньютона

Получим метод с более высокой скоростью сходимости, чем обычный метод итерации. Для этого вернемся вновь к соотношению между погрешностями на двух соседних итерациях (3):

_n+1=φ '(ξ)•ε_n+[φ ''(η)/2!]•ε²_n; η≤[a.b];

Если φ '(ξ)=0, то ε_n+1=[φ "(η)/2!]•ε²_n, что означает в силу определения 2 квадратичную сходимость итерационного процесса. Преобразуем исходное уравнение f(x)=0, умножая его на некоторую функцию -Q(x) и добавляя по x в каждую часть уравнения:

x=x-Q(x)•f(x).

Таким образом,

φ(х)=х-Q(x)•f(x); φ '(x)=1-Q'•f-Q•f '.

Подставим вместо x корень ξ:

φ '(ξ)=1-Q'(ξ)•f(ξ)-Q(ξ )•f '(ξ)=1-Q(ξ)•f '(ξ);

Для конструируемого метода надо, чтобы φ '(ξ)=0, т.е.

1-Q(ξ)•f'(ξ)=0,

следовательно Q(ξ)= ─ 1/f '(ξ).

Потребуем выполнение последнего соотношения при любом x, тогда и для конкретного значения x=ξ оно также будет выполняться, т.е.

Q(x)= ─ 1/f '(x) и φ(х)=x - ,

а итерационный метод с квадратичной сходимостью определяется формулой

x_n+1= x_n-, где n=0,1,2,… .

Этот метод называется методом Ньютона.

Теорема о сходимости метода Ньютона. Если на концах отрезка [a,b], функция f(x) принимает значения разных знаков, (то есть f(a)•f(b)<0), f '(x),f "(x) определены, непрерывны, отличны от нуля и сохраняют определенные знаки на отрезке [a,b], то исходя из начального приближения х₀[a,b], удовлетворяющего условию f(x₀)•f "(x₀)>0, то для данной функции можно методом Ньютона вычислить единственный на этом промежутке корень уравнения f(x)=0 с любой степенью точности.

Метод Ньютона имеет простую, но весьма наглядную геометрическую интерпретацию.

Запишем уравнение касательной к f(x) в точке x₀:

y(x)=f(x₀)+f '(x₀)•(x-x₀).

Найдем точку x₁―точку пересечения касательной с осью абсцисс, т.е

y(x₁)=0 или f(x₀) - f '(x₀)•(x₁-x₀)=0, откуда x₁=x₀ - .

Нетрудно заметить, что x₁ ― это первое приближение в методе Ньютона.

Аналогично получается x₂.- точка пересечения с осью абсцисс касательной, проведенной к кривой в точке x₁ – рис. 3.

Таким образом, каждая итерация в методе Ньютона геометрически интерпретируется как построение касательной, для которой находится точка пересечения ее с осью абсцисс. Поэтому метод Ньютона называют также методом касательных.

Оценка погрешности в методах Ньютона и секущих.

Квадратичный процесс в идеале, т.е. если он реализуется точно, должен давать удвоение числа верных знаков на каждой итерации, начиная с некоторой. Такой темп установления верных цифр искомого корня не только позволяет получить корень с большой точностью небольшим количеством вычислений, но и обеспечивает меньшую критичность к условию окончания процесса. Обычно, начиная уже со второй итерации, проверяют условие │x_n+1-x_n│≤ε. Этого оказывается достаточным, чтобы │ξ - x_n+1│≤. Все это справедливо и для метода секущих, только проверку начинают с третьей итерации.

26.Модификация метода Ньютона и оценки погрешности приближения.

1.Упрощенный – производная вычисляется один раз в точке x₀. x_n+1 = x_n – ;f’(x₀) = const; данный метод имеет

линейную сходимость.

Касательные параллельны

2.Метод секущих – приближенная замена производной. f’(x_n) ≈ x_n+1 = x₀ -

секущая

Для получения следующего приближения необходимо знать

предыдущие два (двухшаговый метод). x₀ и x₁ заданы изначально,

ходимость близка к квадратичной.

27.Метод хорд и оценка погрешности приближения в методе хорд.

Допустим, что на [a,b] функция f(x) меняется почти линейно. Тогда ее можно заменить стягивающей хордой y(x):

Точку пересечения хорды с осью абсцисс, где y(x₁)=0 примем за первое приближение к корню исходного уравнения

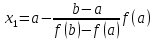аналогично

Обобщая, получим расчетную формулу x_n+1=x_n-,

где X―неподвижный конец интервала. Для сходимости метода должны быть выполнены все условия теоремы о сходимости метода Ньютона, только условие f(X)•f"(X)>0 определяет выбор неподвижного конца; противоположный конец берется за начальное приближение: f(x₀)•f "(x₀)<0.

Геометрическая интерпретация метода хорд

Оценка погрешности в методе хорд

Для метода хорд может быть получена следующая оценка:

│x_n+1-ξ│≤│x_n+1-x_n│, гдеM₁,m₁─maxиminf'(x)на отрезке [a,b].

Если M₁≤2m_1,то<1 и тогда из условия │x_n+1-x_n│ε следует выполнение условия│ξ-x_n+1│≤. Поскольку промежутки, на которых выполнены все условия теоремы сходимости, достаточно малы, то в подавляющем числе случаев условиеM₁≤2m₁ выполняется, и поэтому при реализации метода хорд ограничиваются проверкой условия │x_n+1-x_n│≤ε.

28.Понятие нормы. Нормы векторов в конечномерном пространстве.

Если x и y – элементы линейного пространства X: xX, yX, то и x+yX, и xX, где R.

Определение. Линейное пространство- нормированное, если каждому его элементу x ставится в соответствие вещественное число, называемое нормой и обозначаемое ||x||, такое, что оно удовлетворяет следующим трем аксиомам:

||x||0, причем ||x||=0 только для x=0; (аксиома неотрицательности)

||αx||=|α|·||x||, где R; (аксиома однородности)

||x+y||||x||+||y||. (аксиома треугольника)

Норма – это обобщение модуля вещественного числа на элементы линейного пространства. Нормированным пространством является множество n-мерных векторов с вещественными координатами

x= . (n - число измерений)

Это пространство обозначается Rⁿ. Для него широко используются следующие три нормы:

||x||_=max |x_i|, где 1in; (норма-максимум)

||x||₁=; (норма-сумма)

||x||₂=²; (евклидова норма)