ТУ - лекции Шмырова / Лекции по ТУ / 1

Лекция 1. Постановка задачи управления. Виды управления. Примеры.

Теория управления современная математическая наука, изучающая проблемы воздействия на динамические процессы, чаще всего описываемые обыкновенными дифференциальными уравнениями. При этом неуправляемые процессы рассматривается как частные случаи управляемых. Рассмотрим систему дифференциальных уравнений

которая описывает некоторой динамический процесс. Независимая переменная - время принадлежит отрезку [t0; T ]. x(t) - n-мерный вектор. Правая часть системы (1)

отвечает условию существования и единственности в задаче Коши. Обобщением системы (1) является система, в которой предусмотрено управление, т. е. воздействие на этот процесс, уравнения которой записываются в виде

При этом следует отметить, что в случае изучения систем типа (1) обычно решается задача нахождения функции x = x(t), удовлетворяющей некоторым краевым усло-

вием. Например, в задаче Коши ищется функция x(t), принимающая в начальный момент времени t0 заданное значение x0, ò.å.

x(t0) = x0:

По устоявшейся терминологии такого рода постановки принято называть прямыми задачами динамики. Прямая задача динамики заключается в описании движения, его свойств и выборе из семейства решений подходящей траектории. Классическим примером прямой задачи динамики является построение орбиты небесного тела по наблюдениям.

В случае, когда требуется, чтобы решение системы (2) принимало заданные зна- чения в некоторые моменты времени (или промежутки времени), решается задача нахождения такой функции

u= u(t; x);

ñкоторой решение системы (2) принимает эти заданные значения. Постановка такого рода относится к обратным задачам динамики.

Проводя классификацию задач управления можно выделить несколько основных видов:

1. Задача построения программного управления, переводящего управляемую систему из одного заданного положения в другое заданное положение. Здесь управление ищется в виде

u = u(t):

Таким образом на управлении не сказывается информация о значениях, принимаемых системой в процессе движения.

4

2. Задача построения управления в виде синтеза. Здесь требуется построить управление с учетом значений, принимаемых управляемой системой в процессе движения

u= u(t; x1; x2; : : : ; xn):

3.Задача построения оптимального управления. Здесь требуется построить такое управление, с которым некоторый специально заданный функционал

принимает минимальное (или максимальное) значение. Функционал такого рода принято называть критерием качества. Оптимальное управление может зависеть только от времени, а может быть в зависимости и от фазовых переменных. В этом случае управление называется синтезирующим. Более подробно этот вопрос будет разобран в главах, посвященных оптимальному управлению.

Приведем примеры управляемых систем и связанных с ними задач управления. Простейший пример управляемой системы может быть представлен виде

d2x = u: dt2

Если давать этому уравнению механическую интерпретацию, то роль управления здесь играет ускорение, с которым движется материальная точка с координатой x(t).

Соответственно, управляющим элементом в этой системы будет ускорение.

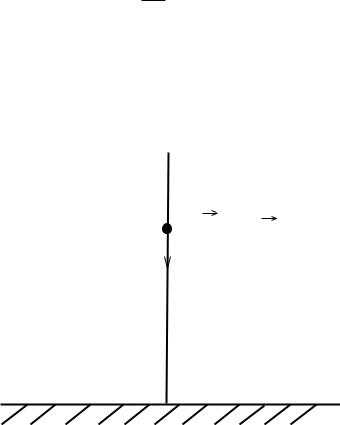
Рассмотрим движение материальной точки m по вертикальной линии под действием силы тяжести (рис. 1).

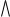
Ðèñ. 1

Пусть движение происходит по оси Ox, направленной вертикально вверх. Начало ко-

ординат поместим на земную поверхность, а положительное направление условимся отсчитывать вертикально вверх. Роль независимой переменной играет время t, à

5

искомой функцией, описывающей движение точки по действием силы тяжести является функция x = x(t). Составим уравнение для x. Механическим смыслом второй

производной в механике является ускорение (второй закон Ньюòîна). Также, принимая во внимание, что ускорение свободного падения g ¼ 9:81cm2 , с которым тело падает на землю, в нашей системе отсчета направлено со знаком минус, имеем

d2x = ¡g: dt2

Проинтегрируем это дифференциальное уравнение

dx

dt = ¡gt + C1;

gt2

x = ¡ 2 + tC1 + C2:

последнее уравнение является общим решением для x. Оно содержит две произ-

вольные константы C1 è C2. У этих констант есть конкретный физический смысл. Действительно, в начальный момент времени t = 0

¯

dx¯¯

dt ¯(t=0) = C1 = v0;

ãäå v0 начальная скорость точки. Аналогично

xjt=0 = C2 = x0;

ãäå x0 начальное положение точки. Таким образом, общее решение имеет вид

gt2

x = ¡ 2 + tv0 + x0:

Перейдем теперь к задаче управления. Если использовать управляющее ускорение, влияющее на падение точки на землю, то управляемая система будет иметь вид

d2x = ¡g + u: dt2

Решение это дифференциального уравнения при условии, что управление является постоянным (u(t) = const), имеет вид

Если теперь потребовать, чтобы в конечный момент времени t1, который заранее

неизвестнен, скорость была нулевой (мягкое приземление), то из этого условия можно определить значение управления u. Действительно

x(t) = v0 ¡ (g ¡ u)t;

и в конечный момент времени

6

x(t1) = v0 ¡ (g ¡ u)t1 = 0;

откуда

t1 = g v¡0 u:

Далее x(t1) = 0 условие приземления, откуда

u = g ¡ 2vx20 :

0

Вертикальный подъем ракеты на максимальную высоту (задача Годдарда). Ракета, имеющая в начальный момент времени начальную массу m0 верти-

кально взлетает (рис. 2).

Ðèñ. 2

В процессе сгорания топлива масса ракеты m = m(t) изменяется по формуле

m = ¡u;

ãäå u = u(t) моментальный расход топлива. Подъем ракеты заканчивается когда

масса ракеты достигнет значения m(T ) = m1, в некоторый момент времени T . На ракету действует сила тяжести

Fgr = mg

7

ãäå g ускорение свободного падения, и сила сопротивления атмосферы

Fres = av2; v = v(t) = x:

a è b предполагаются константами, связанными с техническими особенностями ра-

кеты. При включенных двигателях отрабатывается управление u = u(t) и на ракету действует сила тяги

Fact = bu:

В соответствии со вторым законом Ньютона уравнения движения ракеты имеют вид

8

< m(T ) = m1;

: v(T ) = 0;

причем конечный момент времени T не задан. Требуется найти такое управление

u = u(t), при котором максимизируется функционал, отвечающей высоте взлета ракеты

J(u) = x(T ) ! max :

Задача оптимальной остановки движения транспортного средства. Автомобиль, находящийся в начальный момент в точке x0, движется в точку x1 = 0

(ðèñ. 3).

Начальная скорость автомобиля равна v, на ускорение наложено ограничение juj · 1.

В конечный момент времени скорость автомобиля должна равняться нулю (v1 = 0). Требуется построить управление, при отработке которого автомобиль придет в

конечную точку за минимальное время. Если ввести переменные

8

Ðèñ. 3

¢

x = x1;

¢

x1 = x2;

то тогда для x1 можно дать интерпретацию переменной положения автомобиля, а x2

будет скоростью. Предполагая, что управление автомобиля реализуется с помощью ускорения, система дифференциальных уравнений, описывающих движение будет иметь вид

½x1 = x2; x2 = u;

ñграничными условиями в начальный момент времени вида

½x1(t0) = x0; :

x2(t0) = v0;

и в конечный момент времени T

½x1(T ) = 0; x2(T ) = 0:

Необходимо построить такое управление u, чтобы за наименьшее время попасть в начало координат системы (x1; x2), т. е. требуется минимизировать функционал

ZT

J[u] = dt = (T ¡ t0) ! min :

t0

9