Мат Моделирование (ЭКТ-37, Корнеев) / Capture1

3

Глава I. Постановка задачи по теплопроводности.

Имеем уравнение теплопроводности

(I.1)

Рассматриваем задачу с цилиндрической симметрией, поэтому температура зависит только от координат r, z T = T(r, z) . Коэффициент теплопроводности K дается формулой

(I.2)

где выбраны следующие значения параметров k = 2.28 mW / m , T_k = 17.5 K . Для интервала температур T = 300  2000 K коэффициент теплопроводности меняется в интервале K = 810^-3  10^-3 mW / m K . Плотность источников тепла дается формулой

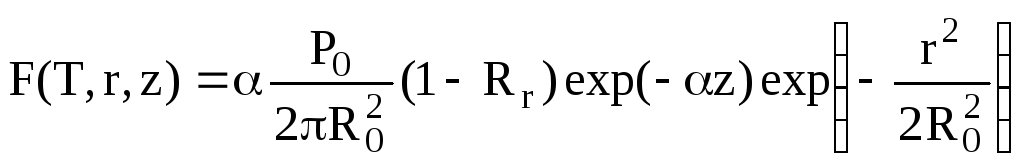(I.3)

Тепловой поток равен P₀ = 100 mW . Коэффициент отражения R_r = ((n - 1) / (n + 1))² для n = 2 равен R_r = 1/9 . Радиус источника тепла положим R₀ = 5 m . Коэффициент ослабления источника тепла вдоль оси z дается формулой

(I.4)

В указанном интервале температур, коэффициент  меняется в интервале  = 0.3  2.4 1 / m . На рис. 1 показана область действия теплового источника

Рис. 1

Уравнение (1) решаем с краевыми условиями

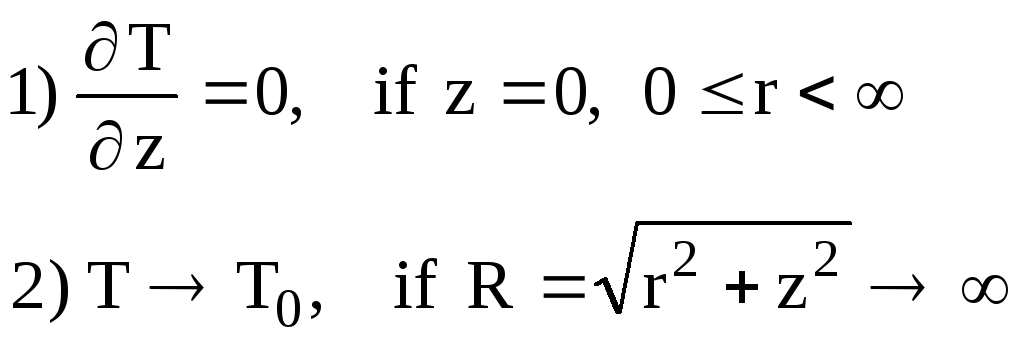(I.5)

В дальнейшем будем считать T₀ = 300 K .

Учитывая явную зависимость коэффициента теплопроводности от температуры, уравнение (1) можно упростить, введя новую функцию Y(r, z)

(I.6)

При изменении температуры в интервале T = 300  2000 K функция Y(r, z) будет меняться в интервале Y = 0  2 .

После замены (6) уравнение (1) принимает вид

(I.7)

где

(I.8)

Уравнение (7) будем решать с краевыми условиями

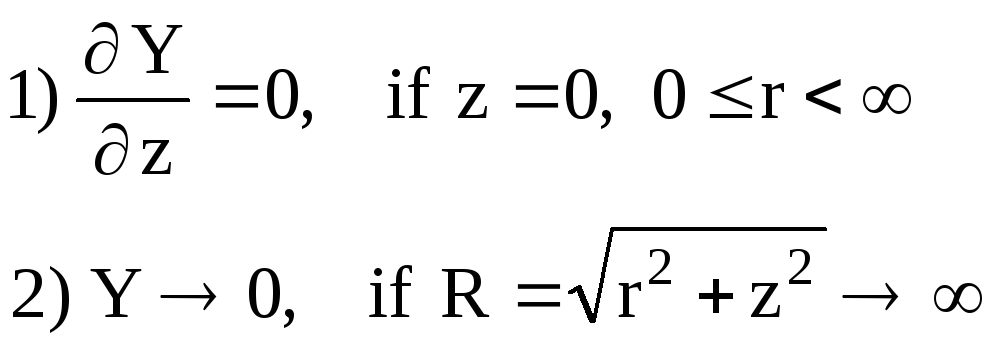(I.9)

Расширим задачу в область z < 0 для чего в правой части уравнения (7) сделаем замену . Теперь правая часть уравнения (7) будет иметь вид

(I.10)

Область действия нового теплового источника показана на рис. 2.

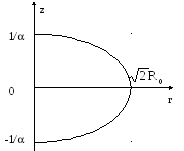
Рис. 2.

В силу симметрии задачи граничное условие

теперь выполняется автоматически. Остается граничное условие на бесконечности

(I.11)

Теперь нам надо найти решение уравнения (7) с правой частью (10) во всем трехмерном пространстве с граничным условием на бесконечности (11) . Теория потенциала позволяет свести эту задачу к решению интегрального уравнения

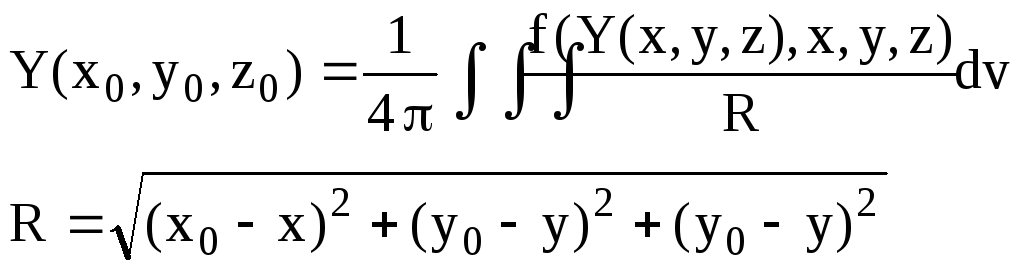(I.12)

где x₀ , y₀ , z₀ - координаты рассматриваемой точки пространства, а x , y, z - переменные интегрирования

Теперь учтем, что задача у нас цилиндрически симметричная, т.е.

Поэтому, переходя к цилиндрической системе координат, и выполняя явное интегрирование по азимутальному углу получаем интегральное уравнение в двухмерном пространстве.

(I.13)

где интегральное ядро имеет вид

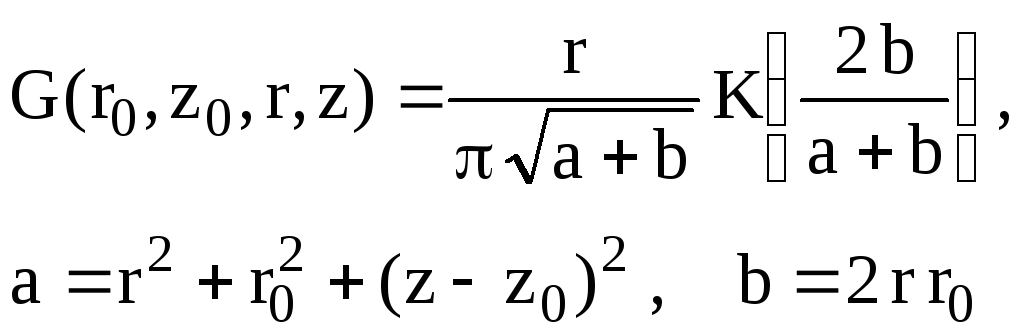(I.14)

Здесь K(m) -полный эллиптический интеграл первого рода.

И так наша задача состоит в решении нелинейного интегрального уравнения (13). Положительной стороной здесь является то, что подинтегральная функция f(Y,r,z) отлична от нуля в ограниченной области пространства. Если границы действия теплового источника выбирать там где экспоненты уменьшаются примерно в десять раз, то область интегрирования будет прямоугольником

Далее возникает проблема, как решать нелинейное интегральное уравнение (13)

На наше счастье, для наших параметров задачи, прямые итерации сходятся, примерно за десять шагов.