Мат Моделирование (ЭКТ-37, Корнеев) / Capture3

17

Глава III. Алгоритм численного взятия интеграла

Нас интересует алгоритм вычисления двукратного интеграла с сингулярным ядром в виде эллиптического интеграла первого рода.

(III.1)

где

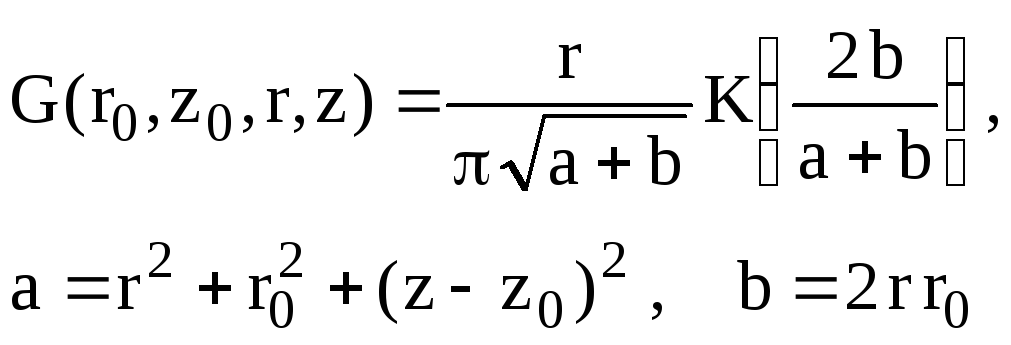(III.2)

Здесь K(m) -полный эллиптический интеграл первого рода.

(III.3)

Выбираем прямоугольную сетку в окне интегрирования 0  r  L_r , -L_z  z  L_z

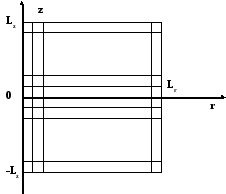
Интеграл (1) равен сумме интегралов по элементарным прямоугольникам rz выбранной сетки. Центры прямоугольников имеют координаты (r_n , z_k) где

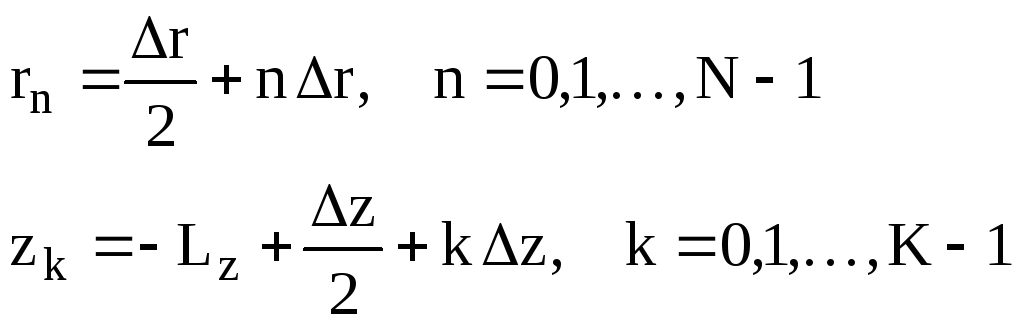(III.4)

Стороны прямоугольников равны

(III.5)

Число отрезков K по оси 0z должно быть четным.

Значения интеграла (1) будем находить в центрах элементарных прямоугольников, т.е.

(III.6)

Таким образом, интеграл (1) заменяем суммой интегралов

(III.7)

где

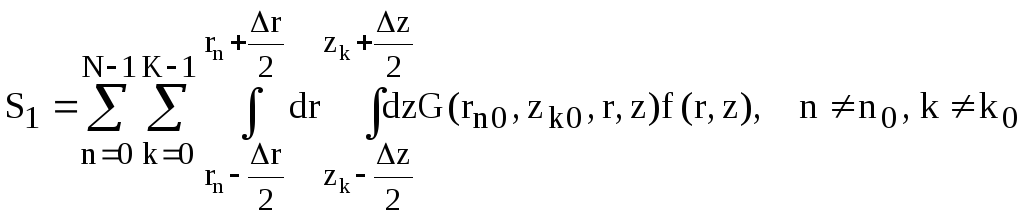(III.8)

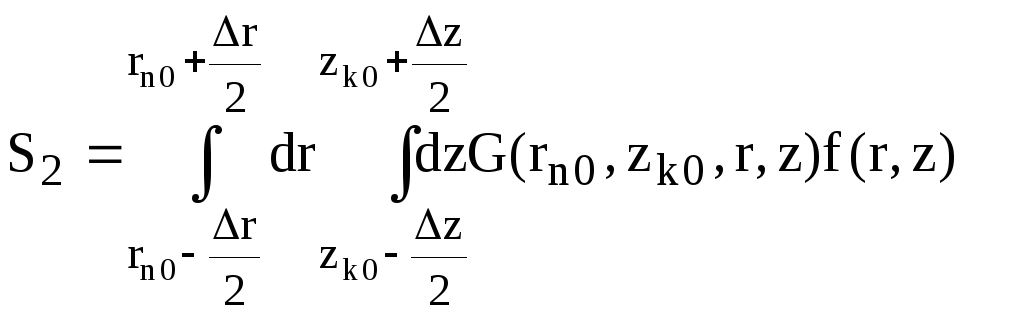(III.9)

Интегралы в сумме (8) вычисляем по формуле

(III.10)

где остаточный член равен

и где лежат в прямоугольнике rz . Если положить r = z = h и считать, что подынтегральная функция достаточно медленно меняется в прямоугольник rz , то ошибка интегрирования будет иметь порядок

Таким образом, ошибка вычисления одного интеграла I_nk в сумме S₁ имеет порядок h⁴ . Поэтому ошибка вычисления всей суммы S₁ имеет порядок NKh⁴ = 2L_zL_rh² .

Ядро интеграла G(r₀ , z₀ , r, z) имеет сингулярность при r₀ = r, z₀ = z . Поэтому интеграл S₂ надо вычислять с учетом сингулярности. Воспользуемся тем, что f(r, z) в прямоугольнике rz меняется медленно. Поэтому получаем

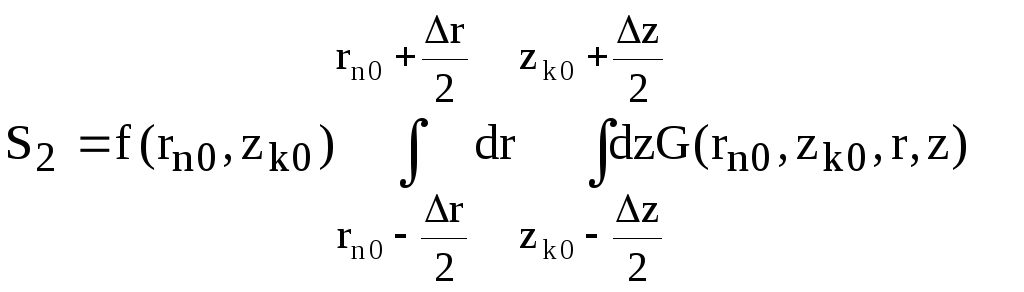(III.11)

Учтем что

Делаем замену переменных в интеграле (11)

Интеграл (11) принимает вид

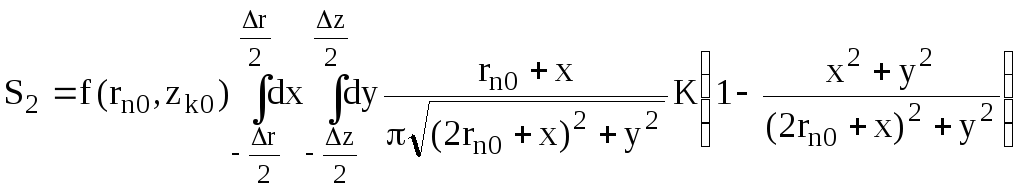(III.12)

Подынтегральная функция имеет сингулярность в точке x = 0 , y = 0 . Вблизи этой точки будем использовать асимптотическое разложение полного эллиптического интеграла K(m) . Чтобы исследовать точность вычисления интеграла при такой замене, применим этот метод к интегралу, который вычисляется точно. Возьмем для примера следующий двукратный интеграл

(III.13)

Сначала вычислим этот интеграл, перейдя к одномерному интегралу.

(III.14)

Разбиваем интервал [0…1] на N отрезков длиной  = 1/N . Интеграл (14) разбиваем на N интегралов

(III.15)

В интеграле, в последнем члене суммы (15), для переменной интегрирования имеем оценку    << 1 . Поэтому используем асимптотическое выражение для эллиптического интеграла

(III.16)

Поэтому интеграл в (15) вычисляем с учетом (16)

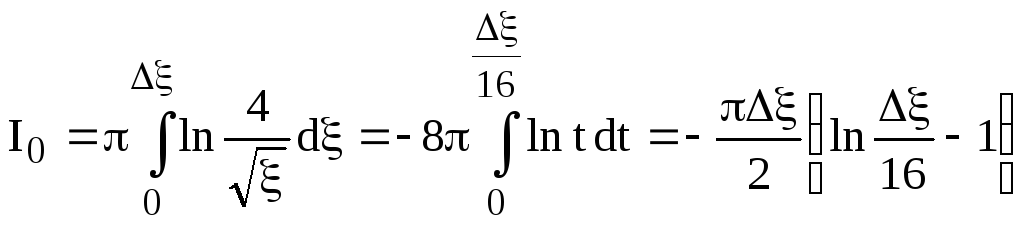(III.17)

Интеграл (14) вычисляем по формуле

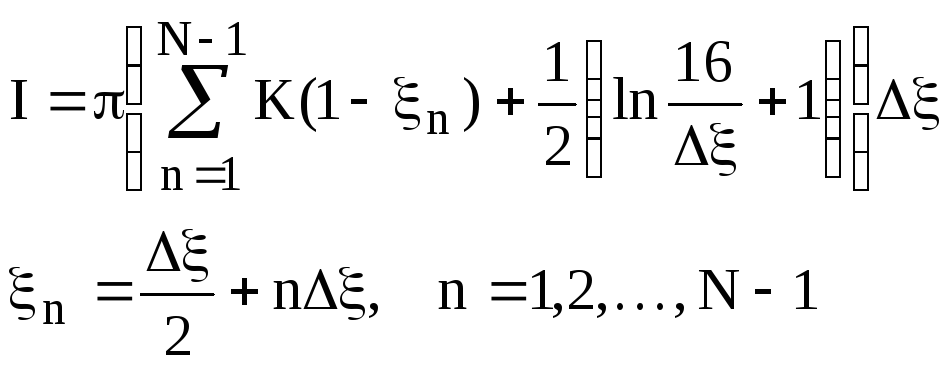(III.18)

Формула (18) проверяется в программе test2.cpp . Результаты работы программы представлены в таблице 1. Здесь представлена зависимость относительной ошибки вычисления интеграла I = (I - 2) / 2 от размеров интервала 

Таблица 1

	0.5	0.25	0.2	0.1
	0.02	0.0074	0.005	0.002

Из таблицы видно, что асимптотика (16) достаточна для точного вычисления интеграла. Дело в том, что первые N-1 членов в сумме (15) вычисляются по формуле прямоугольников и имеют точность порядка ² . Последний интеграл в (15), вычисленный по формуле (16) имеет не меньшую точность.

Теперь интеграл (13) будем вычислять как двумерный интеграл. Выберем сетку для интегрирования, следующего вида

Введем координаты центров прямоугольников

Числа N, M должны быть нечетными. В незашрихованных прямоугольниках интеграл вычисляется по обычным формулам (формула прямоугольников, двумерная), аналогично тому, как это делалось в (10).

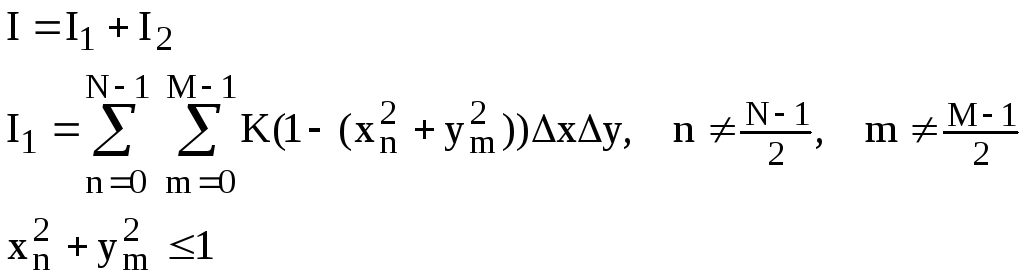(III.19)

В зашрихованном прямоугольнике интеграл будем вычислять с учетом асимптотики (16)

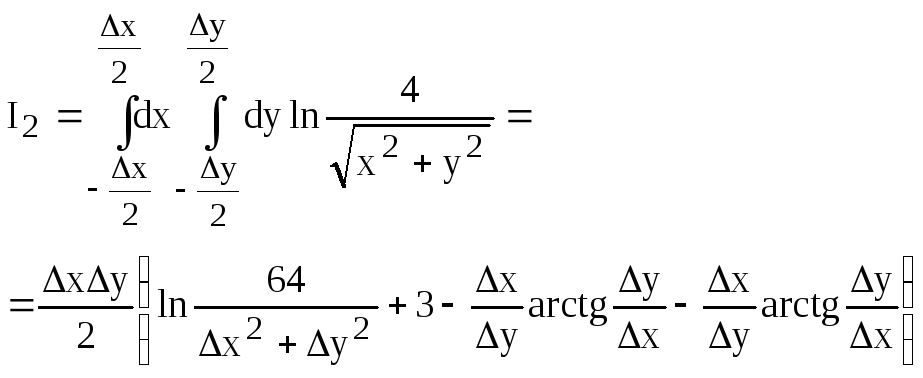(III.20)

Формулы (19), (20) проверяется в программе test3.cpp . Отметим, что здесь имеется еще одна проблема, не относящаяся к вопросу выбора асимптотики. Из рисунка видно, что граница интегрирования это окружность, а прямоугольная сетка лишь приближенно описывает круг. Идея состоит в дополнительном разбиении прямоугольников, содержащих элементы границы (окружности), на более мелкие части, пока изрезанность границы перестанет влиять на конечный результат. Эта идея была реализована с помощью рекурсивной функции Ordinary . Приведем основные функции необходимые для вычисления интеграла (13).

Здесь Kellip1 функция для вычисления полного эллиптического интеграла K(m) .

double Kellip1(double m)

{

double a0 = 1.38629, b0 = 0.5;

double a1 = 0.1119723, b1 = 0.1213478;

double a2 = 0.0725296, b2 = 0.0288729;

double m1 = 1 - m;

return (a0 + a1*m1 + a2*m1*m1) + (b0 + b1*m1 + b2*m1*m1)*log(1/m1);

}

Функция Singular вычисляет сингулярный интеграл I₂ в формуле (20)

double Singular(double x, double y)

{

double f;

f = log(64./(x*x + y*y)) + 3;

f = f - (x/y)*atan(y/x) - (y/x)*atan(x/y);

return f*x*y/2.;

}

Функция Conclude определяет, содержит ли заданный прямоугольник сетки интегрирования границу круга x² + y² <=1 . Здесь x, y -координаты центра прямоугольник, а dx, dy -стороны этого прямоугольника.

double Conclude(double x, double y, double dx, double dy)

{

double R1, R2, R3, R4;

R1 = (x-0.5*dx)*(x-0.5*dx) + (y-0.5*dy)*(y-0.5*dy);

R2 = (x+0.5*dx)*(x+0.5*dx) + (y-0.5*dy)*(y-0.5*dy);

R3 = (x+0.5*dx)*(x+0.5*dx) + (y+0.5*dy)*(y+0.5*dy);

R4 = (x-0.5*dx)*(x-0.5*dx) + (y+0.5*dy)*(y+0.5*dy);

if(R1<1 && R2<1 && R3<1 && R4<1)

return 1;

else

if(R1>1 && R2>1 && R3>1 && R4>1)

return 0;

else

return 2;

}

double Ordinary(double x, double y, double dx, double dy)

{

double dx0, dy0, x0, y0;

double S = 0;

int kluch = Conclude(x,y,dx,dy);

if(kluch == 0) return 0;

if(kluch == 1 || (dx<=0.0001 && dy<=0.0001))

return Kellip1(1-x*x-y*y)*dx*dy;

if(kluch == 2)

{

dx0 = dx/2., dy0 = dy/2.;

for(int n=0; n<2; n++)

for(int m=0; m<2; m++)

{

x0 = x - dx0/2. + n*dx0;

y0 = y - dy0/2. + m*dy0;

S += Ordinary(x0,y0,dx0,dy0);

}

}

return S;

}

Результаты работы test3.cpp приведены в таблице 2 . Здесь представлена зависимость относительной ошибки вычисления интеграла I = (I - 2) / 2 от размеров интервала h = x = y

Таблица 2

H	0.66	0.40	0.22	0.1
	0.0025	0.00074	0.00024	0.00002

Из таблиц 1 и 2 можно определить при каких значениях аргумента  эллиптического интеграла K(1 - ) можно использовать асимптотику (16) . Мы видим, что относительная ошибка вычисления одномерного интеграла порядка 0.001 достигается при =0.1 . Для двукратного интеграла такая же точность достигается, если  = x² + y² = (x/2)² +(y/2)²  0.1 . Сделаем теперь вывод , чтобы точность вычисления интеграла с сингулярностью была не менее 0.001, надо асимптотику применять для аргумента <=0.1

Вычисление интеграла (12)

Теперь можно вычислить интеграл (12) с заданной точностью. Для этого разобьем прямоугольник rz интегрирования следующей сеткой.

Интеграл (12) разобьем на сумму интегралов по каждому прямоугольнику сетки интегрирования. Интегралы по не заштрихованным прямоугольникам вычисляются обычным способом. Берется подинтегральная функция в центре прямоугольника и умножается на площадь этого прямоугольника.

(III.21)

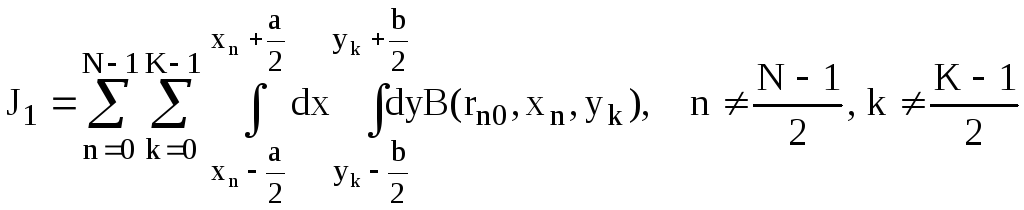
где

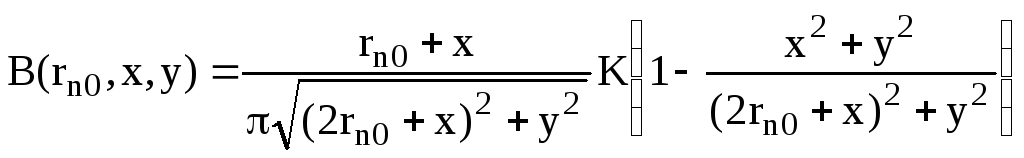
Здесь N, K – нечетные числа и выбираются из условия выполнения асимптотики (16)

В зашрихованном прямоугольнике интеграл будем вычислять с учетом асимптотики (16) аналогично формуле (20)

(III.22)

Используя формулы (21) , (22) вычисляем интеграл S₂ с относительной ошибкой не более 0.001 .

Итог. Описание алгоритма вычисления интеграла

Итак, мы должны вычислить интеграл (1)

(III.23)

где функция f(r,z) локализована в некоторой области D , и достаточно быстро спадает до нуля вне этой области. D.

1. Выбираем окно интегрирования 0  r  L_r , -L_z  z  L_z включающее область D . Размеры окна интегрирования выбираем, используя рекомендации главы «Решение нелинейного уравнения Пуассона, Оценка ошибки при выборе окна интегрирования» .

2. Выбираем сетку интегрирования. Определяем координаты центров элементарных прямоугольников сетки

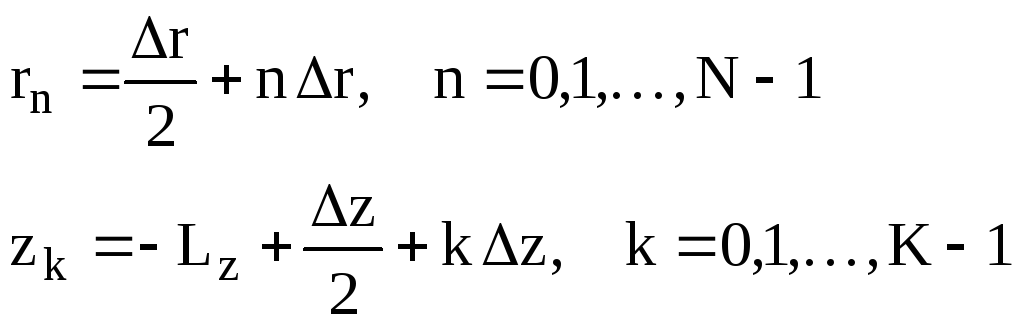
Число K должно быть четным.

3. Интеграл (23) разбивается на сумму интегралов по элементарным прямоугольникам сетки D_nk

(III.24)

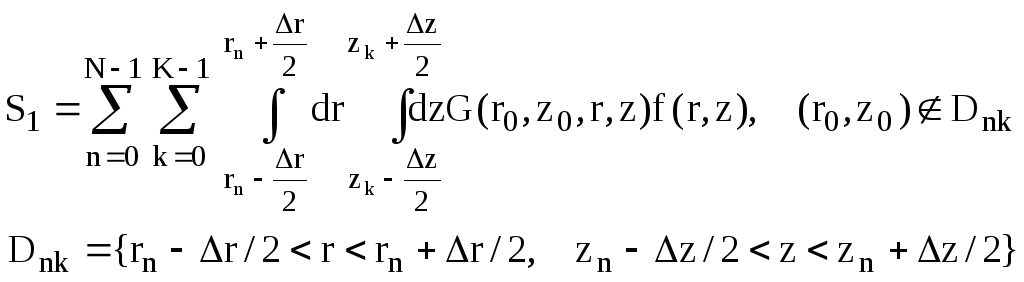(III.25)

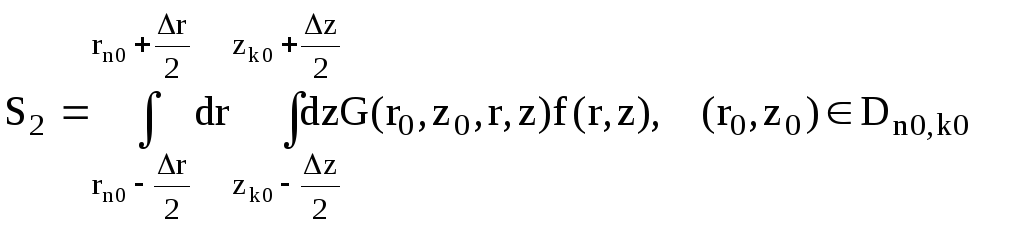(III.26)

Из суммы (24) выделен член S₂ , который равен интегралу по прямоугольнику D_n0,k0 , содержащему точку (r₀, z₀) . Этот интеграл надо вычислять с учетом асимптотики (16).

4. Интеграл (23) будем вычислять в центрах элементарных прямоугольников

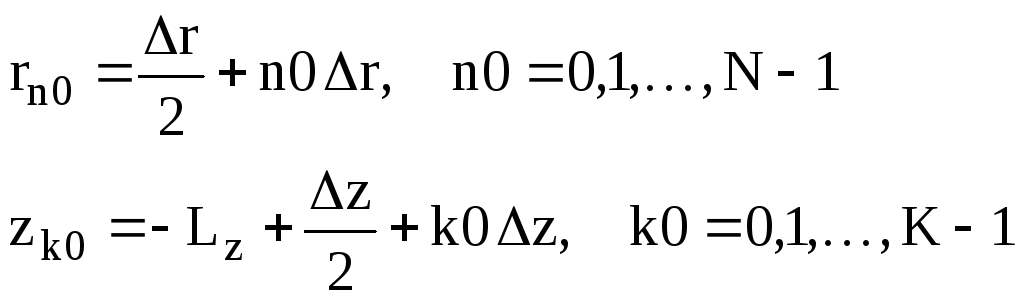
4. Интегралы в сумме (25) вычисляем по формуле

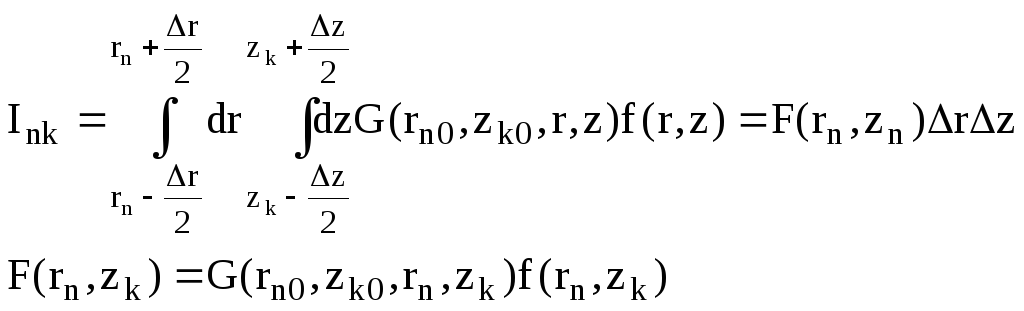(III.10)

4. Интеграл S₂ в (26) вычисляем по формулам (21), (22)

5. Выбираем функцию f(r, z) из тестовых задач (Пример 2 и Пример 3 из главы Решение нелинейного уравнения Пуассона) и сравниваем известные результаты с вычисленным интегралом (23). Меняя размеры r, z элементарных прямоугольников интегрирования D_nk , находим условия, при которых можно достигнуть заданной точности вычисления интеграла (23) .