
u_practice
.pdf
а) kfk ≥ 0, причем kfk = 0 только для f = o,
б) kcfk = |c| kfk при произвольном вещественном c и f F ,
в) kf1 + f2k ≤ kf1k + kf2k для любых f1, f2 F (неравенство треугольника).
Определение 9.3. Последовательность fm, m = 1, 2, ... элементов из F называется фундаментальной, если > 0 N = N( ) такое, что k, m >
Nkfk − fmk < .
Определение 9.4. Линейное нормированное пространство называется
полным, если для любой фундаментальной последовательности его элементов найдется элемент этого пространства, к которому она сходится.
Полное линейное нормированное пространство B называется банаховым пространством.
Определение 9.5. Будем говорить, что в линейном пространстве H введено скалярное произведение, если любой паре элементов h1, h2 H поставлено в соответствие вещественное число (h1, h2) (скалярное произведение этих элементов), и это соответствие обладает следующими свойствами:
а) (h1, h2) = (h2, h1),
б) (h1 + h2, h) = (h1, h) + (h2, h),
в) для любого вещественного c верно (ch1, h2) = c(h1, h2), г) (h, h) ≥ 0, причем (h, h) = 0 только при h = o.
Определение 9.6. Линейное пространство H со скалярным произведе-
p
нием, полное в норме khk = (h, h), порождаемой этим скалярным произведением, называется гильбертовым пространством.
Определение 9.7. Множество R B называется плотным в нормированном пространстве B, если для любого элемента f B существует последовательность fk, fk R, k = 1, 2, ..., сходящаяся к f (fk → f при k → ∞).
Определение 9.8. Множество Ω Em называется множеством (лебеговой) меры нуль, если для любого ε > 0 можно найти покрывающее его счетное множество открытых (m – мерных) кубов, сумма объемов которых меньше ε.
Определение 9.9. Если некоторое свойство выполнено всюду в Ω Em за исключением, может быть, множества меры нуль, то говорят, что это свойство выполнено почти всюду в Ω (записывают п.в. в Ω).
Определение 9.10. Функция, определенная в области Ω, называется измеримой в Ω, если она является пределом п.в. в Ω сходящейся последовательности функций, непрерывных на Ω.
Определение 9.11. Неотрицательная п.в. в Ω функция f(x) называется интегрируемой по Лебегу в Ω, если существует п.в. в Ω сходящаяся к ней
51
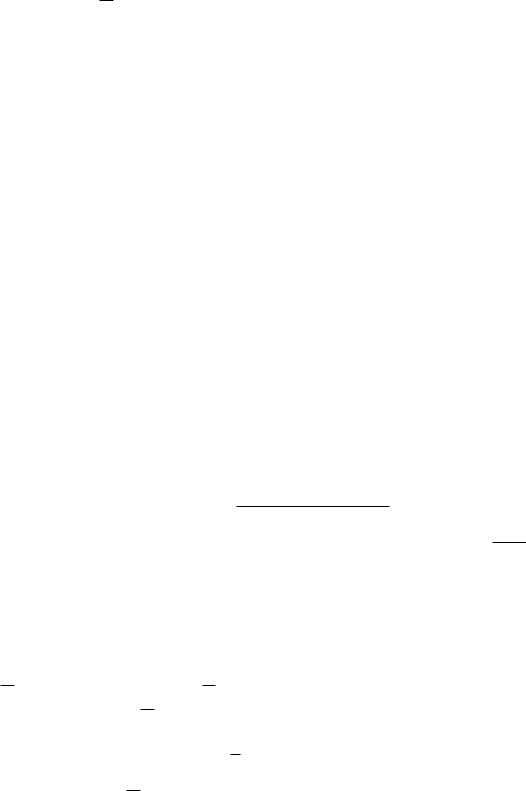
монотонно неубывающая последовательность fk(x), k = 1, 2, ..., функций,
непрерывных на Ω с ограниченной сверху последовательностью интегралов
R
(Римана): fk(x) dx ≤ C, k = 1, 2, .... При этом точная верхняя грань мно-
f(x): |
Ω |
|
|
|
|
|
|
|
|
|
R |
|
k = 1, 2, ...} называется интегралом Лебега функции |
||||||||
жества { |
fk(x) dx, |
|||||||||
Ω |
Z |
|
Z |
|
|
= k→∞ Z |
|
|
|
|
|
L |
k |
k( ) |
dx |
f |
k |
(x) dx. |
|||
|
( ) |
f(x) dx = sup |
|
f x |
lim |
|
||||
|
|
Ω |
|
Ω |
|
|
Ω |
|
|
|
Определение 9.12. Функция f(x) называется интегрируемой по Лебегу по области Ω, если ее можно представить в виде разности f(x) = f1(x) − f2(x) двух неотрицательных функций, интегрируемых по Лебегу. При этом интеграл Лебега от функции f(x) определяется равенством
(L) Z |
f(x) dx = (L) Z |
f1(x) dx − (L) Z |
f2(x) dx. |
Ω |
Ω |
Ω |
|
Определение 9.13. Множество измеримых по Лебегу на Ω и интегрируемых по Лебегу по области Ω функций обозначается L1(Ω).
Определение 9.14. Множество измеримых и интегрируемых с квадратом по Лебегу по области Ω функций обозначается L2(Ω).
Введем обозначения
Dαf(x) = ∂|α|f(x1, x2, ..., xm).
Здесь α = (α1, α2, ..., αm) – мультииндекс, αi ≥ 0 -целые, i = 1, m, |α| =
α1 + α2 + ... + αm.
Определение 9.15. Пространство функций, непрерывных на множестве Ω Em, обозначают C(Ω).
Пространство C(Ω) является линейным пространством. Определение 9.16. Пространство функций, непрерывных на множе-
стве Ω Em, обозначают C(Ω).
В пространстве C(Ω) вводится норма
||u||C(Ω) = max |u(x)|.
Ω
Пространство C(Ω) является банаховым пространством. Определение 9.17. Пространство функций, непрерывно дифференци-
руемых до порядка k включительно на множестве Ω Em, обозначают
Ck(Ω):
Ck(Ω) = {f(x)| Dαf(x) C(Ω) α, |α| ≤ k} .
52

Пространство Ck(Ω) является линейным пространством. Определение 9.18. Пространство функций, непрерывно дифференци-
руемых до порядка k включительно на множестве Ω Em, обозначают
Ck(Ω):
Ck(Ω) = f(x)| Dαf(x) C(Ω) α, |α| ≤ k .
В пространстве Ck(Ω) вводится норма
|
|X |
||u||Ck(Ω) = |
||Dαf(x)||C(Ω). |
|
α|≤k |
Пространство Ck(Ω) является банаховым пространством. Определение 9.19. Пространство функций, измеримых по Лебегу на
множестве Ω Em и интегрируемых по Лебегу со степенью p, обозначают
Lp(Ω):
Lp(Ω) = {f(x)| f(x)измеримы по Лебегу и Z |
|f|p(x) dx < ∞}. |
Ω |
|
Впространстве Lp(Ω) вводится норма
1/p
||u||Lp(Ω) = |
Z |
|f(x)|p dx |
|
. |
|
Ω |
|
|
Пространство Lp(Ω) является банаховым пространством. Определение 9.20. Пространство функций, измеримых по Лебегу на
множестве Ω Em и интегрируемых по Лебегу со степенью p на любом Ω0, строго вложенном в Ω, обозначают Lp,loc(Ω).
Заметим, что Lp(Ω) Lp,loc(Ω).
Определение 9.21. Последовательность fm, m = 1, 2, ..., элементов из H называется сходящейся сильно к элементу f из H (fm → f при m → ∞), если kf − fmkH → 0 при m → ∞.
Определение 9.22. Последовательность fm, m = 1, 2, ..., элементов из H называется сходящейся слабо к элементу f из H (fm → f при m → ∞), если для любого h H (fm, h) → (f, h) при m → ∞.
Задачи и упражнения
9.1. Установить, что следующие множества являются множествами меры нуль в m-мерном пространстве:
53

1)конечное множество точек,
2)счетное множество точек,
3)пересечение счетного множества множеств меры нуль,
4)объединение счетного множества множеств меры нуль,
5)гладкая (m − 1) – мерная поверхность,
6)гладкая (k) – мерная поверхность (k ≤ m − 1).
9.2.При каких значениях α интегрируемы по шару |x| < 1 следующие
функции:
а) f(x) = |x1|α ; б) f(x) = (1−1|x|)α .
Доказать следующие утверждения:
9.3.Если f, g L1(Ω), то αf + βg L1(Ω) при любых постоянных α и β.
9.4.Если f1, f2 L2(Ω), то αf1 + βf2 L2(Ω) при любых постоянных α и
β.
9.5.Ни одно из включений: L1(Em) L2(Em), L2(Em) L1(Em) места не имеют.
9.6.Если f, g L2(Ω), то f · g L1(Ω).
9.7. Если f, g L2(Ω), то имеет место неравенство Буняковского
|
|
1/2 |
1/2 |
Z |
f · g dx |
≤ |
Z |
|f|2 dx |
Z |
|g|2 dx |
|
. |
|
|
|
|
|
|
|
|
|
|
Ω |
Ω |
Ω |
9.8. Если f, g L2(Ω), то имеет место неравенство Минковского
Z |f + g|2 dx 1/2 |
≤ |
Z |f|2 dx 1/2 |
+ |
Z |g|2 dx 1/2 . |
|||
Ω |
|
|
Ω |
|
|
Ω |
|
9.9. Найти интегралы по отрезку [0, 1] от следующих функций (предвари-
тельно доказав их интегрируемость): |
|
|||||||
|
|
0, |
x − |
рационально; |
|
|||
а) f(x) = |
|
x2, |
x − |
иррационально, |
|
|||
|
|
x2, |
|
|
x |
|
иррационально и больше |
1/3, |
б) f(x) = |
x3, |
|
еслиx |
иррационально и меньше 1/3, |
||||
|
|
0, |
|
если x |
|
рационально; |
|
|
|
sin πx, |
|
если |
x |
иррационально и меньше |
1/2, |
||
в) f(x) = |
|
x2, |
|
если |
x |
иррационально и больше |
1/2, |
|
|
|
0, |
|
если |
x рационально; |
|
||
|
|
|
|
|
|
|
|
|
54

г) f(x) = |
1/n, |
|
|
|
|
|
если |
x = m/n, где m, n взаимно просты, |
|||||||||||||||
0, |
|
|
|
|
|
если |
x иррационально; |
||||||||||||||||
д) f(x) = |
x−1/3, |
|
|
|
|
если |
|
x |
иррационально, |
||||||||||||||
x3, |
|
|
|
|
|
|
если |
|
x |
рационально; |
|||||||||||||
е) f(x) = sign sin |
π . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
можно ввести норму следующим образом: |
||||||||||
9.10. Убедиться, что в Em |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
x2 |
1/2 |
|
||
а |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
||
) |
| |
x |
|∞ |
= max |
| |
x |
i| |
; |
) |
| |
x |
|2 |
= |
|
|
|
. |
||||||
|
|
1≤i≤m |
|
|
|
|
|
i=1 |
i |
|
|
|
|||||||||||
Здесь x = (x1, . . . , xm). |
|
|
|
|
|
P |
|
|
|
|
|||||||||||||
9.11. Показать, что в пространствах L1(Ω) и L2(Ω) можно ввести нормы |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||f||L1(Ω) = Z |
|f| dx; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||f||L2 |
(Ω) = |
Z |
|f|2 dx |
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
Доказать следующие утверждения:
9.12.Если последовательность fk(x), k = 1, 2, ..., функций из L2(Ω) сходится к f(x) по норме L2(Ω), то она сходится и слабо к f(x) в L2(Ω).
9.13.Если последовательность fk(x), k = 1, 2, ..., функций из L2(Ω) сходит-
RR
ся к f(x) по норме L2(Ω), то fk dx → f dx, k → ∞ (Ω - ограниченная
ΩΩ
область).
∞
P
9.14. Если uk L2(Ω), k = 1, 2, ..., и ряд uk(x) сходится к u(x) по норме
k=1
∞
kP |
R |
R |
Ω |
Ω |
|
L2(Ω), то |
|
uk dx = u dx (Ω - ограниченная область). |
=1 |
|
|
9.15.Если последовательность fk(x), k = 1, 2, ..., функций из C(Ω) сходится к f(x) равномерно в Ω, то она сходится и по норме L2(Ω) (Ω - ограниченная область).
9.16.Если последовательность fk(x), k = 1, 2, ..., функций из L2(Ω) схо-
дится слабо к f(x) L2(Ω), то последовательность норм ||fk(x)||L2(Ω), k = 1, 2, ..., ограничена.
9.17. Если последовательность fk(x), k = 1, 2, ..., функций из L2(Ω) сходится слабо к f(x) L2(Ω) и ||fk(x)|| → ||f(x)|| при k → ∞, то эта последовательность сходится к f(x) и по норме L2(Ω).
55

10. Обобщенные производные. Пространства Соболева
Пусть Ω Em некоторая ограниченная область с гладкой границей
∂Ω.
Пограничной полосой области Ω называется совокупность точек этой области, обладающих тем свойством, что их расстояние до ∂Ω не превосходит заданной постоянной δ > 0, называемой шириной полосы.
Определение 10.1. Функция g(x) называется финитной в области Ω,
если она обращается в ноль в некоторой пограничной полосе области Ω.
◦
Пространство непрерывных финитных в Ω функций обозначается C (Ω).
Пространство k раз непрерывно дифференцируемых финитных в Ω функ-
◦
ций обозначается Ck (Ω).
Определение 10.2. Функция fα(x) L2,loc(Ω) называется обобщенной производной по Соболеву порядка α функции f(x) L2,loc(Ω), если для
◦
любой функции g(x) C|α| (Ω) имеет место равенство
Z |
fDαg dx = (−1)|α| |
Z |
fαg dx. |
Ω |
|
Ω |
|
Определение 10.3. Множество функций, имеющих все обобщенные производные до порядка k включительно, принадлежащие пространству
L2(Ω), обозначим Hk(Ω): |
|
|
|
|
Hk(Ω) = {f(x)| Dαf(x) L2(Ω) |
α, |α| ≤ k}. |
|||
В пространстве Hk(Ω) вводится норма |
|
|
||
||u||Hk(Ω) = |
Z |
α k(Dαu)2 dx |
1 |
|
2 . |
||||
|
|
|X |
|
|
|
Ω |
|≤ |
|
|
Пространства Hk(Ω) называют пространствами Соболева.
Определение 10.4. Следом f|S функции f C(Ω) на (m−1) – мерной поверхности S называется значение на этой поверхности функции, которая определена в каждой точке, непрерывна в Ω и почти всюду совпадает с f на S.
Верна
лемма о следе. Пусть S – некоторая (m − 1) – мерная поверхность, лежащая в Ω. Тогда для любой функции f H1(Ω) имеет место неравенство
kf|SkL2(S) ≤ CkfkH1(Ω), C > 0.
56

Здесь константа C не зависит от функции f.
Из леммы о следе следует, что если fk(x), k = 1, 2, ... - последовательность функций из C1(Ω), сходящаяся в норме H1(Ω) к f(x), S - гладкая (m − 1)-мерная поверхность, лежащая в Ω, то последовательность следов функций fk(x) на S сходится в норме L2(S) к некоторой функции g(x) L2(S), которую называют следом f|S функции f(x) на поверхности S Ω. Доказывается, что f|S не зависит от выбора последовательности fk(x).
Пример 10.1. Определить след функции
f = |
2, |
||x|| = 1 |
|
|
1, |
x |
< 1, |
на границе области Ω = {x | |
|x| |
< 1}, x Em (∂Ω = {x| |
|
|x| = 1}). |
|
|
|
Решение. Рассмотрим последовательность заданных на Ω функций fk(x) ≡ 1, k = 1, 2, . . . . Так как fk = f при x Ω и обобщенные производные (здесь обобщенные производные в области Ω совпадают с классиче-
скими) ∂fk = ∂f , i = 1, m, при x Ω, то для функций fk и f имеет место
∂xi ∂xi
тождество kf(x) − fk(x)kH1(Ω) = 0, k = 1, 2, . . . . То есть fk(x) → f(x) при k → ∞ по норме пространства H1(Ω). След fk|∂Ω непрерывной в Ω функции fk, k = 1, 2, . . . , на границе ∂Ω равен 1. Предел последовательности
fk|∂Ω в норме пространства L2(∂Ω) равен 1. Значит, f|∂Ω = 1.
◦
Определение 10.5. Замыкание пространства Ck (Ω) в норме простран-
◦
ства H1(Ω) обозначается Hk (Ω).
◦
Замечание. Если функция f H1 (Ω), то ее след f|∂Ω на границе
области Ω равен нулю.
◦
Действительно, из определения пространства H1 (Ω) следует, что для
◦
любой функции f H1 (Ω) существует последовательность {fk(x)}k∞=1 |
||||||||||||
◦ |
(Ω) такая, что |
k |
|
− |
|
kH1 |
→ |
0 при k |
→ ∞ |
| |
|
= 0. |
C∞ |
|
fk(x) |
|
f(x) |
◦ |
|
|
. След fk |
∂Ω |
|||
Согласно лемме о следе имеет место неравенство |
|
|
|
|
||||||||
|
kfk|∂Ω − f|∂ΩkL2(∂Ω) = kf|∂ΩkL2(∂Ω) ≤ ckfk − fkH1(Ω). |
|
|
|||||||||
Из последнего неравенства получаем, что kf|∂ΩkL2(∂Ω) = 0. Отсюда f|∂Ω = 0.
Определение 10.6. Два скалярных произведения (u, v)I и (u, v)II и соответсвующие им нормы ||u||I и ||u||II называются эквивалентными в
57
гильбертовом пространстве H, если существуют постоянные c1 > 0 и c2 > 0 такие, что для любого u H справедливы неравенства c1||u||I ≤ ||u||II ≤ c2||u||I .
Верно
неравенство Стеклова (Пуанкаре-Фридрихса)
ZZ
f2 dx ≤ c |
|rf|2 dx, |
Ω |
Ω |
◦
которое справедливо для функций из пространства H1 (Ω), здесь c > 0 – постоянная, зависящая только от свойств области Ω.
◦
Пример 10.2. Доказать, что скалярные произведения в H1 (Ω)
Z
(f, g) = [fg + rf · rg] dx,
Ω
Z
(f, g)I = [| sin |x||fg + 2rf · rg] dx
Ω
эквивалентны.
Решение. Скалярные произведения эквивалентны, если эквивалентны порождаемые ими нормы
kfk2 = |
Z [f2 + |rf|2] dx , |
|
|
Ω |
|
Z
kfk2I = [| sin x|f2 + 2|rf|2] dx ,
Ω
то есть если существуют костанты c1 > 0 и c2 > 0 такие, что для любой
◦
функции f H1 (Ω)
c1kfk ≤ kfkI ≤ c2kfk.
Рассмотрим первое неравенство, учитывая, что | sin |x|| ≥ 0,
kfkI2 = Z |
[| sin x|f2 + 2|rf|2] dx ≥ Z |
2|rf|2 dx = Z (|rf|2 + |rf|2) dx, |
Ω |
Ω |
Ω |
используя неравенство Стеклова (Пуанкаре-Фридрихса)
ZZ
f2 dx ≤ c |
|rf|2 dx, |
Ω |
Ω |
58
◦
которое справедливо в пространстве H1 (Ω), получим |
|
||||||||
kfkI2 ≥ (|rf|2 + |rf|2) dx ≥ (1c f2 |
+ |rf|2) dx ≥ |
|
|||||||
|
R |
|
2 |
2 |
R |
2 |
|
||
|
Ω |
R |
|
|
Ω |
|
|
||
min{1/c, 1} |
(f |
|
+ |rf| ) dx = min{1/c, 1}kfk , |
|
|||||
|
|
|
|
Ω |
|
|
|
|
|
таким образом, c1 = (min{1/c, 1})1/2. |
|
|
|
||||||
Рассмотрим |
второе |
|
неравенство, |
учитывая, |
что |
||||
| sin |x|| ≤ 1, |
|
|
|
|
|
|
|
|
|
kfkI2 = Z [| sin x|f2 + 2|rf|2] dx ≤ 2 Z [f2 + |rf|2] dx = 2kfk2, |
|
||||||||
Ω |
|
|
|
|
|
|
Ω |
|
|
таким образом, c2 = √ |
|
. |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
Задачи и упражнения
10.1.Установить, что смешанная о.п. не зависит от порядка дифференцирования.
10.2.Показать, что из существования о.п. Dαf не следует, вообще говоря, существования о.п. Dα0 f при αi0 ≤ αi, i = 1, ..., m, |α0| < |α|.
Указание. Рассмотреть функцию f(x1, x2) = f1(x1) + f2(x2), где fi не имеют обобщенной производной первого порядка по xi.
10.3. Показать, что если в области Ω функция f(x) имеет о.п. Dαf, то и
в любой подобласти Ω0 Ω функция f(x) имеет на Ω0 о.п. fα и fα = Dαf на Ω0.
10.4. Пусть в области Ω1 задана функция f1(x), имеющая о.п. Dαf1, а в области Ω2 функция f2(x), имеющая о.п. Dαf2. Доказать, что если Ω1 Ω2область, и для x Ω1 ∩ Ω2, f1(x) = f2(x), то функция
|
f2(x), |
x Ω2 |
, |
f(x) = |
f1(x), |
x Ω1 |
, |
имеет о.п. Dαf в Ω1 Ω2, равную Dαf1 в Ω1 и Dαf2 в Ω2. 10.5. Пусть в шаре |x| < 1 задана функция
1, если |x| < 1, x2 > 0, f(x1, x2) = − | |
1, если x < 1, x2 < 0.
Доказать, что f(x1, x2) имеет о.п. первого порядка в каждом из полукругов, но не имеет о.п. по x2 в круге |x| < 1.
59
10.6. Вычислить производные первого и второго порядков следующих функций 1) y = |x| sin x; 2) y = |x| cos x в области |x| ≤ α, α R.
Доказать утверждения:
10.7. Если в области Ω у функции f(x) существует о.п. Dαf = ω(x), а у функции ω(x) существует о.п. Dβω, то существует о.п. Dα+βf.
10.8. а) y = signx 6 H1(−1, 1), б) y = |x| H1(−1, 1), y = |x| 6 H2(−1, 1).
◦
10.9. Если f H1(Ω) и g H1 (Ω), то для всех i = 1, 2, . . . , m, справедли-
RR
ва формула fgxi dx = − gfxi dx (формула интегрирования по частям).
Ω Ω
10.10. Если f H1(Ω) и g H1(Ω), то для всех i = 1, 2, . . . , m, справедлива формула
Z |
fgxi dx = − Z |
gfxi dx + Z |
fg cos(n, xi) ds, |
Ω |
Ω |
∂Ω |
|
где под знаком интеграла по границе ∂Ω стоят следы функций f и g на
∂Ω.
◦
10.11. Для любой f(x) H1 (a, b) имеет место неравенство (одномерный вариант неравенства Стеклова (Пуанкаре - Фридрихса))
b |
|
|
b |
Za |
f2 dx ≤ (b − a)2 |
Za |
f02 dx. |
10.12. Доказать существование такой постоянной c > 0, что для любой
◦
f H1 (Ω) имеет место неравенство Стеклова (Пуанкаре - Фридрихса)
|
Z |
Z |
|
|
|
|
f2 dx ≤ c |rf|2 dx. |
|
Ω |
Ω |
|
◦ |
R |
||
10.13. Показать, что выражение (rf, rg) dx задает скалярное произведе- |
|||
|
|
|
Ω |
|
|
|
R |
ние в H1 (Ω), эквивалентное скалярному произведению [fg+(rf, rg)] dx. |
|||
|
|
|
Ω |
10.14. Пусть p, q C(Ω), |
p(x) ≥ p0 > 0, q(x) ≥ 0. Доказать, что |
||
|
|
|
◦ |
скалярные произведения в H1 (Ω)
Z
(f, g) = [fg + (rf, rg)] dx,
Ω
60
