
- •Лекция 3 математическое моделирование
- •3.1 Основные понятия
- •Классификация математических моделей.
- •3.2 Общие принципы математического моделирования
- •3.3 Математическая модель элемента системы
- •3.4 Математическая модель взаимодействия элементов системы
- •3.5 Подобие
- •3.6 Степенные комплексы
- •1. Число простых степенных комплексов, образованных из некоторых величин, не может превзойти числа этих величин.
- •2. Любую функцию некоторых величин можно представить в виде функции степенных комплексов этих величин. В любом выражении вида
- •3.7 Подобие в общем случае
- •3.8 Дополнительные условия подобия
- •3.12.2 Системы массового обслуживания
3.7 Подобие в общем случае
Пусть объекты описываются уравнениями (3.1) – (3.2): два объекта подобны, если
- они имеют сходственные математические описания:
 (3.1)
(3.1)
 ,
(3.2)
,
(3.2)
где
 ;
y1,
y2
и x1i,
x2i
– соответственно неизвестные и заданные
функции независимых переменных t1j
и t2j;
;
y1,
y2
и x1i,
x2i
– соответственно неизвестные и заданные
функции независимых переменных t1j
и t2j;
- сходственные переменные, содержащиеся в математических описаниях, связаны постоянными коэффициентами пропорциональности, которые называют масштабами (константами) подобия
 .
(3.3)
.
(3.3)
При этом остаются в силе и три необходимых условия подобия. Как и ранее, масштабные уравнения можно вывести двумя способами.
Способ подстановки [леб 2-4, 19] основан на преобразовании одного уравнения в другое. Если система уравнений (3.1) – (3.3) непротиворечива, то каждое сходственное уравнение можно решить двумя путями: прямым и косвенным (схемы на рис. 3.10, аналогичные рис. 3.9).

Рисунок 3.10 – Пути решения уравнений (3.1) и (3.2)
Прямой
путь определения неизвестной функции
 (рис. 3.4а) заключается в непосредственном
решении уравнения (3.1), косвенный
– в замене переменных уравнения (3.2)
переменными уравнения (3.1) согласно
(3.3) и решении уравнения
(рис. 3.4а) заключается в непосредственном
решении уравнения (3.1), косвенный
– в замене переменных уравнения (3.2)
переменными уравнения (3.1) согласно
(3.3) и решении уравнения
 (3.1*)
(3.1*)
Зам
переменных
 ,
,
 ,
,
 сходственными переменными
сходственными переменными
 ,
,
 ,
,
 выполняется согласно соотношениям
(3.3). С помощью тех же масштабов
выполняется согласно соотношениям
(3.3). С помощью тех же масштабов
 ,
,
 ,
,
 осуществляется замена производных
сходственных величин. Масштабы связывают
все возможные значения
осуществляется замена производных
сходственных величин. Масштабы связывают
все возможные значения
 ,
,
 ,
,
 и соответствующие им значения
и соответствующие им значения
 ,
,
 ,
,
 ,
в том числе и бесконечно малые приращения,
т.е. дифференциалы
,
в том числе и бесконечно малые приращения,
т.е. дифференциалы
 .
.
Для
замены производной
 сходственной производной
сходственной производной
 находим отношение
находим отношение
 (3.34)
(3.34)
откуда
 .
(3.35)
.
(3.35)
Эти
же выражения можно получить проще. Так
как,
 ,
то
,
то
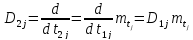 ,
,
откуда
 ,
(3.36)
,
(3.36)
что
позволяет рассматривать операторы
 ,
,
 как сходственные величины, связанные
масштабами
как сходственные величины, связанные
масштабами
 .
.
В
таком случае производную
 можно рассматривать как обычное
произведение и заменять
можно рассматривать как обычное
произведение и заменять
 на
на
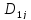 и
и
 на
на
 раздельно с помощью масштабов
раздельно с помощью масштабов
 и
и
 .
При этом согласно (3.35)
.
При этом согласно (3.35)
 .
Аналогично вторую производную
.
Аналогично вторую производную
 можно заменять сходственной второй
производной
можно заменять сходственной второй
производной


и т.д. Все сказанное легко распространить на частные и смешанные производные.
Т.о., при замене переменных одного уравнения сходственными переменными другого в качестве переменных формально можно рассматривать любые операторы дифференцирования.
После
замены переменных
 ,
,
 ,
,
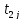 ,
,
 переменными
переменными
 ,
,
 ,
,
 ,
,
 уравнение (3.2) приводят к виду (3.1*),
отличающееся от (3.1) только постоянными
коэффициентами.
уравнение (3.2) приводят к виду (3.1*),
отличающееся от (3.1) только постоянными
коэффициентами.
В
случае подобия решения
 и
и
 уравнений (3.1) и (3.1*) тождественны
уравнений (3.1) и (3.1*) тождественны
 .
.
Прямой
путь определения неизвестной функции
 (рис. 3.4б) состоит в решении (3.2), косвенный
– в замене переменных
(рис. 3.4б) состоит в решении (3.2), косвенный
– в замене переменных
 ,
,
 ,
,
 ,
,
 уравнения (3.1) переменными
уравнения (3.1) переменными
 ,
,
 ,
,
 ,
,
 согласно (3.3), (3.36) и решении уравнения
согласно (3.3), (3.36) и решении уравнения
 (3.2*)
(3.2*)
В
случае подобия решения
 и
и
 уравнений (3.2) и (3.2*) тождественны:
уравнений (3.2) и (3.2*) тождественны:
 .
.
Пример. Даны сходственные уравнения
 (3.37)
(3.37)
 (3.38)
(3.38)
Три пары сходственных переменных связаны масштабами
 .
.
Прямое решение уравнения (3.37) имеет вид
 .
.
Заменой
переменных в (3.38)
 ,
,
 ,
,
 переменными
переменными
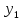 ,
,
 ,
,
 находим косвенное решение уравнения
(3.37) как решение уравнения
находим косвенное решение уравнения
(3.37) как решение уравнения
 (3.37*)
(3.37*)
в виде
 .
.
Для
тождественности решений
 и
и
 необходимо выполнение условий
необходимо выполнение условий

или
 (3.39)
(3.39)
которые
в данном случае представляют собой
масштабные уравнения. Масштаб
 определяется однозначно. Один из
масштабов
определяется однозначно. Один из
масштабов
 можно выбрать произвольно.
можно выбрать произвольно.
Для
выполнения условия
 можно не прибегать к аналитическому
решению уравнений (3.1) и (3.1*), что не всегда
возможно. для этого достаточно сделать
уравнения (3.1) и (3.1*) равносильными,
приравняв их сходственные коэффициенты.
Однако в общем случае эти коэффициенты
обладают различными размерностями.
Поэтому необходимо предварительно
преобразовать (рис. 3.4а) уравнение (3.1*)
в уравнение
можно не прибегать к аналитическому
решению уравнений (3.1) и (3.1*), что не всегда
возможно. для этого достаточно сделать
уравнения (3.1) и (3.1*) равносильными,
приравняв их сходственные коэффициенты.
Однако в общем случае эти коэффициенты
обладают различными размерностями.
Поэтому необходимо предварительно
преобразовать (рис. 3.4а) уравнение (3.1*)
в уравнение
 (3.1**)
(3.1**)
так,
чтобы размерности сходственных
коэффициентов (3.1**) и (3.1) были одинаковы:
[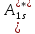 ]
= [
]
= [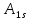 ].
Условия равенства
].
Условия равенства
 получаются в виде
получаются в виде
 =
=
 .
.
Пример.
Для вывода условий равенства уравнения
(3.37) в предыдущем примере умножим
уравнение (3.37*) на
 :
:
 .
.
Размерности
сходственных коэффициентов (3.37) и (3.37*)
равны. Для тождественности решений
 и
и
 необходимо выполнить условия
необходимо выполнить условия

равносильные условиям (3.39).
Если в частном случае, размерности сходственных коэффициентов уравнений (3.37) и (3.37*) одинаковы, то приравнивая их, получаем
 .
.
Такая система уравнений определяет все три масштаба однозначно.
Пример. Даны сходственные уравнения
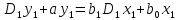 (3.40)
(3.40)
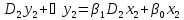 (3.41)
(3.41)
где
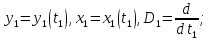

Масштабы равны
 .
.
Замена переменных в (3.41) дает
 (3.40*)
(3.40*)
Так
как сходственные постоянные коэффициенты
в (3.40) и (3.40*) в общем случае различны по
размерностям, то, умножив (3.40*) на
 ,
получим
,
получим
 (3.40**)
(3.40**)
Размерности сходственных постоянных коэффициентов уравнений (3.40) и (3.40**) одинаковы. Приравняв сходственные коэффициенты, получим систему масштабных уравнений
 (3.42)
(3.42)
Масштаб
 определяется однозначно. Один из двух
других масштабов
определяется однозначно. Один из двух
других масштабов
 или
или
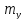 может быть выбран произвольно, если два
последних уравнения совместны.
может быть выбран произвольно, если два
последних уравнения совместны.
Переход
от (3.40*) к (3.40**) означает приведение
размерностей членов (3.40*) к размерностям
членов (3.40). Уравнение размерностей
может быть получено не только таким
способом, но и, например, умножением
(3.40*) на
 .
При этом
.
При этом
 (3.40***)
(3.40***)
Приравняв сходственные коэффициенты уравнений (3.40***) и (3.40), получим систему масштабных уравнений
 (3.43)
(3.43)
отличную от системы (3.42), но легко преобразуемую в нее. Системы (3.42) и (3.43) равносильны.
Совершенно аналогично получают масштабные уравнения из условий тождественности (3.2) и (3.2*).
Таким образом, сущность способа подстановки состоит:
- замена переменных в одном из сходственных уравнений сходственными переменными второго уравнения с помощью масштабов;
- обеспечение тождественности промежуточного уравнения и второго сходственного уравнения;
- получение масштабных уравнений, как условия тождественности указанных двух уравнений.
Способ критериев подобия основан на представлении уравнений в безразмерной форме. Сходственные функции уравнений (3.1) и (3.2) представляются произведениями размерных степенных комплексов и безразмерных функций


После сокращения степенных комплексов уравнения (3.1) и (3.2) оказываются в безразмерной форме
 (3.1б)
(3.1б)
 (3.2б)
(3.2б)
где
[ ]
= 1. Под знаками безразмерных функций
]
= 1. Под знаками безразмерных функций
 величины
величины
 и
и
 объединяются в безразмерные степенные
комплексы – критерии подобия (см. выше)
объединяются в безразмерные степенные
комплексы – критерии подобия (см. выше)
 (3.44)
(3.44)
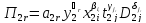 .
(3.45)
.
(3.45)
Следует учесть, что это сокращенная запись критериев подобия. В развернутом виде выражение r-критериев подобия более сложное

причем
в общем случае постоянный множитель
 – степенной комплекс, образованный
постоянными коэффициентами
– степенной комплекс, образованный
постоянными коэффициентами
 .
При этом функции
.
При этом функции
 уравнений (3.1б) и (3.2б) представляются
функциями критериев подобия
уравнений (3.1б) и (3.2б) представляются
функциями критериев подобия
 и
и

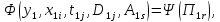

В результате безразмерные уравнения (3.1б) и (3.2б) принимают критериальную форму
 (3.1к)
(3.1к)
 (3.2к)
(3.2к)
Заменив,
согласно первому способу вывода
масштабных уравнений переменные
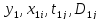 в скрытом виде содержащиеся в (3.1к),
переменными
в скрытом виде содержащиеся в (3.1к),
переменными
 ,
получим
,
получим

Подставив это выражение в (3.1к), имеем
 (3.2к*)
(3.2к*)
В соответствии с первым способом, уравнения (3.2к) и (3.2к*) должны быть тождественны. Для этого необходимо выполнение условия
 (3.46)
(3.46)
представляющего масштабное уравнение в общем виде.
На основании (3.3), (3.46) получаем
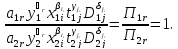 (3.47)
(3.47)
Таким образом, в случае подобия уравнений (3.1) и (3.2) соответствующие им сходственные критерии подобия должны быть равны
 (3.48)
(3.48)
Пример. Пусть заданы уравнения (3.37), (3.38).
 (3.37)
(3.37)
 (3.38)
(3.38)
В безразмерной форме они имеют вид

а в критериальной

где


Масштабные уравнения
 ,
,

тождественны (3.39)
Таким образом, сущность способа критериев подобия состоит в следующем:
- сходственным уравнениям придается безразмерная форма;
- определяются критерии подобия;
- масштабные уравнения получаются приравниванием единице отношений сходственных критериев. Формы масштабных уравнений аналогичны формам соответствующих критериев подобия.
Способ подстановки отличается естественностью и наглядностью, но несколько сложен. Способ критериев подобия носит более формальный характер, но значительно проще в практическом применении.
