3.5 Подобие

Сходство объектов по их математическому описанию (математическая аналогия) при определенных условиях превращается в математическое подобие или просто подобие. Подобие – это полная математическая аналогия при наличии пропорциональности между сходственными переменными, неизменно сохраняющаяся при всех возможных значениях этих переменных, удовлетворяющих сходственным уравнениям.

Математическое описание объекта (расчетная модель) может иметь разнообразную форму:

- простейший случай – явная функция, выражающая переменную через ее аргументы x_i: 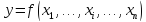или сокращенно , i=1,2,…,n;

- конечное уравнение или сокращенно , i=1,2,…,n, выражающее зависимость в неявной форме;

- обыкновенное дифференциальное уравнение

,

связывающее независимую переменную t, известные функции x_i = x_i(t), неизвестную функцию y = y(t) и производные функций x_i, y. Если ввести оператор дифференцирования , то в символической форме

,

или сокращенно ;

- дифференциальное уравнение в частных производных

,

или сокращенно , где и учтены постоянные коэффициенты A_s.

В общем случае под F можно понимать любой оператор, символизирующий совокупность некоторых действий, выполняемых над y, x_i, t_j, D_j.

Два объекта подобны, если

1. они имеют сходственные математические описания:

(3.1)

, (3.2)

где ; y₁, y₂ и x_1i, x_2i – соответственно неизвестные и заданные функции независимых переменных t_1j и t_2j;

2. сходственные переменные, содержащиеся в математических описаниях, связаны постоянными коэффициентами пропорциональности, которые называют масштабами (константами) подобия

. (3.3)

При условии (3.3) сходственные уравнения и функции, описывающие математические аналоги, а также содержащиеся в них сходственные переменные называются подобными. Подобные функции могут быть изображены в пространстве подобных переменных одной и той же кривой или поверхностью.

Пример. Сходственные функции подобны, если

При этих условиях для них справедлива зависимость на рис. 3.7а. Если принять 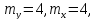то сходственные функции 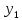, не будут подобными и их графические изображения не совпадают (рис. 3.7б).

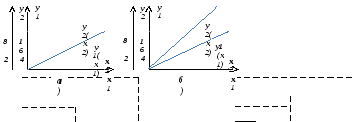
Рисунок 3.7 – Сходственные функции при наличии (а)

и при отсутствии (б) подобия

Особыми частными случаями являются геометрическое, физическое и временное подобие.

Геометрическое подобие – это подобие геометрических образов: точек, линий, поверхностей, фигур, тел. В теории моделирования понимается в более широком смысле, чем принято обычно. Два образа геометрически подобны в широком смысле, если при соответствующем расположении этих образов в некоторой системе координат подобны их математические описания. При этом масштабы, связывающие различные, но однородные по размерности координаты точек геометрических объектов (например, линейные координаты), могут быть одинаковы (равномерное, обычное подобие) и различными (неравномерное подобие) по величине.

Физическое подобие означает подобие физически однородных объектов. Все масштабы являются при этом безразмерными величинами. Временное подобие – подобие функций времени.

Пример. Имеются два генератора переменного тока. Их описывают функции, выражающие напряжения в зависимости от времени t. Для первого генератора , для второго , причем [u] = B, [t] = c. Чтобы записать выражения для масштабов, представим эти уравнения в виде , . Тогда

Различное обозначение напряжений различных генераторов вполне естественно. Различное обозначение t₁, t₂ одной той же величины – времени – имеет на первый взгляд чисто формальный характер. Можно формально считать их «различными» т.к. они входят в разные формулы. Что тогда означает m_t?

Если считать t₁, t₂ такие различные значения одной и той же независимой переменной t, при которой фиксируются значения различных зависимых переменных u₁(t) и u₂(t).

Физическое и временное подобие имеет место (рис. 3.8) при m_u = 10, m_t = 2. Масштаб m_u показывает отношение амплитуд напряжений u₁ и u₂, масштаб m_t - отношение периодов T₁ = 4c и T₂ = 2c.

Рисунок 3.8 – Подобные синусоидальные напряжения

В общем случае временного подобия безразмерный масштаб времени представляет отношение сходственных временных интервалов, которым соответствует неизменное отношение значений или приращений подобных временных функций. В частности, временной масштаб показывает, в каком отношении находятся временные параметры подобных временных функций τ₁ и τ₂, представляющие, например, периоды колебаний (рис. 3.8), постоянные времени, длительности переходных процессов, временные задержки и т.д.

В теории и практике подобие имеет большее значение, чем аналогия. При аналогии двух объектов распространение свойств одного на другой носит характер предположения и нуждается в проверке. При подобии двух объектов знание поведения одного из них означает знание поведения другого.